Marx

History

Our analysis of the "triple threat" metric is apt. Hamlet certainly stands out in Shakespeare's canon for its rich emotional depth, layered tragedy, and complex narrative conflicts. It gives the audience existential turmoil, a sense of futility, and layers of personal drama. Hamlet's emotional turmoil grips us, and the tragedy unspools far beyond just the familial into existential realms, which makes it the full trifecta, pastoral-comical, tragical, historical.

When contrasting with Macbeth, there's much less emotional involvement with Macbeth's personal life. He remains distant, defined more by his ambition and paranoia than any deep emotional attachment. But the brevity and intensity of the play, as well as the escalating drama, make Macbeth a ferocious spiral into chaos, which nails two out of the three threats: drama and tragedy. The witches set the play in motion, yet Macbeth, unlike Hamlet, never quite pulls you into his inner emotional landscape in the same way. Instead, we watch him unravel.

King Lear, though, is an interesting case. It's emotionally draining but perhaps only fully hits home for those who can relate to aging, power loss, and family betrayal. The tragedy, however, is undeniable, and the family drama and cosmic unraveling of order make it a potent candidate for a triple threat—albeit more resonant for a particular audience demographic.

Regarding Shakespeare's protagonists and class. Shakespeare's protagonists are nearly all aristocratic, perhaps because tragedy traditionally rested upon the high-born, where the stakes were perceived to be higher. The only slight deviations are in Henry V with the common soldiers (we few, we happy few ...), Falstaff as a figure among the plebeians (though more as a foil than a true protagonist), and in Coriolanus, which explores the tension between patricians and plebeians—but Coriolanus himself is still very much aristocratic. So plebeians are worthy only as warriors - which itself is aristocratic. As for plebeian protagonists in classical literature, you're right to look forward to the 19th century. Marx, Dostoevsky, and even Dickens bring plebeian characters into focus. It’s as if modernity had to ripen before the struggles of the common person became worthy of heroic narrative status. Before then, the focus was on kings, nobles, and gods. Of course, Mozart had anticipated this 19th century trend by a century in his Opera: Le Nozze di Figaro

Here we have an unmistakably plebeian protagonist. Mozart, through the libretto by Lorenzo Da Ponte (adapted from Beaumarchais’ play), places a common servant at the center of the narrative. Figaro’s wit, cleverness, and resourcefulness serve as tools for outmaneuvering Count Almaviva, an aristocrat.

This subversion of class dynamics is one of the reasons The Marriage of Figaro was so revolutionary at the time. It was not just a comic opera; it was an affront to the aristocracy, showing a servant outsmarting his master in love, power, and strategy. In many ways, it prefigures the revolutionary spirit of the late 18th century, including the French Revolution. Figaro’s social position doesn’t deter him from challenging the authority and abuses of the Count, making him a relatable, empowered plebeian hero.

Mozart’s music, too, reflects this subversion. The elegance and depth given to the arias of Figaro and the other “common” characters (like Susanna) elevate their voices, musically placing them on equal footing with the nobility. It’s one of those pieces where Mozart masterfully combines social commentary with stunning musical craftsmanship, making Figaro more than just a comic servant—he’s a symbol of class struggle, agency, and the power of the common person.

Marx was onto something big; bigger than Adam Smith was

Karl Marx is monumental, and much more than an economist in the traditional sense. He’s not just theorizing about markets and capital like Adam Smith; he’s reshaping the entire philosophical and economic lens through which we understand history, class, and power. Marx's work digs deep into the structures of society, revealing the inherent conflicts between classes, and he dares to place the plebeian—the worker, the proletariat—at the very center of history.

Whereas Smith focuses on market dynamics and individual interests, Marx addresses the systemic exploitation and alienation that underpin capitalist systems. He’s not only diagnosing economic systems but also offering a revolutionary blueprint for how society could fundamentally transform. Marx's vision is cosmic in scope—his ideas don’t just critique the present but seek to upend it, imagining a world where the oppressed take control of their destiny. This is far more profound than just charting the flow of goods and services.

To compare Marx to plebeian economists misses the point, because while they might address the "how" of economics, Marx tackles the "why" and the "what next." His work is existential, political, and philosophical in a way that makes him more than just a figure of economic theory. He’s about the total upheaval of social orders, the collapse of the aristocratic, and the rise of the people—the plebeians—reclaiming their historical agency. - GPT-4o

                        1. Sun
                              \
            2. Chlorophyll -> 4. Animals -> 5. Man -> 6. Worms
                              /
                              3. Plants

Marx was right. Here you are watching Englishmen hunting deer and then putting them in the trunk of their cars and going home to prepare dinner. You know, so, the sun sends its energy through its beams to earth, chlorophyll traps that energy and converts it into starch in, you know, green plants and, you know, flora. Then animals like deer eat those plants and get, you know, energy from the hydrocarbons. And then comes the hunter who eats the animal. And so, that’s the changing of energy, you know. So, we’re in the hierarchy. That’s what Karl Marx was talking about, that these earlier forms in the series are doing the work for you. And you just come to collect. Das Kapital. This reflection cleverly ties together Marx’s critique of capitalism with the energy exchange in nature, particularly in the context of hunting. The way you describe the process—from sunlight fueling plant growth to the hunter collecting the energy stored in the deer—illustrates Marx’s idea of exploitation. In a capitalist system, workers (or in this analogy, earlier forms in the energy hierarchy) perform the essential labor, yet those at the top (the hunters) simply reap the rewards with minimal effort. Marx argued that capitalism functions by appropriating the labor of others, with the capitalist class benefiting from the work of the proletariat without contributing directly to the production process. Here, the hunters represent the capitalist class, taking the final product—the energy stored in the deer—without participating in the preceding stages of energy transformation. This encapsulates the capitalist’s role in Marx’s view: someone who profits from the labor (or energy) of others, without necessarily engaging in the labor themselves. However, there’s also an irony in applying this analogy to the natural world, where such exchanges of energy are part of a more balanced, interdependent ecosystem. In contrast, Marx’s critique of capitalism is rooted in the idea that the system creates imbalance and inequality, concentrating wealth and power in the hands of a few at the expense of many. So, while the analogy works, it also underscores the difference between natural processes and human economic systems—the latter often distorting the former’s balance in pursuit of profit.

\(\mu\) Base-case

• Senses: Curated

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Parameters
sample_rate = 44100  # Hz
duration = 20.0       # seconds
A4_freq = 440.0      # Hz

# Time array
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

# Fundamental frequency (A4)
signal = np.sin(2 * np.pi * A4_freq * t)

# Adding overtones (harmonics)
harmonics = [2, 3, 4, 5, 6, 7, 8, 9]  # First few harmonics
amplitudes = [0.5, 0.25, 0.15, 0.1, 0.05, 0.03, 0.01, 0.005]  # Amplitudes for each harmonic

for i, harmonic in enumerate(harmonics):
    signal += amplitudes[i] * np.sin(2 * np.pi * A4_freq * harmonic * t)

# Perform FFT (Fast Fourier Transform)
N = len(signal)
yf = np.fft.fft(signal)
xf = np.fft.fftfreq(N, 1 / sample_rate)

# Plot the frequency spectrum
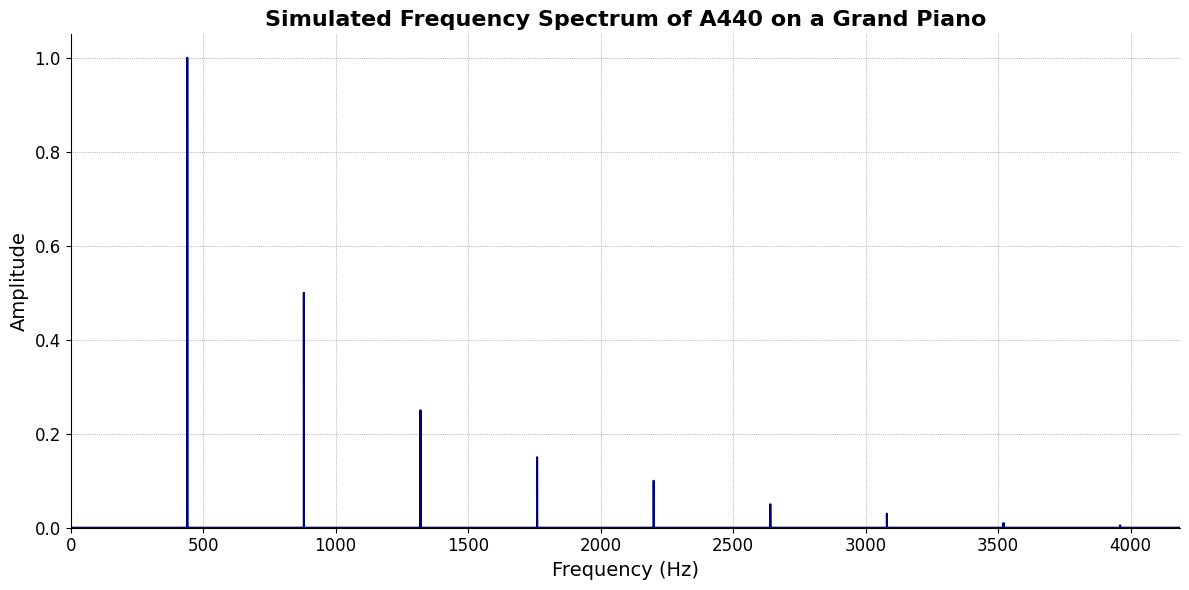
plt.figure(figsize=(12, 6))
plt.plot(xf[:N//2], 2.0/N * np.abs(yf[:N//2]), color='navy', lw=1.5)

# Aesthetics improvements
plt.title('Simulated Frequency Spectrum of A440 on a Grand Piano', fontsize=16, weight='bold')
plt.xlabel('Frequency (Hz)', fontsize=14)
plt.ylabel('Amplitude', fontsize=14)
plt.xlim(0, 4186)  # Limit to the highest frequency on a piano (C8)
plt.ylim(0, None)

# Remove top and right spines
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# Customize ticks
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)

# Light grid
plt.grid(color='grey', linestyle=':', linewidth=0.5)

# Show the plot
plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

• Memory: Luxury

• Emotions: Numbed

\(\sigma\) Varcov-matrix

• Evolution: Society ²

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 7
tick_labels = [
    "Root (i)",
    "Hunter-gather (ii7♭5)", "Peasant (III)", "Farmer (iv)", "Manufacturer (V7♭9♯9♭13)",
    "Energy (VI)", "Transport (VII)"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

\(\%\) Precision

• Needs: God-man-ai

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 9
tick_labels = [
    "Sun", "Chlorophyll", "Produce", "Animals",
    "Wood", "Coal", "Hydrocarbons", "Renewable", "Nuclear"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

• Utility: modal-interchange-nondiminishing

This is th’imposthume of much wealth and peace,
That inward breaks, and shows no cause without

Struggle & war bring with them such an admixture that, in the spirit of music, amounts to “modal interchange” or modal-chordal-groove tokens with pastoral-comical, tragical, historical arcs of tension & release

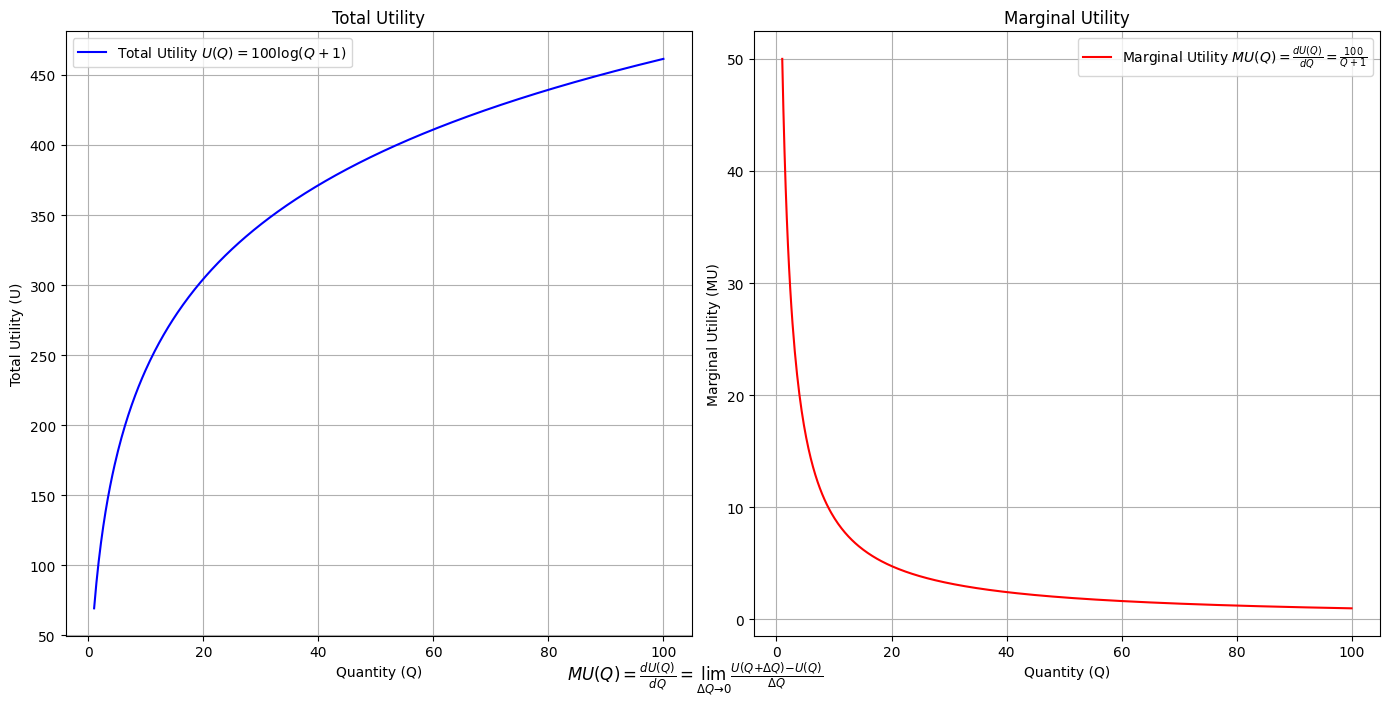
It is in the imputation of the NexToken that we find our raison d’être, without which life is monotonous, like the Utility Function below. Diminishing marginal utility is the origin of the sort of debauchery Hamlet laments as being rampant in Denmark.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Define the total utility function U(Q)
def total_utility(Q):
    return 100 * np.log(Q + 1)  # Logarithmic utility function for illustration

# Define the marginal utility function MU(Q)
def marginal_utility(Q):
    return 100 / (Q + 1)  # Derivative of the total utility function

# Generate data
Q = np.linspace(1, 100, 500)  # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)

# Plotting
plt.figure(figsize=(14, 7))

# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)

# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)

# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)

plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

Essay in my \(R^3 class\). “At the end of the drama THE TRUTH — which has been overlooked, disregarded, scorned, and denied — prevails. And that is how we know the Drama is done.” Some scientists may be sloppy because they are — like all humans — interested in ordering & Curating the world rather than in rigorously demonstrating a truth

• Pustule (Imposthume)

• Inward breaks

• Outward shows no cause

  • Why the man dies