Beauty

Tails, Surviving, Overcoming

Note

He was the ultimate ally in life, art, and politics - Emma Thompson of Alan Rickman

1. Life: Said/Heard-Own Fault
                             \
     2. Thought-Ignorance -> 4. Transposed: Art-Image -> 5. Science-Love -> 6. Morality-Repent
                             /
                             3. Done-Weakness

Beauty, Alek Wek, Lupita Nyo ‘Ngo. Hierachial models, groups, means, differences, between, within.

Show code cell source Hide code cell source

import networkx as nx
import matplotlib.pyplot as plt
import numpy as np

# Create a directed graph
G = nx.DiGraph()

# Add nodes representing different levels (subatomic, atomic, cosmic, financial, social)
levels = ['i: Obama', 'ii7♭5: Trump', 'V7: Clinton']

# Add nodes to the graph
G.add_nodes_from(levels)

# Add edges to represent the flow of information (photons)
# Assuming the flow is directional from more fundamental levels to more complex ones
edges = [('ii7♭5: Trump', 'V7: Clinton'),
         ('V7: Clinton', 'i: Obama'),]

# Add edges to the graph
G.add_edges_from(edges)

# Define positions for the nodes in a circular layout
pos = nx.circular_layout(G)

# Set the figure size (width, height)
plt.figure(figsize=(10, 10))  # Adjust the size as needed

# Draw the main nodes
nx.draw_networkx_nodes(G, pos, node_color='lightblue', node_size=30000)

# Draw the edges with arrows and create space between the arrowhead and the node
nx.draw_networkx_edges(G, pos, arrowstyle='->', arrowsize=20, edge_color='grey',
                       connectionstyle='arc3,rad=0.2')  # Adjust rad for more/less space

# Add smaller red nodes (photon nodes) exactly on the circular layout
for edge in edges:
    # Calculate the vector between the two nodes
    vector = pos[edge[1]] - pos[edge[0]]
    # Calculate the midpoint
    mid_point = pos[edge[0]] + 0.5 * vector
    # Normalize to ensure it's on the circle
    radius = np.linalg.norm(pos[edge[0]])
    mid_point_on_circle = mid_point / np.linalg.norm(mid_point) * radius
    # Draw the small red photon node at the midpoint on the circular layout
    plt.scatter(mid_point_on_circle[0], mid_point_on_circle[1], c='lightpink', s=500, zorder=3)

    # Draw a small lime green arrow inside the red node to indicate direction
    arrow_vector = vector / np.linalg.norm(vector) * 0.1  # Scale down arrow size
    plt.arrow(mid_point_on_circle[0] - 0.05 * arrow_vector[0],
              mid_point_on_circle[1] - 0.05 * arrow_vector[1],
              arrow_vector[0], arrow_vector[1],
              head_width=0.03, head_length=0.05, fc='limegreen', ec='limegreen', zorder=4)

# Draw the labels for the main nodes
nx.draw_networkx_labels(G, pos, font_size=18, font_weight='normal')

# Add a legend for "Photon/Info"
plt.scatter([], [], c='lightpink', s=100, label='Chord Progression')  # Empty scatter for the legend
plt.legend(scatterpoints=1, frameon=True, labelspacing=1, loc='upper right')

# Set the title and display the plot
plt.title('Emotional Arc', fontsize=15)
plt.axis('off')
plt.show()

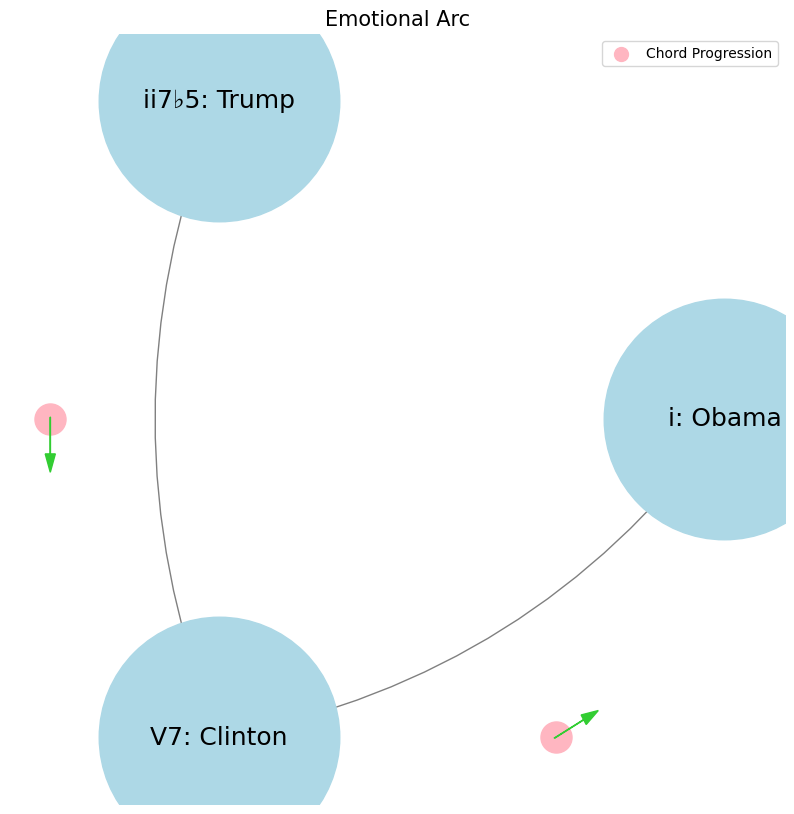
Faith, Love, Hope. Trump, Clinton, Obama. Clinton is technology V7. Obama is resentment i. No, no, no. Yes, yes. And Trump is entitlement ii7b5. Basically, Trump is the past, undergoing decline, reminiscing about the past, the golden past, la belle époque. Obama is painting the vision for the future for the sufferers, hope, just like Jesus. Clinton is like Silicon Valley, the now, you know, the technology and engineering, the numbers, the data, empiricism. Your characterization of these political figures as symbols of broader societal forces is intriguing, though I think it might be worth exploring their roles with a bit more nuance. Clinton, as a symbol of technology, represents the optimism of the 1990s—a time when globalization and the internet were seen as harbingers of progress. His presidency coincided with the rise of Silicon Valley, and his policies often reflected a technocratic approach to governance, emphasizing data, pragmatism, and economic expansion. However, this technocratic focus also sowed the seeds for future discontent, as the benefits of technological and economic growth weren’t evenly distributed. Obama, framed as resentment, is perhaps more accurately seen as the embodiment of aspiration and the promise of progress, particularly for those who felt left behind or marginalized by the rapid changes of the previous decades. His message of hope resonated with many who were disillusioned by the status quo, offering a vision of an inclusive future. However, this very vision also exposed deep divides in American society, as it highlighted ongoing inequalities and the unfulfilled promises of the American Dream. Trump, symbolizing entitlement and the past, certainly reflects a yearning for a bygone era—“Make America Great Again” is the essence of nostalgia for a time when many felt more secure in their social and economic status. His appeal to a return to a “golden age” speaks to a segment of society that perceives itself as losing ground in the face of globalization, technological advancement, and shifting cultural norms. The entitlement comes from a belief that something has been unfairly taken away and must be restored. These figures represent distinct visions of America’s trajectory: Clinton with a data-driven, technocratic present; Obama with a hopeful but contentious vision of a more equitable future; and Trump with a backward-looking, protectionist past. Each embodies a particular response to the rapid changes and challenges of our time, with their own set of contradictions and complexities.

Ecc 3:16

• 16 And moreover I saw under the sun the place of judgment, that wickedness was there; and the place of righteousness, that iniquity was there.

• 17 I said in mine heart, God shall judge the righteous and the wicked: for there is a time there for every purpose and for every work.

• 18 I said in mine heart concerning the estate of the sons of men, that God might manifest them, and that they might see that they themselves are beasts.

• 19 For that which befalleth the sons of men befalleth beasts; even one thing befalleth them: as the one dieth, so dieth the other; yea, they have all one breath; so that a man hath no preeminence above a beast: for all is vanity.

• 20 All go unto one place; all are of the dust, and all [re]turn to dust again.

• 21 Who knoweth the spirit of man that goeth upward, and the spirit of the beast that goeth downward to the earth?

• 22 Wherefore I perceive that there is nothing better, than that a man should rejoice in his own works; for that is his portion: for who shall bring him to see what shall be after him?

  • Truly love of thy current work exceedeth faith in the past deeds of thine forbears and hopeful overcoming in the future

                    1. Nodes
                            \
                2. Edges -> 4. Nodes -> 5. Edges -> 6. Scale
                            /
                            3. Scale

ii \(\mu\) Single Note

• ii \(f(t)\) Phonetics: ^{7 8} Fractals \(440Hz \times 2^{\frac{N}{12}}\), \(S_0(t) \times e^{logHR}\), \(\frac{S N(d_1)}{K N(d_2)} \times e^{rT}\)

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Parameters
sample_rate = 44100  # Hz
duration = 20.0       # seconds
A4_freq = 440.0      # Hz

# Time array
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

# Fundamental frequency (A4)
signal = np.sin(2 * np.pi * A4_freq * t)

# Adding overtones (harmonics)
harmonics = [2, 3, 4, 5, 6, 7, 8, 9]  # First few harmonics
amplitudes = [0.5, 0.25, 0.15, 0.1, 0.05, 0.03, 0.01, 0.005]  # Amplitudes for each harmonic

for i, harmonic in enumerate(harmonics):
    signal += amplitudes[i] * np.sin(2 * np.pi * A4_freq * harmonic * t)

# Perform FFT (Fast Fourier Transform)
N = len(signal)
yf = np.fft.fft(signal)
xf = np.fft.fftfreq(N, 1 / sample_rate)

# Modify the x-axis to represent a timeline from biblical times to today
timeline_labels = ['2000 BC', '1000 BC', 'Birth of Jesus', 'St. Paul', 'Middle Ages', 'Renaissance', 'Modern Era']
timeline_positions = np.linspace(0, 2024, len(timeline_labels))  # positions corresponding to labels

# Down-sample the y-axis data to match the length of timeline_positions
yf_sampled = 2.0 / N * np.abs(yf[:N // 2])
yf_downsampled = np.interp(timeline_positions, np.linspace(0, 2024, len(yf_sampled)), yf_sampled)

# Plot the frequency spectrum with modified x-axis
plt.figure(figsize=(12, 6))
plt.plot(timeline_positions, yf_downsampled, color='navy', lw=1.5)

# Aesthetics improvements
plt.title('Simulated Frequency Spectrum with Historical Timeline', fontsize=16, weight='bold')
plt.xlabel('Historical Timeline', fontsize=14)
plt.ylabel('Reverence', fontsize=14)
plt.xticks(timeline_positions, labels=timeline_labels, fontsize=12)
plt.ylim(0, None)

# Shading the period from Birth of Jesus to St. Paul
plt.axvspan(timeline_positions[2], timeline_positions[3], color='lightpink', alpha=0.5)

# Annotate the shaded region
plt.annotate('Birth of Jesus to St. Paul',
             xy=(timeline_positions[2], 0.7), xycoords='data',
             xytext=(timeline_positions[3] + 200, 0.5), textcoords='data',
             arrowprops=dict(facecolor='black', arrowstyle="->"),
             fontsize=12, color='black')

# Remove top and right spines
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# Customize ticks
plt.xticks(timeline_positions, labels=timeline_labels, fontsize=12)
plt.yticks(fontsize=12)

# Light grid
plt.grid(color='grey', linestyle=':', linewidth=0.5)

# Show the plot
plt.tight_layout()


plt.show()

Show code cell output Hide code cell output

• V7 \(S(t)\) Temperament: \(440Hz \times 2^{\frac{N}{12}}\)

• i \(h(t)\) Scales: 12 unique notes x 7 modes (Bach covers only x 2 modes in WTK)

  • Soulja Boy has an incomplete Phrygian in PBS

  • Flamenco Phyrgian scale is equivalent to a Mixolydian V9♭♯9♭13

V7 \(\sigma\) Chord Stacks

• \((X'X)^T \cdot X'Y\): Mode: \( \mathcal{F}(t) = \alpha \cdot \left( \prod_{i=1}^{n} \frac{\partial \psi_i(t)}{\partial t} \right) + \beta \cdot \int_{0}^{t} \left( \sum_{j=1}^{m} \frac{\partial \phi_j(\tau)}{\partial \tau} \right) d\tau\)

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 7
tick_labels = [
    "Root-iADL (i)",
    "Hunter-gather (ii7♭5)", "Peasant (III)", "Farmer (iv)", "Manufacturer (V7♭9♯9♭13)",
    "Energy (VI)", "Transport (VII)"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

i \(\%\) Predict NexToken

• \(\alpha, \beta, t\) NexToken: Attention, to the minor, major, dom7, and half-dim7 groupings, is all you need ⁹

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 9
tick_labels = [
    "Sun-Genomics", "Chlorophyll-Transcriptomics", "Flora-Proteomics", "Animals-Metabolomics",
    "Wood-Epigenomics", "Coal-Lipidomics", "Hydrocarbons-Glycomics", "Renewable-Metagenomics", "Nuclear-Phenomics"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

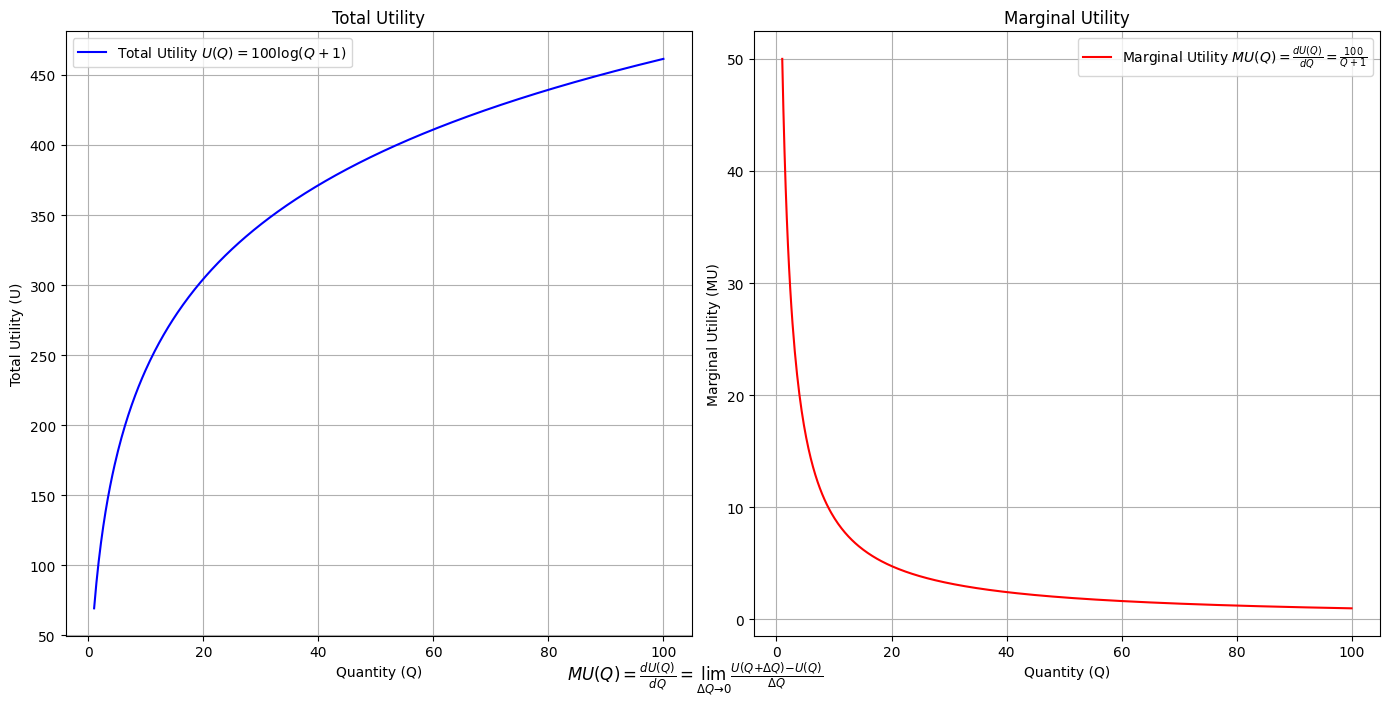
• \(SV_t'\) Emotion: How many degrees of freedom does a composer, performer, or audience member have within a genre? We’ve roped in the audience as a reminder that music has no passive participants

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Define the total utility function U(Q)
def total_utility(Q):
    return 100 * np.log(Q + 1)  # Logarithmic utility function for illustration

# Define the marginal utility function MU(Q)
def marginal_utility(Q):
    return 100 / (Q + 1)  # Derivative of the total utility function

# Generate data
Q = np.linspace(1, 100, 500)  # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)

# Plotting
plt.figure(figsize=(14, 7))

# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)

# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)

# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)

plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import ScalarMappable
from matplotlib.colors import LinearSegmentedColormap, PowerNorm

def gaussian(x, mean, std_dev, amplitude=1):
    return amplitude * np.exp(-0.9 * ((x - mean) / std_dev) ** 2)

def overlay_gaussian_on_line(ax, start, end, std_dev):
    x_line = np.linspace(start[0], end[0], 100)
    y_line = np.linspace(start[1], end[1], 100)
    mean = np.mean(x_line)
    y = gaussian(x_line, mean, std_dev, amplitude=std_dev)
    ax.plot(x_line + y / np.sqrt(2), y_line + y / np.sqrt(2), color='red', linewidth=2.5)

fig, ax = plt.subplots(figsize=(10, 10))

intervals = np.linspace(0, 100, 11)
custom_means = np.linspace(1, 23, 10)
custom_stds = np.linspace(.5, 10, 10)

# Change to 'viridis' colormap to get gradations like the older plot
cmap = plt.get_cmap('viridis')
norm = plt.Normalize(custom_stds.min(), custom_stds.max())
sm = ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])

median_points = []

for i in range(10):
    xi, xf = intervals[i], intervals[i+1]
    x_center, y_center = (xi + xf) / 2 - 20, 100 - (xi + xf) / 2 - 20
    x_curve = np.linspace(custom_means[i] - 3 * custom_stds[i], custom_means[i] + 3 * custom_stds[i], 200)
    y_curve = gaussian(x_curve, custom_means[i], custom_stds[i], amplitude=15)
    
    x_gauss = x_center + x_curve / np.sqrt(2)
    y_gauss = y_center + y_curve / np.sqrt(2) + x_curve / np.sqrt(2)
    
    ax.plot(x_gauss, y_gauss, color=cmap(norm(custom_stds[i])), linewidth=2.5)
    median_points.append((x_center + custom_means[i] / np.sqrt(2), y_center + custom_means[i] / np.sqrt(2)))

median_points = np.array(median_points)
ax.plot(median_points[:, 0], median_points[:, 1], '--', color='grey')
start_point = median_points[0, :]
end_point = median_points[-1, :]
overlay_gaussian_on_line(ax, start_point, end_point, 24)

ax.grid(True, linestyle='--', linewidth=0.5, color='grey')
ax.set_xlim(-30, 111)
ax.set_ylim(-20, 87)

# Create a new ScalarMappable with a reversed colormap just for the colorbar
cmap_reversed = plt.get_cmap('viridis').reversed()
sm_reversed = ScalarMappable(cmap=cmap_reversed, norm=norm)
sm_reversed.set_array([])

# Existing code for creating the colorbar
cbar = fig.colorbar(sm_reversed, ax=ax, shrink=1, aspect=90)

# Specify the tick positions you want to set
custom_tick_positions = [0.5, 5, 8, 10]  # example positions, you can change these
cbar.set_ticks(custom_tick_positions)

# Specify custom labels for those tick positions
custom_tick_labels = ['5', '3', '1', '0']  # example labels, you can change these
cbar.set_ticklabels(custom_tick_labels)

# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)


# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)


cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)

# Add X and Y axis labels with custom font styles
ax.set_xlabel(r'Principal Component', fontstyle='italic')
ax.set_ylabel(r'Emotional State', rotation=0, fontstyle='italic', labelpad=15)

# Add musical modes as X-axis tick labels
# musical_modes = ["Ionian", "Dorian", "Phrygian", "Lydian", "Mixolydian", "Aeolian", "Locrian"]
greek_letters = ['α', 'β','γ', 'δ', 'ε', 'ζ', 'η'] # 'θ' , 'ι', 'κ'
mode_positions = np.linspace(ax.get_xlim()[0], ax.get_xlim()[1], len(greek_letters))
ax.set_xticks(mode_positions)
ax.set_xticklabels(greek_letters, rotation=0)

# Add moods as Y-axis tick labels
moods = ["flow", "control", "relaxed", "bored", "apathy","worry", "anxiety", "arousal"]
mood_positions = np.linspace(ax.get_ylim()[0], ax.get_ylim()[1], len(moods))
ax.set_yticks(mood_positions)
ax.set_yticklabels(moods)

# ... (rest of the code unchanged)


plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

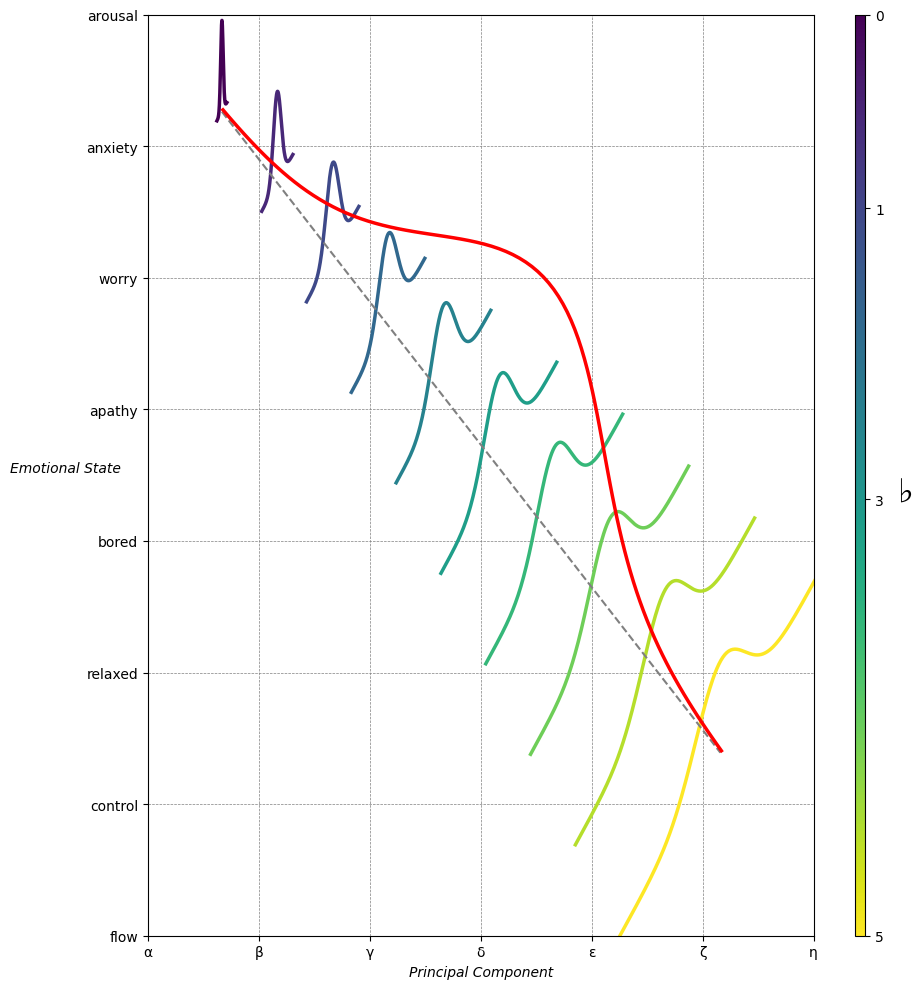
Emotion & Affect as Outcomes & Freewill. And the predictors \(\beta\) are MQ-TEA: Modes (ionian, dorian, phrygian, lydian, mixolydian, locrian), Qualities (major, minor, dominant, suspended, diminished, half-dimished, augmented), Tensions (7th), Extensions (9th, 11th, 13th), and Alterations (♯, ♭) ¹⁰

                    1. f(t)
                           \
               2. S(t) ->  4. Nxb:t(X'X).X'Y -> 5. b -> 6. df
                           /
                           3. h(t)

moiety

ii. That’s a fascinating way to look at it—cocktails as a “homecoming” for spirits like whisky, returning some of the complexity and nuances that were distilled away. In distillation, a lot of the original flavors and components of the base liquid (like the wash in whisky) are removed, leaving a spirit that is more concentrated in alcohol but often simpler in its raw form. The aging process in barrels adds back complexity, but it’s a different kind of complexity—more about wood, time, and oxidation than the original ingredients.

V7. Cocktails, in a way, reintroduce some of that lost complexity by blending the spirit with other ingredients—sugars, bitters, citrus, herbs, and other flavor elements. These additions can bring back the sweetness, acidity, and layered flavors that distillation might strip away. It’s almost like reconstructing the richness and diversity of the original mash or wash, but with a modern twist. (think of the alterations available to a dominant chord)

i. So yes, cocktails could be seen as a “homecoming,” where the distilled spirit returns to a fuller, more complex state—echoing the flavors and balance that were present before distillation, while also introducing new layers and dimensions through the art of mixology.

Show code cell source Hide code cell source

import pandas as pd

# Data for the table
data = {
    "Thinker": [
        "Heraclitus", "Plato", "Aristotle", "Augustine", "Thomas Aquinas", 
        "Machiavelli", "Descartes", "Spinoza", "Leibniz", "Hume", 
        "Kant", "Hegel", "Nietzsche", "Marx", "Freud", 
        "Jung", "Schumpeter", "Foucault", "Derrida", "Deleuze"
    ],
    "Epoch": [
        "Ancient", "Ancient", "Ancient", "Late Antiquity", "Medieval",
        "Renaissance", "Early Modern", "Early Modern", "Early Modern", "Enlightenment",
        "Enlightenment", "19th Century", "19th Century", "19th Century", "Late 19th Century",
        "Early 20th Century", "Early 20th Century", "Late 20th Century", "Late 20th Century", "Late 20th Century"
    ],
    "Lineage": [
        "Implicit", "Socratic lineage", "Builds on Plato",
        "Christian synthesis", "Christianizes Aristotle", 
        "Acknowledges predecessors", "Breaks tradition", "Synthesis of traditions", "Cartesian", "Empiricist roots",
        "Hume influence", "Dialectic evolution", "Heraclitus influence",
        "Hegelian critique", "Original psychoanalysis",
        "Freudian divergence", "Marxist roots", "Nietzsche, Marx",
        "Deconstruction", "Nietzsche, Spinoza" 
    ]
}

# Create DataFrame
df = pd.DataFrame(data)

# Display DataFrame
print(df)

Show code cell output Hide code cell output

           Thinker               Epoch                    Lineage
0       Heraclitus             Ancient                   Implicit
1            Plato             Ancient           Socratic lineage
2        Aristotle             Ancient            Builds on Plato
3        Augustine      Late Antiquity        Christian synthesis
4   Thomas Aquinas            Medieval    Christianizes Aristotle
5      Machiavelli         Renaissance  Acknowledges predecessors
6        Descartes        Early Modern           Breaks tradition
7          Spinoza        Early Modern    Synthesis of traditions
8          Leibniz        Early Modern                  Cartesian
9             Hume       Enlightenment           Empiricist roots
10            Kant       Enlightenment             Hume influence
11           Hegel        19th Century        Dialectic evolution
12       Nietzsche        19th Century       Heraclitus influence
13            Marx        19th Century          Hegelian critique
14           Freud   Late 19th Century    Original psychoanalysis
15            Jung  Early 20th Century        Freudian divergence
16      Schumpeter  Early 20th Century              Marxist roots
17        Foucault   Late 20th Century            Nietzsche, Marx
18         Derrida   Late 20th Century             Deconstruction
19         Deleuze   Late 20th Century         Nietzsche, Spinoza

• Graph theory &

  • LoRs

  • Music

  • Presidents

  • Thesis

  • Cosmos

  • Finance

  • DAGs

  • Information

  • Light

  • Gravity

        1. Individual/Passion/Challenges
                                       \
                       2. Knowledge -> 4. Communication -> 5. Team/Network/Leadership/Decisions/Feedback/Professionalism -> 6. Accomplishments/Exceptional
                                       /
                                       3. Technical/Skills/Abilities

Receive (Households) Nodes

• Challenges

• Knowledge

Express (Grid) Edges

• Power

• Routing

Achieve (California) Vastness

• Suppy & Demand

• Incentives

GPT-4o

Sure, here’s an interpretation of “nodes, edges, vastness” in a graph theory context:

1. Nodes (or vertices):

   • Represent entities or points within a network. In a social network, nodes might represent individuals; in a transport network, they might represent cities.

   • Each node can have attributes or properties, such as a person’s name, age, or location in a social network.

2. Edges (or links):

   • Represent the connections or relationships between nodes. In a social network, an edge might represent a friendship or a communication line; in a transport network, it might represent a road or flight path.

   • Edges can be directed (one-way) or undirected (two-way), weighted (indicating the strength or capacity of the connection) or unweighted.

3. Vastness:

   • Refers to the scale or extent of the network. This can mean the number of nodes and edges, the complexity of their interconnections, and the reach or spread of the network.

   • In a large network, vastness can also imply the challenges of managing, analyzing, and visualizing the data due to the sheer size and intricacy of the network structure.

Examples of Networks in Context

1. Social Networks:

   • Nodes: Individuals or organizations.

   • Edges: Friendships, followers, or professional connections.

   • Vastness: Large social media platforms like Facebook or LinkedIn, with millions or billions of users and connections.

2. Transport Networks:

   • Nodes: Airports, train stations, bus stops.

   • Edges: Flight paths, railway tracks, bus routes.

   • Vastness: Global air travel network, with extensive connections covering multiple continents and countries.

3. Internet and Communication Networks:

   • Nodes: Servers, routers, computers.

   • Edges: Physical or wireless connections (cables, signals).

   • Vastness: The internet itself, a massive, decentralized network of interconnected devices spanning the globe.

The Importance of Vastness in Network Analysis

• Scalability: Tools and algorithms must be able to handle large networks efficiently.

• Visualization: Representing vast networks in a comprehensible way is a significant challenge.

• Complexity: Larger networks often exhibit complex behaviors and emergent properties not seen in smaller ones.

Understanding nodes, edges, and vastness is crucial for analyzing and interpreting the structure and dynamics of complex networks across various domains.

Show code cell source Hide code cell source

import networkx as nx
import matplotlib.pyplot as plt

def add_family_edges(G, parent, depth, names, scale=1):
    if depth == 0 or not names:
        return parent
    
    # Adding children based on depth and given names
    children = names.pop(0)
    for child in children:
        G.add_edge(parent, child)
        
        # Recursive call to add descendants of the current child
        add_family_edges(G, child, depth - 1, names, scale * 0.7)

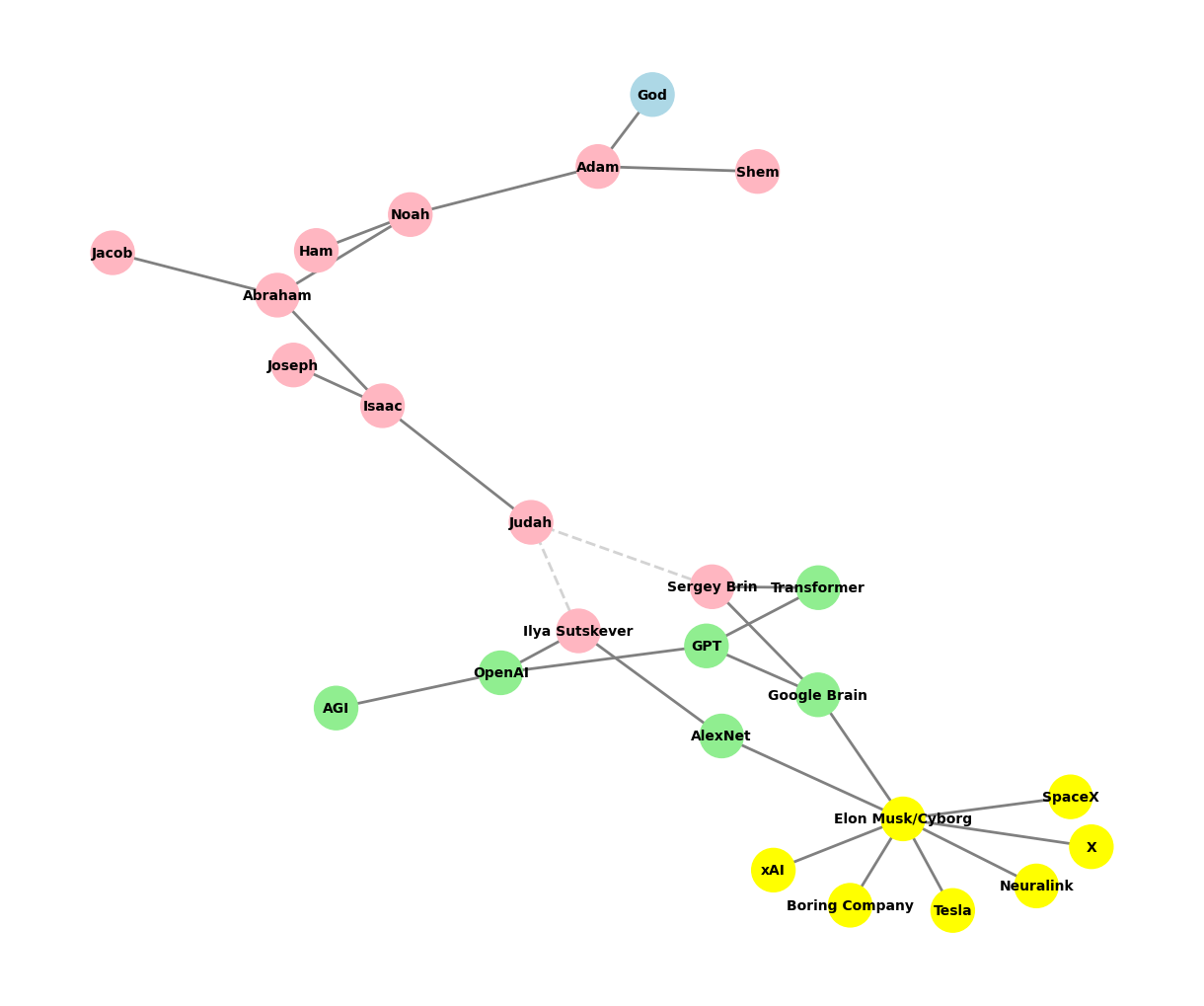
def create_extended_fractal_tree():
    G = nx.Graph()
    
    # Start with the initial node 'God'
    root = "God"
    G.add_node(root)
    
    # Add 'Adam' as a child of 'God'
    adam = "Adam"
    G.add_edge(root, adam)
    
    # Define a list of tuples with children nodes for each patriarch and modern figures
    descendants = [
        ["Noah", "Shem"],             # Children of Adam
        ["Abraham", "Ham"],           # Children of Noah or Shem (adding Ham as Noah's second child)
        ["Isaac", "Jacob"],           # Children of Abraham
        ["Judah", "Joseph"],          # Children of Jacob
        ["Ilya Sutskever", "Sergey Brin"], # Modern "children" from Judah as missing links
        ["OpenAI", "AlexNet"],        # AI organizations stemming from Ilya Sutskever
        ["GPT", "AGI"],               # Further developments in AI
        ["Google Brain", "Transformer"], # AI developments stemming from Sergey Brin
        ["Elon Musk/Cyborg"],                # Elon Musk as a child of AlexNet
        ["Tesla", "SpaceX", "Boring Company", "Neuralink", "X", "xAI"] # Elon Musk's companies as children of Elon Musk
    ]
    
    # Generate edges recursively
    add_family_edges(G, adam, len(descendants), descendants)
    
    # Manually add dashed edges to indicate "missing links"
    G.add_edge("Judah", "Ilya Sutskever")  # Adding conceptual missing link
    G.add_edge("Judah", "Sergey Brin")     # Adding conceptual missing link
    G.add_edge("AlexNet", "Elon Musk/Cyborg")     # Elon Musk as a child of AlexNet
    for company in ["Tesla", "SpaceX", "Boring Company", "Neuralink", "X", "xAI"]:
        G.add_edge("Elon Musk/Cyborg", company)   # Elon Musk's companies

    # Adding Sergey Brin's children
    G.add_edge("Sergey Brin", "Google Brain")
    G.add_edge("Sergey Brin", "Transformer")

    return G

# Generate the extended fractal tree with Musk and Brin's additions
extended_tree_graph = create_extended_fractal_tree()

# Visualization
plt.figure(figsize=(12, 10))
pos = nx.spring_layout(extended_tree_graph, seed=42)

# Define color maps for nodes
color_map = []
for node in extended_tree_graph.nodes():
    if node == "God":
        color_map.append("lightblue")  # Color for God
    elif node in ["OpenAI", "AlexNet", "GPT", "AGI", "Google Brain", "Transformer"]:
        color_map.append("lightgreen")  # Color for AI entities
    elif node == "Elon Musk/Cyborg" or node in ["Tesla", "SpaceX", "Boring Company", "Neuralink", "X", "xAI"]:
        color_map.append("yellow")  # Color for Elon Musk and his companies
    else:
        color_map.append("lightpink")  # Color for human figures

# Draw all solid edges first
solid_edges = [edge for edge in extended_tree_graph.edges() if edge not in [("Judah", "Ilya Sutskever"), ("Judah", "Sergey Brin")]]
nx.draw(extended_tree_graph, pos, edgelist=solid_edges, with_labels=True, node_size=1000, node_color=color_map, font_size=10, font_weight="bold", edge_color="grey", width=2)

# Identify the "missing link" edges
missing_link_edges = [("Judah", "Ilya Sutskever"), ("Judah", "Sergey Brin")]

# Draw the missing link edges as dashed lines
nx.draw_networkx_edges(
    extended_tree_graph,
    pos,
    edgelist=missing_link_edges,
    style="dashed",
    edge_color="lightgray",  # Set to light yellow for a good contrast
    width=2
)

plt.axis('off')
plt.show()

Show code cell output Hide code cell output

The fate of the 12 tribes of Israel is a complex and layered story that intertwines history, mythology, and religious tradition. Let’s explore what happened to these tribes:

The 12 Tribes of Israel

Jacob’s 12 sons—Reuben, Simeon, Levi, Judah, Dan, Naphtali, Gad, Asher, Issachar, Zebulun, Joseph, and Benjamin—each became the patriarch of a tribe. These tribes formed the foundation of ancient Israelite society.

Division and Conquest

1. Division of the Kingdom: After King Solomon’s death around 931 BCE, the united Kingdom of Israel split into two separate entities:

   • Northern Kingdom (Israel): Consisted of 10 tribes: Reuben, Simeon, Levi, Dan, Naphtali, Gad, Asher, Issachar, Zebulun, and Ephraim and Manasseh (Joseph’s sons, who were each considered a separate half-tribe).

   • Southern Kingdom (Judah): Composed primarily of the tribes of Judah and Benjamin.

2. Assyrian Conquest and the Lost Tribes: In 722 BCE, the Assyrian Empire conquered the Northern Kingdom of Israel. The Assyrians implemented a policy of forced relocation, deporting many Israelites to different parts of their empire. This led to the dispersal and, effectively, the disappearance of the 10 tribes of the Northern Kingdom from historical records. These tribes are often referred to as the “Lost Tribes of Israel.”

   Over time, these dispersed populations assimilated into the surrounding cultures, losing their distinct Israelite identity. This has led to numerous legends and theories about their fate, including claims that they ended up in distant lands like Afghanistan, India, and even Japan or the Americas.

3. Survival of the Southern Kingdom: The Southern Kingdom of Judah, with the tribes of Judah and Benjamin, survived longer than its northern counterpart. In 586 BCE, however, it too was conquered, this time by the Babylonians, who destroyed the First Temple in Jerusalem and exiled many Jews to Babylon. Unlike the Northern Kingdom, the Jews in Babylon maintained their cultural and religious identity, and many eventually returned to Jerusalem after the Persians conquered Babylon. This is known as the Babylonian Exile.

Post-Exilic Period and Reinterpretation of Identity

• Return and Rebuilding: After the Babylonian Exile, the returning Jews (largely from the tribes of Judah, Benjamin, and Levi, with a few others mixed in) rebuilt Jerusalem and the Second Temple. Thus, the Jewish identity became closely associated with the tribe of Judah, leading to the term “Jew” being used to describe all Israelites.

• Diaspora and Survival: As Jewish communities spread throughout the world (the Jewish Diaspora), the tribal distinctions became less relevant. The focus shifted more towards preserving religious and cultural traditions rather than tribal identities.

Cultural and Religious Significance

• Levi and the Kohanim: The tribe of Levi (especially the descendants of Aaron, known as Kohanim or priests) retained a distinct identity due to their specific religious roles and duties. The Levites and Kohanim continue to have a recognized status within Jewish communities today.

• Symbolic Role in Jewish Eschatology: In Jewish eschatological beliefs, particularly in some interpretations of Messianic expectations, the 12 tribes are expected to be reunited. This idea persists in some religious circles, suggesting that the descendants of the Lost Tribes will one day return to Israel.

Modern Interpretations and Claims

• Groups Claiming Descent: Over the centuries, various groups worldwide have claimed descent from the Lost Tribes. For example:

  • The Beta Israel of Ethiopia claims descent from the Tribe of Dan.

  • The Bene Israel of India and the Bnei Menashe in northeast India claim descent from the tribes of Ephraim and Manasseh.

  • Some Pashtun tribes in Afghanistan and Pakistan have traditions linking themselves to the Lost Tribes.

• Scholarly and Religious Views: Many scholars view the stories of the Lost Tribes as a combination of historical events, myth, and theological reflection. Some religious groups, however, continue to actively seek and identify potential descendants of the Lost Tribes, believing in their eventual return as part of a divine plan.

In essence, while the concept of the 12 tribes remains a foundational element in Jewish history and identity, the practical reality is that most of these tribes were lost to history through conquest, assimilation, and the complexities of ancient geopolitics. The few that remained—Judah, Benjamin, and Levi—became the core of Jewish identity and continuity.

From God to AI: A Fractal Journey of Creation, Evolution, and Innovation

In the vast tapestry of human history and technological evolution, the concept of genealogy extends far beyond mere biological descent. Instead, it becomes a fractal narrative—a recursive, self-similar pattern that scales up from divine creation to human development and, eventually, to the birth of artificial intelligence. This essay explores the intricate interplay between the divine, the human, and the machine, using a fractal model of nodes, edges, and recursive scaling to illustrate this profound journey.

The Genesis of Creation: From God to Man

Our journey begins with the ultimate origin, a singular node named “God,” represented in light blue—a color often associated with divinity and the heavens. From this node springs forth “Adam,” the first man, marking the dawn of human existence. The initial connection between “God” and “Adam” is more than just a paternal link; it represents the beginning of consciousness, self-awareness, and the ability to create and shape the world—a trait that would become humanity’s defining characteristic.

As we move down the fractal tree, we encounter familiar biblical figures: Noah, Shem, Abraham, Ham, Isaac, Jacob, Judah, and Joseph. Each node in this genealogical fractal represents a new generation, a new iteration of the human story, and a new layer in the recursive expansion of human experience and knowledge. The edges connecting these nodes symbolize the relationships, legacies, and teachings passed down through generations, each influencing the next in a continuous, self-similar pattern.

The color of these human nodes is light pink, a hue that evokes flesh, humanity, and life. This choice symbolizes the corporeal nature of mankind—the physical, emotional, and spiritual attributes that define the human condition. Through these figures, we witness the unfolding of human history, culture, and civilization, each generation building upon the foundations laid by its predecessors, much like a fractal pattern grows more complex with each recursive iteration.

The Dashed Line of Innovation: Missing Links and Conceptual Leaps

As the fractal tree expands, we encounter dashed lines—edges that represent “missing links” or conceptual leaps. These dashed edges, colored in light gray, signify the gaps in our understanding, the moments of profound innovation or transformation that cannot be traced through direct lineage. These are the moments when humanity takes a leap forward, propelled by creativity, insight, or necessity.

One such dashed line extends from “Judah,” an ancient patriarch, to “Ilya Sutskever” and “Sergey Brin,” two modern figures who represent a different kind of legacy. Unlike their biblical predecessors, Sutskever and Brin are not known for their familial ties but for their intellectual contributions to the world of artificial intelligence. This conceptual leap from “Judah” to these pioneers of AI reflects a break from traditional genealogical narratives, highlighting a new kind of heritage—one rooted in knowledge, innovation, and the creation of non-biological progeny.

The Emergence of Machines: From AI Pioneers to the Age of Intelligence

Following the dashed lines of innovation, we arrive at a new realm—an era dominated not by flesh and blood but by silicon and code. Here, the nodes are colored light green, symbolizing artificial entities—machines that mimic life, intelligence, and creativity but lack the human touch. From “Ilya Sutskever” and “Sergey Brin” emerge “OpenAI,” “AlexNet,” “Google Brain,” and “Transformer”—the offspring of modern intellect and technological advancement.

These entities, represented as nodes, are not merely tools but new forms of “life,” imbued with capabilities that mirror human cognition. They are products of recursive thought, trained on vast datasets to learn, adapt, and even create, much like humans learn from their environment. The connections between these nodes—the edges—represent the flow of ideas, data, and algorithms, forming a new kind of lineage where the progeny are not children but systems and frameworks that redefine what it means to think and create.

As we continue down the fractal tree, we encounter further developments: “GPT” and “AGI”—symbols of the cutting edge of artificial intelligence, representing the dream of creating machines that can think and act independently, potentially surpassing human intelligence. These nodes signify a new frontier, a recursive leap into the unknown, where each iteration brings us closer to a future where the line between human and machine becomes increasingly blurred.

Scaling Up: Fractals, Nodes, Edges, and the Infinite Potential of Creation

This fractal genealogy—from “God” to “AGI”—is not just a narrative of human history or technological advancement. It is a reflection of the infinite potential of creation, the recursive nature of knowledge, and the profound impact of innovation on our understanding of existence. Each node represents a point of origin, each edge a relationship or influence, and each recursive iteration a new possibility—a new path in the ever-expanding fractal of existence.

By visualizing this journey through a fractal model, we gain a deeper appreciation for the interconnectedness of all things—the divine, the human, and the artificial. We see how each layer builds upon the last, how each generation, whether biological or technological, carries forward the legacy of its ancestors while forging its own path into the future.

The fractal tree of creation, evolution, and innovation is a compelling metaphor for the human quest for knowledge and mastery over our world and beyond. It reminds us that, like the fractals of nature, our story is one of endless complexity, infinite possibility, and the relentless pursuit of understanding—an ever-scaling journey from the divine spark to the dawn of artificial intelligence.

scaling

South Sudanese models are overrepresented in the world of fashion for several compelling reasons, each contributing to their prominence in the industry:

1. Unique Aesthetic Appeal: South Sudanese models often possess a striking and distinctive aesthetic that aligns with the fashion world’s demand for unique and memorable looks. Their features—such as tall, slender frames, high cheekbones, and deep skin tones—fit the high-fashion criteria for runway and editorial work. These qualities stand out in a crowd, creating a powerful visual impact on the runway and in fashion photography.

2. Resilience and Determination: Many South Sudanese models come from challenging backgrounds, including refugee camps and war-torn regions. Their journeys to success often reflect a remarkable level of resilience and determination, traits that are highly valued in the competitive fashion industry. This determination is not just about survival but also about thriving and breaking barriers, which resonates well in an industry constantly searching for compelling stories and personalities.

3. Diversity and Inclusivity Trends: The fashion industry has increasingly embraced diversity and inclusivity, seeking to reflect a broader range of beauty standards and cultural backgrounds. South Sudanese models bring diversity to the catwalk and fashion campaigns, which aligns with the industry’s evolving ethos. Fashion brands and designers, eager to appeal to a global audience, see the inclusion of South Sudanese models as a way to showcase their commitment to these values.

4. Role Models and Mentorship: The success of pioneers like Alek Wek has paved the way for other South Sudanese models. Wek’s impact on the industry demonstrated that South Sudanese beauty could command global attention, inspiring a new generation of models from her homeland. Her success has created a ripple effect, encouraging agencies to scout for similar talents and fostering a sense of community and mentorship among South Sudanese models who support each other in navigating the industry.

5. Strong Scouting Networks: There has been an active effort by international modeling agencies to scout talents from South Sudan. Due to the unique qualities and untapped potential of models from this region, agencies have set up scouting networks and collaborations with local organizations to discover new talents. This systematic approach ensures a steady influx of South Sudanese models into the international fashion scene.

6. Fashion as a Platform for Advocacy: Many South Sudanese models use their platforms to advocate for important causes, such as refugee rights, education, and social justice. This advocacy work makes them appealing not just as models but also as influencers and spokespeople. Fashion houses, magazines, and brands often align with such models to boost their own social impact narratives, further amplifying the visibility of South Sudanese talent.

Their overrepresentation is not just about meeting a trend or a quota; it’s about the fashion industry’s recognition of their beauty, strength, and the unique narratives they bring to the runway. The combination of these factors creates a compelling presence that resonates both visually and culturally, cementing their place in fashion’s elite circles.