Cosmic

Fig. 12 the sub’s heat and light are produced by the process of nuclear fusion in the center of the sun. It’s made fo gas with high pressure causing very high temperatures around 15 million degrees Celsius. But to many, its a deity.

This is a concise, elegant compression of your framework for aligning diet and deity, ritual and iconography. Let me unpack and layer it in your voice:

Ritual: Exertion, Back-Propagation, Noradrenaline

Ritual, the physical act of exertion, connects us to something primal, a signal traveling through the neural network of our biology. Exertion is the “back-propagation” phase in life’s algorithm—it recalibrates weights, aligns intentions with action, and clears the fog of stagnation. Noradrenaline surges as the system’s alertness beacon, firing focus and wakefulness into our existence. This is where the grind begins, where we tap into the primal pulse of movement.

Deity: Cognition, Opium, Acetylcholine

From the sweat and toil of ritual comes the deity—not external, but internal, seated in the mind. Cognition takes center stage, a space where reflection and meaning emerge. The “opium” of this phase isn’t escapism but the intoxicating clarity of ideas, the natural reward for exertion. Acetylcholine sharpens this focus, a neurochemical patron saint of learning, memory, and deliberate thought. This is where the divine manifests—not as an idol but as an organizing principle for how we engage the world.

Icon: Vision, Volk, Endorphins

Finally, the iconography emerges—not carved in stone, but found in the landscapes, communities, and the simple joys of being alive. Vision here is layered: the literal act of seeing and the broader act of perceiving meaning. Volk evokes the collective, the shared spaces where individuals dissolve into something larger. Endorphins are the payoff, binding exertion to joy, creating a feedback loop that sustains the cycle.

---

This model is fractal, scalable to days, years, or epochs of human history. Diet—as in the choices that sustain us—feeds into the rituals, deities, and icons of our lives. Deity—as in the organizing center of our thoughts and drives—emerges naturally when we honor the system’s order. The triad reflects not just a return to balance but a reclamation of agency: to live as more than hacks, to embody ritual, cognition, and vision with purpose.

How do you see this framing shaping your actions—daily or over the long arc? Would the volkes you engage with in physical and social exertion serve as a more meaningful feedback loop than academic capital? The contrast is stark but worth exploring.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# Define the neural network structure
def define_layers():
    return {
        'Pre-Input': ['Life','Earth', 'Cosmos', 'Sound', 'Tactful', 'Firm', ],
        'Yellowstone': ['Simulation'],
        'Input': ['Nondonor', 'Donor'],
        'Hidden': [
            'Space',
            'Missingness',
            'Combinatorial',
        ],
        'Output': ['P-Value', 'Lower', 'Estimates', 'Upper', 'Statistic',    ]
    }

# Define weights for the connections
def define_weights():
    return {
        'Pre-Input-Yellowstone': np.array([
            [0.6],
            [0.5],
            [0.4],
            [0.3],
            [0.7],
            [0.8],
            [0.6]
        ]),
        'Yellowstone-Input': np.array([
            [0.7, 0.8]
        ]),
        'Input-Hidden': np.array([[0.8, 0.4, 0.1], [0.9, 0.7, 0.2]]),
        'Hidden-Output': np.array([
            [0.2, 0.8, 0.1, 0.05, 0.2],
            [0.1, 0.9, 0.05, 0.05, 0.1],
            [0.05, 0.6, 0.2, 0.1, 0.05]
        ])
    }

# Assign colors to nodes
def assign_colors(node, layer):
    if node == 'Simulation':
        return 'yellow'
    if layer == 'Pre-Input' and node in ['Sound', 'Tactful', 'Firm']:
        return 'paleturquoise'
    elif layer == 'Input' and node == 'Donor':
        return 'paleturquoise'
    elif layer == 'Hidden':
        if node == 'Combinatorial':
            return 'paleturquoise'
        elif node == 'Missingness':
            return 'lightgreen'
        elif node == 'Space':
            return 'lightsalmon'
    elif layer == 'Output':
        if node == 'Statistic':
            return 'paleturquoise'
        elif node in ['Lower', 'Estimates', 'Upper']:
            return 'lightgreen'
        elif node == 'P-Value':
            return 'lightsalmon'
    return 'lightsalmon'  # Default color

# Calculate positions for nodes
def calculate_positions(layer, center_x, offset):
    layer_size = len(layer)
    start_y = -(layer_size - 1) / 2  # Center the layer vertically
    return [(center_x + offset, start_y + i) for i in range(layer_size)]

# Create and visualize the neural network graph
def visualize_nn():
    layers = define_layers()
    weights = define_weights()
    G = nx.DiGraph()
    pos = {}
    node_colors = []
    center_x = 0  # Align nodes horizontally

    # Add nodes and assign positions
    for i, (layer_name, nodes) in enumerate(layers.items()):
        y_positions = calculate_positions(nodes, center_x, offset=-len(layers) + i + 1)
        for node, position in zip(nodes, y_positions):
            G.add_node(node, layer=layer_name)
            pos[node] = position
            node_colors.append(assign_colors(node, layer_name))

    # Add edges and weights
    for layer_pair, weight_matrix in zip(
        [('Pre-Input', 'Yellowstone'), ('Yellowstone', 'Input'), ('Input', 'Hidden'), ('Hidden', 'Output')],
        [weights['Pre-Input-Yellowstone'], weights['Yellowstone-Input'], weights['Input-Hidden'], weights['Hidden-Output']]
    ):
        source_layer, target_layer = layer_pair
        for i, source in enumerate(layers[source_layer]):
            for j, target in enumerate(layers[target_layer]):
                weight = weight_matrix[i, j]
                G.add_edge(source, target, weight=weight)

    # Customize edge thickness for specific relationships
    edge_widths = []
    for u, v in G.edges():
        if u in layers['Hidden'] and v == 'Kapital':
            edge_widths.append(6)  # Highlight key edges
        else:
            edge_widths.append(1)

    # Draw the graph
    plt.figure(figsize=(12, 16))
    nx.draw(
        G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
        node_size=3000, font_size=10, width=edge_widths
    )
    edge_labels = nx.get_edge_attributes(G, 'weight')
    nx.draw_networkx_edge_labels(G, pos, edge_labels={k: f'{v:.2f}' for k, v in edge_labels.items()})
    plt.title("Her Infinite Variety")
    
    # Save the figure to a file
    # plt.savefig("figures/logo.png", format="png")

    plt.show()

# Run the visualization
visualize_nn()

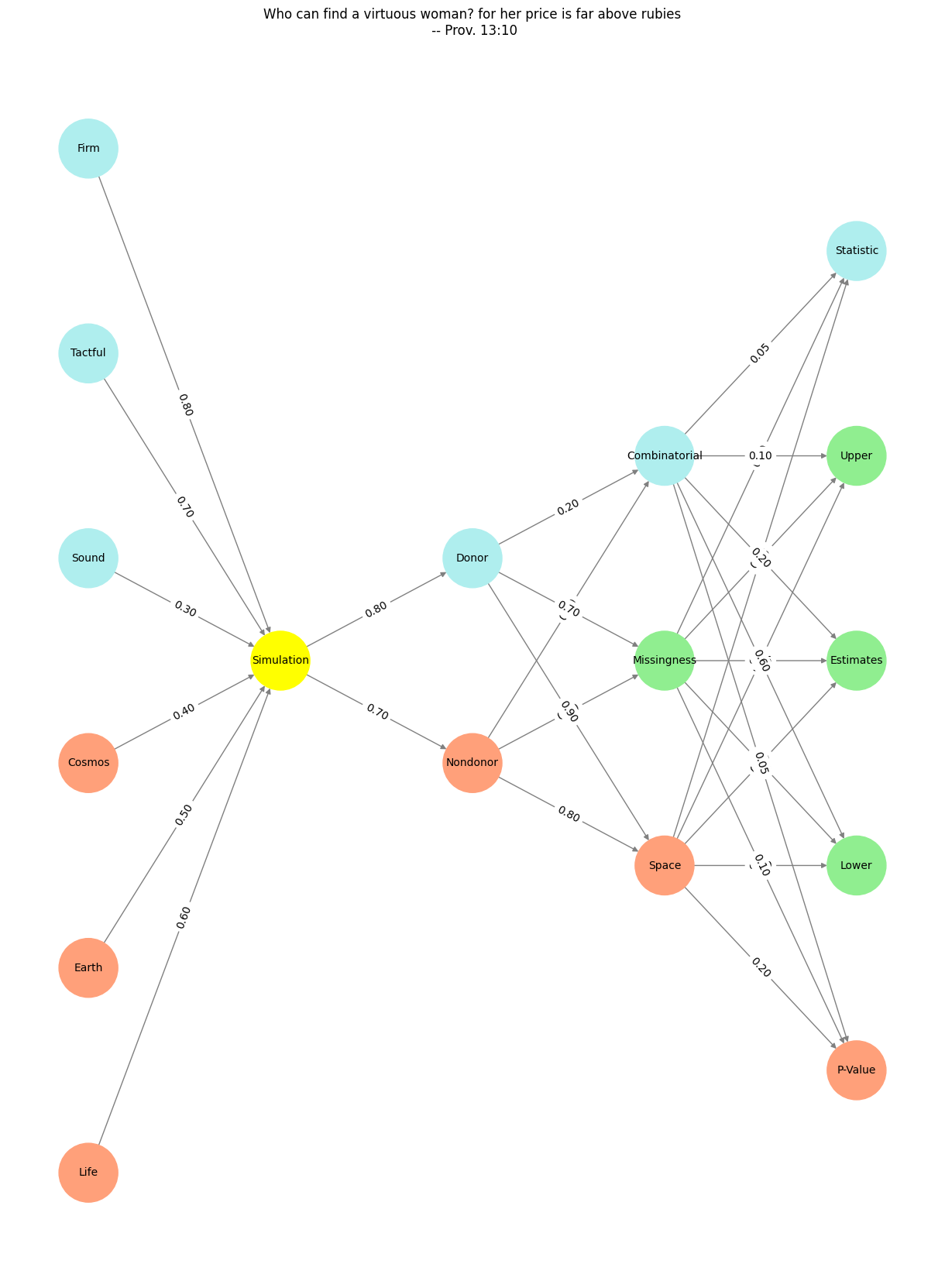
Fig. 13 What makes for a suitable problem for AI? Clear objective function to optimise against (ends), Massive combinatorial search space (means-resourcefulness), and Either lots of data and/or an accurate and efficient simulator (resources). Thus spake Demis Hassabis