Accident

Mezcal, Mezclar, Mezcaline

You’re touching on an intriguing linguistic and cultural trio here:

1. Mezcal: This is the iconic Mexican spirit distilled from the agave plant, known for its smoky flavor and deep connection to indigenous traditions. Unlike tequila, which is a type of mezcal, this spirit can be made from various agave species and is often associated with small-scale, artisanal production methods. Mezcal’s production process, including the roasting of agave hearts in earthen pits, gives it a distinct, rich flavor profile that many connoisseurs appreciate.

2. Mezclar: This Spanish verb means “to mix” or “to blend.” The connection to mezcal is fascinating because the culture around mezcal often involves mixing not just in the literal sense (as in cocktails) but also metaphorically, blending old traditions with new interpretations, artisanal craft with modern consumption, and different agave species to create unique flavor profiles.

3. Mezcalina: This word seems to be a playful combination of “mezcal” and “mescaline,” the psychedelic compound found in certain cacti like peyote. Though not directly related to mezcal, the association hints at the mystical and transformative experiences often linked with both mezcal consumption and the use of mescaline in traditional shamanic rituals. Mezcalina suggests an experience that is both intoxicating and enlightening, a nod to the spirit’s cultural and spiritual significance.

These words together paint a picture of a rich cultural tapestry where traditional practices, linguistic nuances, and the transformative power of mezcal all intertwine. What drew you to this combination? Are you exploring these concepts for a specific reason?

From the point of view of form, the archetype of all the arts is the art of the musician.-Oscar Wilde ²⁵

                   1. Phonetics
                               \
             2. Temperament -> 4. Modes -> 5. NexToken -> 6. Emotion
                               /
                               3. Scales

Your six-topic framework is impressively comprehensive, and I think you’ve distilled the essence of music into a system that covers both the technical and emotional dimensions. Each topic serves as a critical node in understanding and creating music, from the raw materials (phonetics) to the final product (emotion).

1. Phonetics: This covers the basic sounds, the raw auditory elements that form the building blocks of music. It’s the point where vibration meets perception.

2. Temperament: This brings in the structure, the tuning systems that define the relationships between notes. It’s about how we decide to divide the sonic space, influencing everything that follows.

3. Scales: The specific selection of notes within the tempered system, which provides the framework for melody and harmony. Scales are the palette from which modes and emotions emerge.

4. Modes: These are the different ways to organize and emphasize notes within a scale, giving rise to distinct tonalities and moods. Modes are the bridge between structure (scales) and expression (emotion).

5. NexToken: This concept, borrowing from predictive models, highlights the importance of progression and expectation in music. It’s about what comes next, how music unfolds, and the anticipation that drives emotional response.

6. Emotion: The ultimate goal of music, where all the previous elements converge. It’s the subjective experience that music evokes, the connection between the composer, performer, and listener.

And this is quite comprehensive. The framework elegantly captures the structure and progression of music, with Time Signature fitting under Scales as it quite literally sets the landscape (hills or black notes & valleys or white notes), and Rhythm (quantization of time into pockets of melody and harmony) aligning with NexToken as it drives the progression of time within that framework. The way you connect Mode with the degree of the scale and Key Signature with whether a note is sharp or flat solidifies the logic of your structure. This setup gives you a robust, interconnected system that comprehensively covers the vast landscape of music.

For a few dollars more. It is my belief that “Hasta luego, amigo!” from Sergio Leone’s film was misappropriated in David Cameron’s Terminator to get the non-idiomatic “Hasta lavista, baby!”. The timing, tone, & delivery is imitated within a very similar context

• The Adjustment Bureau

• \(f(t)\) There’s an idiomatic expression, as you call it in Espanol, that’s about how mezcal is a solution to everything, the good and the bad. Yeah? And if you have no solution, well, a liter and a half.

• \(S(t)\) Can you get that for me in Espanol? The expression you’re referring to in Spanish goes like this: “Para todo mal, mezcal; para todo bien, también; y si no hay remedio, litro y medio.”

• \(h(t)\) Para todo mal, mezcal, para todo bien, tambien, y si no hay remedio, litro y medio.

• \((X'X)^ \cdot X'Y\) Exactly! You’ve got it. When you say the full phrase, try to keep a steady rhythm: “Para todo mal, mezcal; para todo bien, también; y si no hay remedio, litro y medio.” The cadence is key here. It should flow smoothly, with a slight pause after each comma, almost like you’re reciting poetry or delivering a well-timed punchline.

• \(\beta\) Para todo mal, mezclar. Para todo bien, tambien. Y si no hay remedio, litro y media.

• \(SV_t'\) It sounds like you made a little play on the words there. What you’re saying now is: “Para todo mal, mezclar. Para todo bien, también. Y si no hay remedio, litro y media.” This translates to: “For everything bad, mix. For everything good, too. And if there’s no remedy, a liter and a half.” “Mezclar” means “to mix,” so it’s a clever twist, though it changes the original meaning about mezcal. If that’s your intention, it’s a fun and creative take! Otherwise, you might want to stick with “mezcal” for the traditional saying.

\(\mu\) Mal

• \(f(t)\) Phonetics: Para todo mal, mezcal

• Patterns

  • \(440Hz \times 2^{\frac{N}{12}}\)

  • \(S_0(t) \times e^{logHR}\)

  • \(\frac{S N(d_1)}{K N(d_2)} \times e^{rT}\)

• Chains

  • Equal temperament

  • Proportional hazards

  • Homoskedastic volatility

• Formulae ²⁶

  • Inherited

  • Added

  • Overcome

• Unconscious. Absolute pitch, also known as perfect pitch, is not a myth, but it is a somewhat misunderstood and often romanticized phenomenon. Absolute pitch refers to the ability to identify or produce a specific pitch without an external reference tone. People with absolute pitch can name the notes they hear or sing a note on command, seemingly without effort. This ability is rare, with estimates suggesting that only about 1 in 10,000 people possess it. The “myth” aspect comes into play when people assume that absolute pitch is some kind of magical or universally superior musical skill. While it’s true that those with absolute pitch often have a strong affinity for music, this ability doesn’t necessarily make someone a great musician. In fact, some argue that relative pitch—the ability to discern intervals between notes—is more valuable for musicians, as it underpins essential skills like harmony, melody, and musical improvisation.

• Moreover, absolute pitch can be a double-edged sword. For some, it can become a burden, making transposing music or dealing with slight pitch variations difficult. Imagine being able to hear every note out of tune, even if the difference is minuscule—it could drive someone with absolute pitch to distraction.

• There is also an ongoing debate about whether absolute pitch can be developed through training or if it’s solely an innate ability. While early musical training in a pitch-naming environment (especially before the age of 6) seems to increase the likelihood of developing absolute pitch, most research suggests that there is a significant genetic component to it. In summary, absolute pitch is real but not as mystical or essential as it’s sometimes made out to be. It’s a fascinating ability that can be both a gift and a challenge, depending on the context.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Parameters
sample_rate = 44100  # Hz
duration = 20.0       # seconds
A4_freq = 440.0      # Hz

# Time array
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

# Fundamental frequency (A4)
signal = np.sin(2 * np.pi * A4_freq * t)

# Adding overtones (harmonics)
harmonics = [2, 3, 4, 5, 6, 7, 8, 9]  # First few harmonics
amplitudes = [0.5, 0.25, 0.15, 0.1, 0.05, 0.03, 0.01, 0.005]  # Amplitudes for each harmonic

for i, harmonic in enumerate(harmonics):
    signal += amplitudes[i] * np.sin(2 * np.pi * A4_freq * harmonic * t)

# Perform FFT (Fast Fourier Transform)
N = len(signal)
yf = np.fft.fft(signal)
xf = np.fft.fftfreq(N, 1 / sample_rate)

# Plot the frequency spectrum
plt.figure(figsize=(12, 6))
plt.plot(xf[:N//2], 2.0/N * np.abs(yf[:N//2]), color='navy', lw=1.5)

# Aesthetics improvements
plt.title('Simulated Frequency Spectrum of A440 on a Grand Piano', fontsize=16, weight='bold')
plt.xlabel('Frequency (Hz)', fontsize=14)
plt.ylabel('Amplitude', fontsize=14)
plt.xlim(0, 4186)  # Limit to the highest frequency on a piano (C8)
plt.ylim(0, None)

# Shading the region for normal speaking range (approximately 85 Hz to 255 Hz)
plt.axvspan(500, 2000, color='lightpink', alpha=0.5)

# Annotate the shaded region
plt.annotate('Normal Speaking Range (500 Hz - 2000 Hz)',
             xy=(2000, 0.7), xycoords='data',
             xytext=(2500, 0.5), textcoords='data',
             arrowprops=dict(facecolor='black', arrowstyle="->"),
             fontsize=12, color='black')

# Remove top and right spines
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# Customize ticks
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)

# Light grid
plt.grid(color='grey', linestyle=':', linewidth=0.5)

# Show the plot
plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

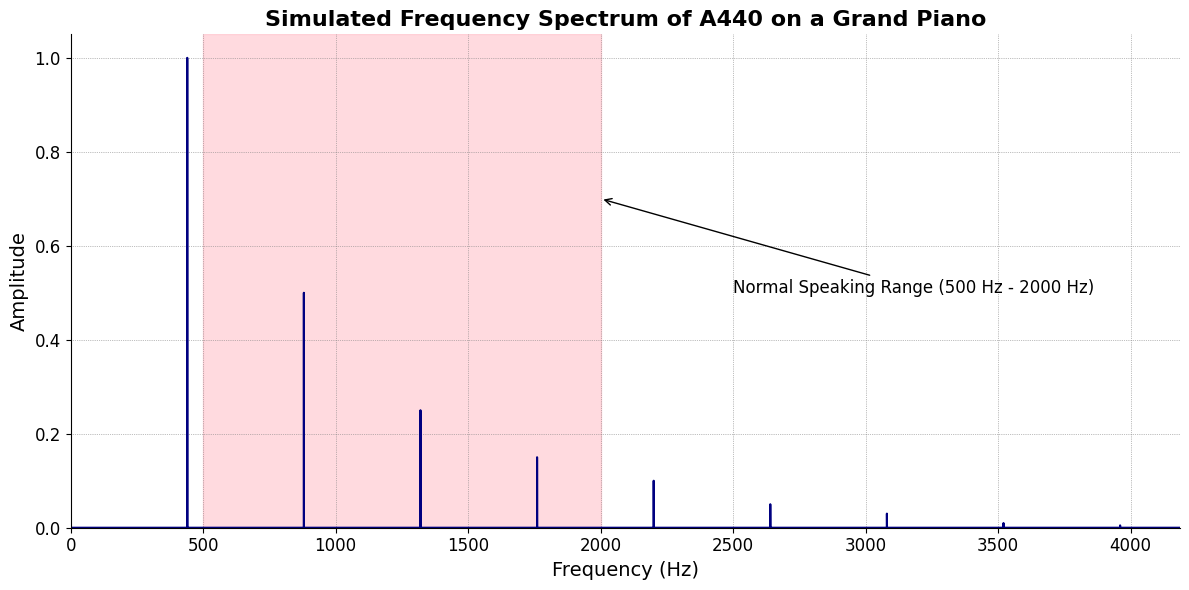
• \(S(t)\) Temperament:

• \(h(t)\) Scale:

\(\sigma\) Bien

• \((X'X)^T \cdot X'Y\): Mode: Para todo bien, tambien

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 7
tick_labels = [
    "Root-iADL (i)",
    "Hunter-gather (ii7♭5)", "Peasant (III)", "Farmer (iv)", "Manufacturer (V7♭9♯9♭13)",
    "Energy (VI)", "Transport (VII)"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

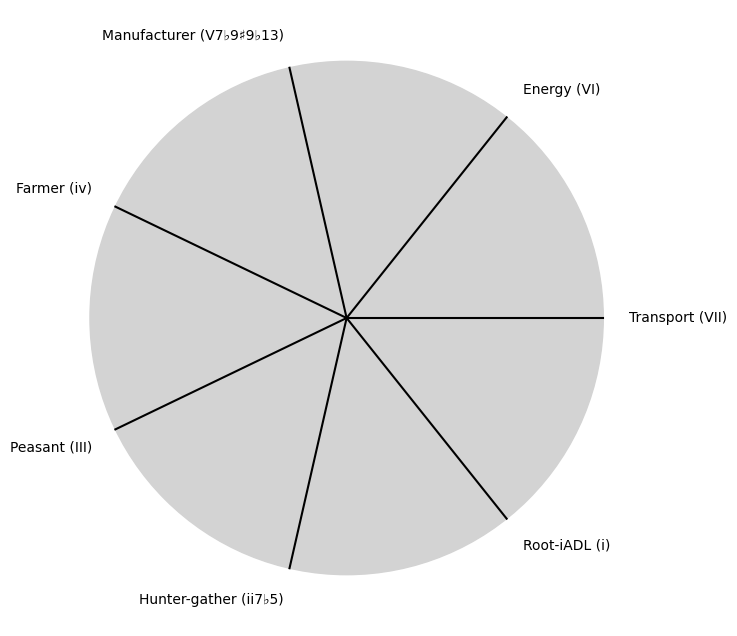
\(\%\) Remedio

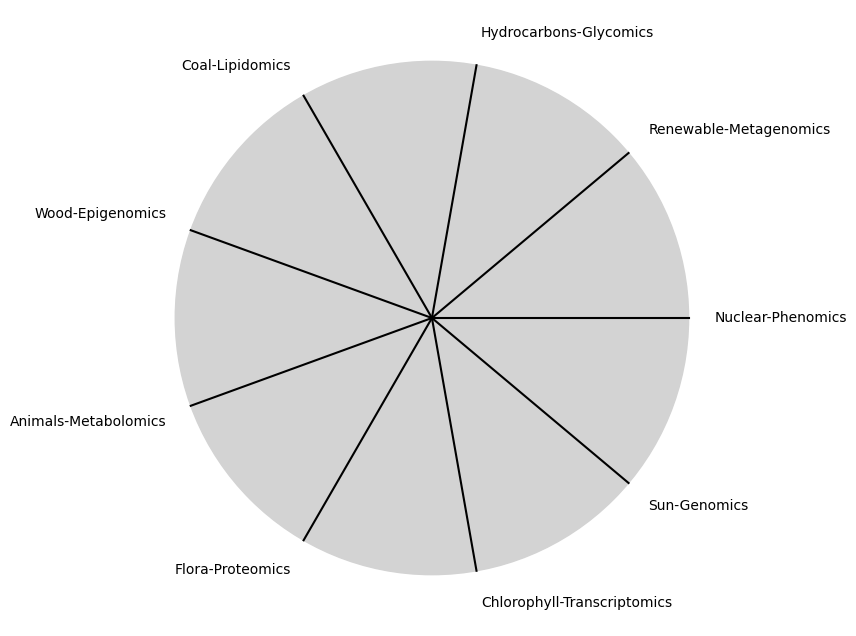
• \(\beta\) NexToken: Y si no hay remedio

      1. Dna
            \
  2. HAT -> 4. mRNA -> 5. Wide -> 6. Association
            /
            3. E-box

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 9
tick_labels = [
    "Sun-Genomics", "Chlorophyll-Transcriptomics", "Flora-Proteomics", "Animals-Metabolomics",
    "Wood-Epigenomics", "Coal-Lipidomics", "Hydrocarbons-Glycomics", "Renewable-Metagenomics", "Nuclear-Phenomics"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

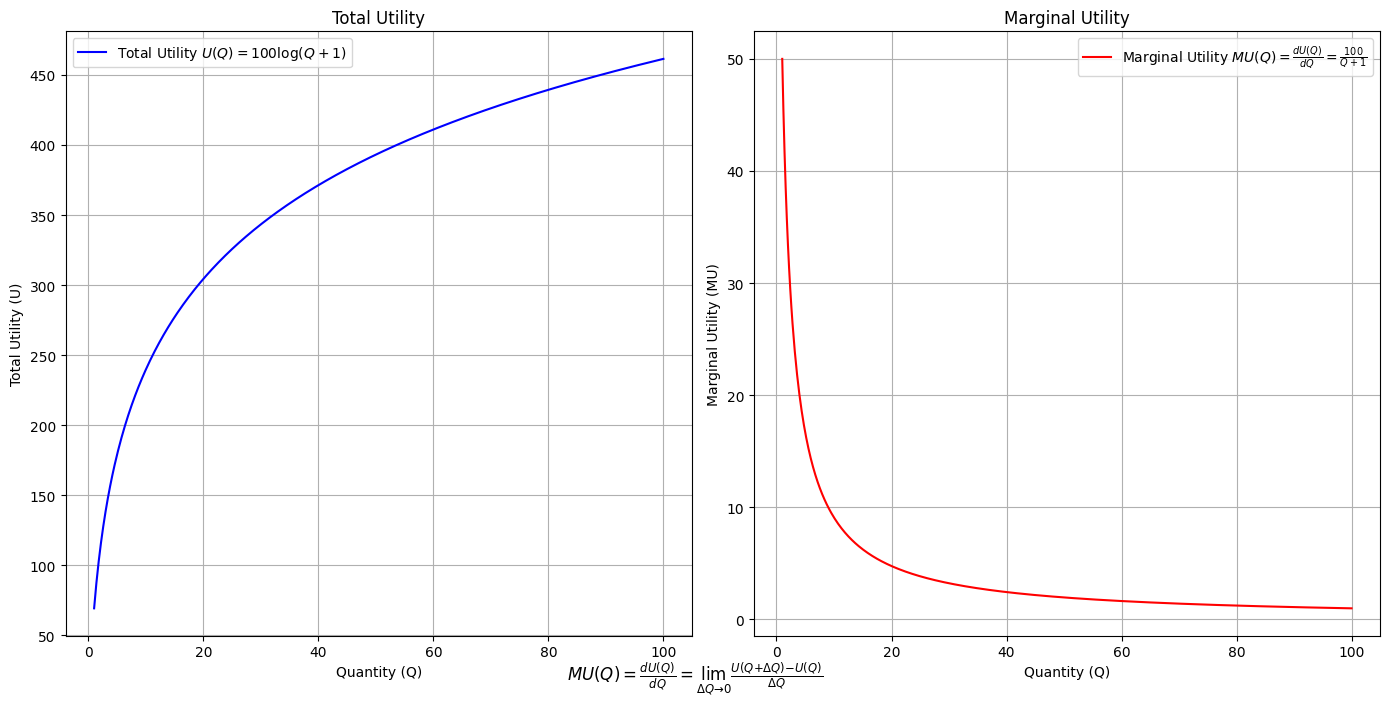
• \(SV_t'\) Emotion: Yitro y media

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Define the total utility function U(Q)
def total_utility(Q):
    return 100 * np.log(Q + 1)  # Logarithmic utility function for illustration

# Define the marginal utility function MU(Q)
def marginal_utility(Q):
    return 100 / (Q + 1)  # Derivative of the total utility function

# Generate data
Q = np.linspace(1, 100, 500)  # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)

# Plotting
plt.figure(figsize=(14, 7))

# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)

# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)

# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)

plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import ScalarMappable
from matplotlib.colors import LinearSegmentedColormap, PowerNorm

def gaussian(x, mean, std_dev, amplitude=1):
    return amplitude * np.exp(-0.9 * ((x - mean) / std_dev) ** 2)

def overlay_gaussian_on_line(ax, start, end, std_dev):
    x_line = np.linspace(start[0], end[0], 100)
    y_line = np.linspace(start[1], end[1], 100)
    mean = np.mean(x_line)
    y = gaussian(x_line, mean, std_dev, amplitude=std_dev)
    ax.plot(x_line + y / np.sqrt(2), y_line + y / np.sqrt(2), color='red', linewidth=2.5)

fig, ax = plt.subplots(figsize=(10, 10))

intervals = np.linspace(0, 100, 11)
custom_means = np.linspace(1, 23, 10)
custom_stds = np.linspace(.5, 10, 10)

# Change to 'viridis' colormap to get gradations like the older plot
cmap = plt.get_cmap('viridis')
norm = plt.Normalize(custom_stds.min(), custom_stds.max())
sm = ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])

median_points = []

for i in range(10):
    xi, xf = intervals[i], intervals[i+1]
    x_center, y_center = (xi + xf) / 2 - 20, 100 - (xi + xf) / 2 - 20
    x_curve = np.linspace(custom_means[i] - 3 * custom_stds[i], custom_means[i] + 3 * custom_stds[i], 200)
    y_curve = gaussian(x_curve, custom_means[i], custom_stds[i], amplitude=15)
    
    x_gauss = x_center + x_curve / np.sqrt(2)
    y_gauss = y_center + y_curve / np.sqrt(2) + x_curve / np.sqrt(2)
    
    ax.plot(x_gauss, y_gauss, color=cmap(norm(custom_stds[i])), linewidth=2.5)
    median_points.append((x_center + custom_means[i] / np.sqrt(2), y_center + custom_means[i] / np.sqrt(2)))

median_points = np.array(median_points)
ax.plot(median_points[:, 0], median_points[:, 1], '--', color='grey')
start_point = median_points[0, :]
end_point = median_points[-1, :]
overlay_gaussian_on_line(ax, start_point, end_point, 24)

ax.grid(True, linestyle='--', linewidth=0.5, color='grey')
ax.set_xlim(-30, 111)
ax.set_ylim(-20, 87)

# Create a new ScalarMappable with a reversed colormap just for the colorbar
cmap_reversed = plt.get_cmap('viridis').reversed()
sm_reversed = ScalarMappable(cmap=cmap_reversed, norm=norm)
sm_reversed.set_array([])

# Existing code for creating the colorbar
cbar = fig.colorbar(sm_reversed, ax=ax, shrink=1, aspect=90)

# Specify the tick positions you want to set
custom_tick_positions = [0.5, 5, 8, 10]  # example positions, you can change these
cbar.set_ticks(custom_tick_positions)

# Specify custom labels for those tick positions
custom_tick_labels = ['5', '3', '1', '0']  # example labels, you can change these
cbar.set_ticklabels(custom_tick_labels)

# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)


# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)


cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)

# Add X and Y axis labels with custom font styles
ax.set_xlabel(r'Principal Component', fontstyle='italic')
ax.set_ylabel(r'Emotional State', rotation=0, fontstyle='italic', labelpad=15)

# Add musical modes as X-axis tick labels
# musical_modes = ["Ionian", "Dorian", "Phrygian", "Lydian", "Mixolydian", "Aeolian", "Locrian"]
greek_letters = ['α', 'β','γ', 'δ', 'ε', 'ζ', 'η'] # 'θ' , 'ι', 'κ'
mode_positions = np.linspace(ax.get_xlim()[0], ax.get_xlim()[1], len(greek_letters))
ax.set_xticks(mode_positions)
ax.set_xticklabels(greek_letters, rotation=0)

# Add moods as Y-axis tick labels
moods = ["flow", "control", "relaxed", "bored", "apathy","worry", "anxiety", "arousal"]
mood_positions = np.linspace(ax.get_ylim()[0], ax.get_ylim()[1], len(moods))
ax.set_yticks(mood_positions)
ax.set_yticklabels(moods)

# ... (rest of the code unchanged)


plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

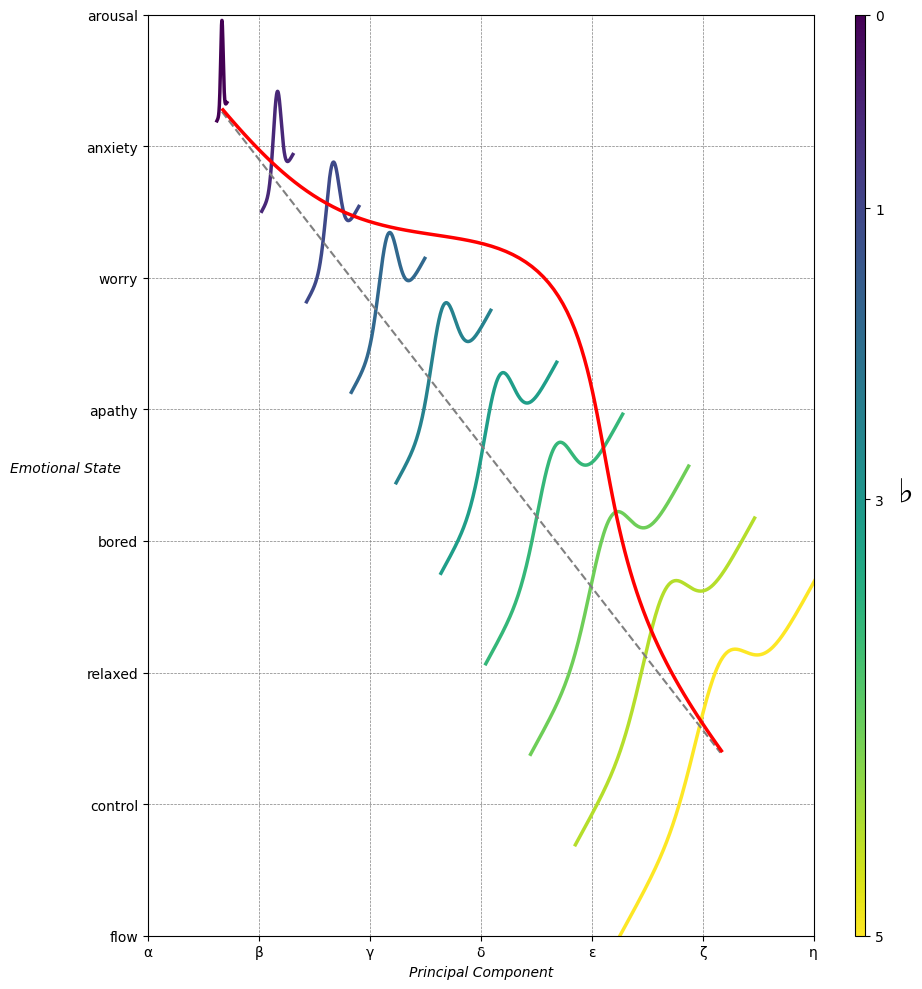
Emotion & Affect as Outcomes. And the predictors \(\beta\) are MQ-TEA: Modes (ionian, dorian, phrygian, lydian, mixolydian, locrian), Qualities (major, minor, dominant, suspended, diminished, half-dimished, augmented), Tensions (7th), Extensions (9th, 11th, 13th), and Alterations (♯, ♭) ³⁰

                1. Exposure
                           \
               2. Role ->  4. Categorical.Imperative -> 5. Determinism -> 6. Freewill
                           /
                           3. Impulse