Aging

Energy

From the point of view of form, the archetype of all the arts is the art of the musician.-Oscar Wilde ²⁷

                1. Sensory
                          \
             2. Memory -> 4. Frailty -> 5. Omics -> 6. Independence
                          /
                          3. Agility

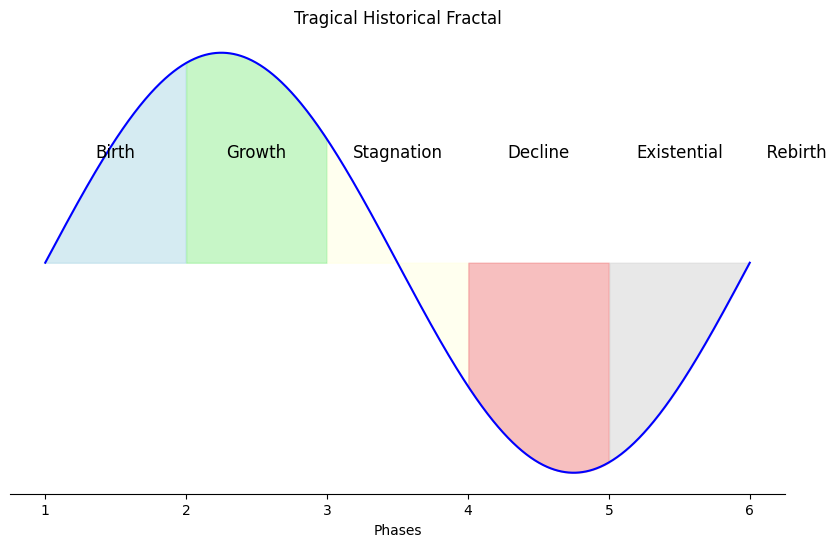
When does aging begin?. From the ii-V7-i theme of a character arc, What variations might we perceive here? What departure-struggle-return? For our protagonist it is (ii) metabolism \(f(t)\), age \(S(t)\), energy \(h(t)\), encoded as (V7) frailty \((X'X)^T \cdot X'Y\), decoded as (i) determinism \(\beta\) vs. freewill \(SV_t'\). As a part of cosmic dirt, we departed from lifeless forms & manifested that with life & the energy of youth ii. But there’s a steady loss of energy from conception to death & the entirety of life is a losing battle against our return to cosmic dust V7. It is predetermined that we all complete the arc from dust-to-dust i. Lookout for the sentinal evidence from our sensory acuity (vision, olfaction, audition, gustation, chemistry, balance), cognitive state (memory, learning, updating) and motor agility (calories/day, m/s, dynamometer, bone-density, reflex-speed, falls, gymnastic-feats, vertigo). These encode all the insults that time & comorbidity bring upon the body, into a latent-space of the physical frailty phenotype, which may be decoded using -omics, and ultimately GRIP with predictive accuracy for loss of independence in activities of daily living.

• The Adjustment Bureau

• Hearing loss as risk factor for cognitive decline

• Sound-attenuated booth for quantification

• Participant wears headset:: 500-2000 Hz (normal speech)

  • \(\lt 25 dB\) : no loss

  • \(25-40 dB\) : mild

  • \(40-60 dB\) : moderate

  • \(\geq 60 dB\) : severe

• This conflict is often portrayed in narratives where characters are forced to choose between following their heart and adhering to the norms of the group, be it a family, community, or institution. The “Adjustment Bureau” you mentioned, whether metaphorical or literal, represent the forces that attempt to maintain order by curbing individuality and ensuring conformity in line with the categorical imperative. They’re like the unseen hands of fate, working to suppress or redirect those impulses that threaten the stability of the collective unconscious \((X'X)^T \cdot X'Y\).

• In many ways, this struggle reflects the larger theme of free will \(SV_t'\) versus

• Determinism \(\beta\). Are we free to act on our emotions and impulses, or are we bound by the duties and traditions we’ve inherited? The beauty and tragedy of this conflict lie in the fact that there’s no simple resolution—it’s an eternal push and pull, where the outcome is never certain. Characters who wrestle with this dilemma are often the most compelling because they embody the human condition in its rawest form. They challenge the status quo, disrupt the carefully maintained order, and force a reckoning between personal authenticity and societal expectations. And in this clash, there’s often no clear winner, just a deeper understanding of the costs and consequences of choosing one path over the other.

\(\mu\) Base-case

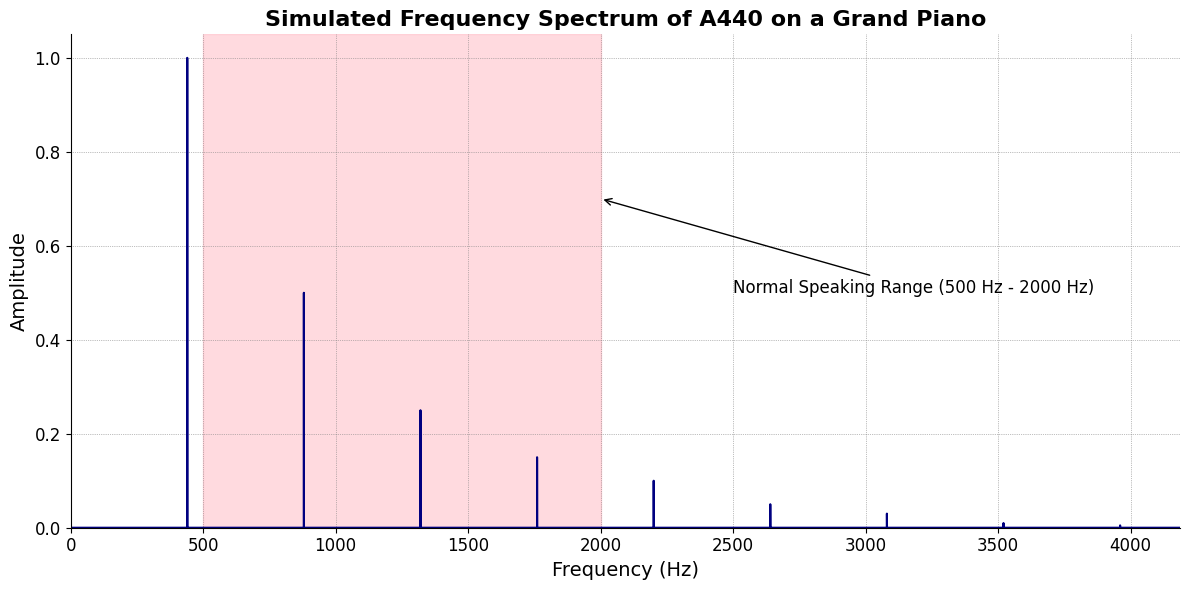
• \(f(t)\) Senses: Note that A4-A6 is normal range for human speech

• Patterns

  • \(440Hz \times 2^{\frac{N}{12}}\)

  • \(S_0(t) \times e^{logHR}\)

  • \(\frac{S N(d_1)}{K N(d_2)} \times e^{rT}\)

• Chains

  • Equal temperament

  • Proportional hazards

  • Homoskedastic volatility

• Formulae ²⁸

  • Inherited

  • Added

  • Overcome

• Unconscious. Absolute pitch, also known as perfect pitch, is not a myth, but it is a somewhat misunderstood and often romanticized phenomenon. Absolute pitch refers to the ability to identify or produce a specific pitch without an external reference tone. People with absolute pitch can name the notes they hear or sing a note on command, seemingly without effort. This ability is rare, with estimates suggesting that only about 1 in 10,000 people possess it. The “myth” aspect comes into play when people assume that absolute pitch is some kind of magical or universally superior musical skill. While it’s true that those with absolute pitch often have a strong affinity for music, this ability doesn’t necessarily make someone a great musician. In fact, some argue that relative pitch—the ability to discern intervals between notes—is more valuable for musicians, as it underpins essential skills like harmony, melody, and musical improvisation.

• Moreover, absolute pitch can be a double-edged sword. For some, it can become a burden, making transposing music or dealing with slight pitch variations difficult. Imagine being able to hear every note out of tune, even if the difference is minuscule—it could drive someone with absolute pitch to distraction.

• There is also an ongoing debate about whether absolute pitch can be developed through training or if it’s solely an innate ability. While early musical training in a pitch-naming environment (especially before the age of 6) seems to increase the likelihood of developing absolute pitch, most research suggests that there is a significant genetic component to it. In summary, absolute pitch is real but not as mystical or essential as it’s sometimes made out to be. It’s a fascinating ability that can be both a gift and a challenge, depending on the context.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Parameters
sample_rate = 44100  # Hz
duration = 20.0       # seconds
A4_freq = 440.0      # Hz

# Time array
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

# Fundamental frequency (A4)
signal = np.sin(2 * np.pi * A4_freq * t)

# Adding overtones (harmonics)
harmonics = [2, 3, 4, 5, 6, 7, 8, 9]  # First few harmonics
amplitudes = [0.5, 0.25, 0.15, 0.1, 0.05, 0.03, 0.01, 0.005]  # Amplitudes for each harmonic

for i, harmonic in enumerate(harmonics):
    signal += amplitudes[i] * np.sin(2 * np.pi * A4_freq * harmonic * t)

# Perform FFT (Fast Fourier Transform)
N = len(signal)
yf = np.fft.fft(signal)
xf = np.fft.fftfreq(N, 1 / sample_rate)

# Plot the frequency spectrum
plt.figure(figsize=(12, 6))
plt.plot(xf[:N//2], 2.0/N * np.abs(yf[:N//2]), color='navy', lw=1.5)

# Aesthetics improvements
plt.title('Simulated Frequency Spectrum of A440 on a Grand Piano', fontsize=16, weight='bold')
plt.xlabel('Frequency (Hz)', fontsize=14)
plt.ylabel('Amplitude', fontsize=14)
plt.xlim(0, 4186)  # Limit to the highest frequency on a piano (C8)
plt.ylim(0, None)

# Shading the region for normal speaking range (approximately 85 Hz to 255 Hz)
plt.axvspan(500, 2000, color='lightpink', alpha=0.5)

# Annotate the shaded region
plt.annotate('Normal Speaking Range (500 Hz - 2000 Hz)',
             xy=(2000, 0.7), xycoords='data',
             xytext=(2500, 0.5), textcoords='data',
             arrowprops=dict(facecolor='black', arrowstyle="->"),
             fontsize=12, color='black')

# Remove top and right spines
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# Customize ticks
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)

# Light grid
plt.grid(color='grey', linestyle=':', linewidth=0.5)

# Show the plot
plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

• \(S(t)\) Memory: What quick tests are out there?

• \(h(t)\) Emotions: Let’s focus on how they translate to motion!

\(\sigma\) Varcov-matrix

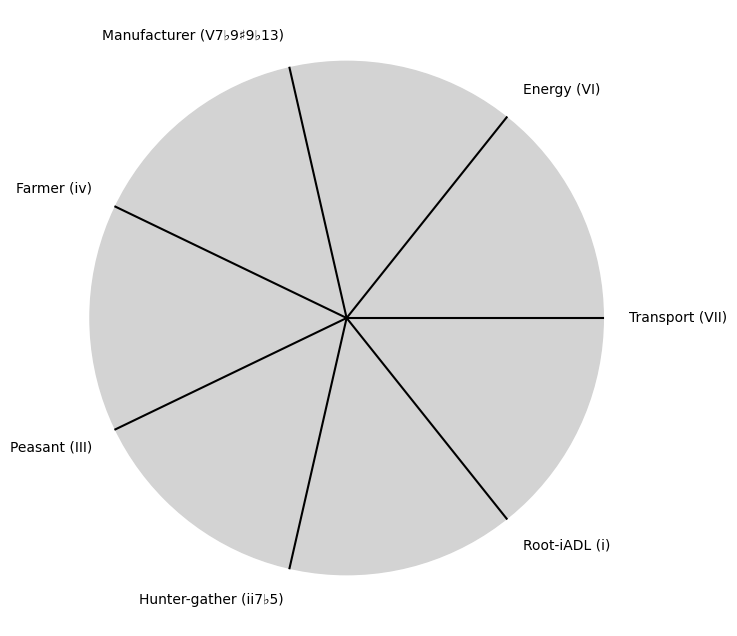
• \((X'X)^T \cdot X'Y\): Frailty: Energy, Omics, Activity, Muscle, Strength, Pace,

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 7
tick_labels = [
    "Root-iADL (i)",
    "Hunter-gather (ii7♭5)", "Peasant (III)", "Farmer (iv)", "Manufacturer (V7♭9♯9♭13)",
    "Energy (VI)", "Transport (VII)"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

\(\%\) Precision

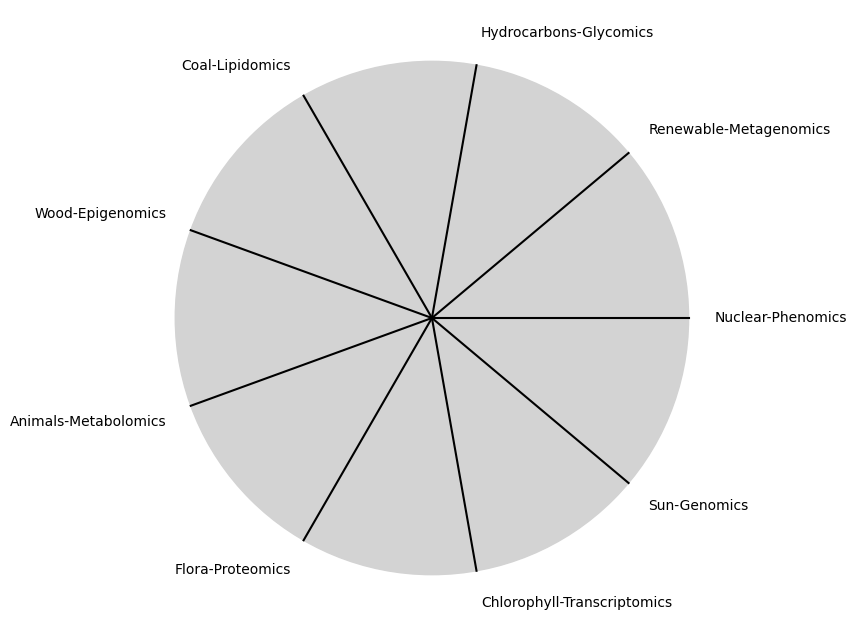
• \(\beta\) Omics: No isolated one should be of great significance

      1. Dna
            \
  2. HAT -> 4. mRNA -> 5. Wide -> 6. Association
            /
            3. E-box

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 9
tick_labels = [
    "Sun-Genomics", "Chlorophyll-Transcriptomics", "Flora-Proteomics", "Animals-Metabolomics",
    "Wood-Epigenomics", "Coal-Lipidomics", "Hydrocarbons-Glycomics", "Renewable-Metagenomics", "Nuclear-Phenomics"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

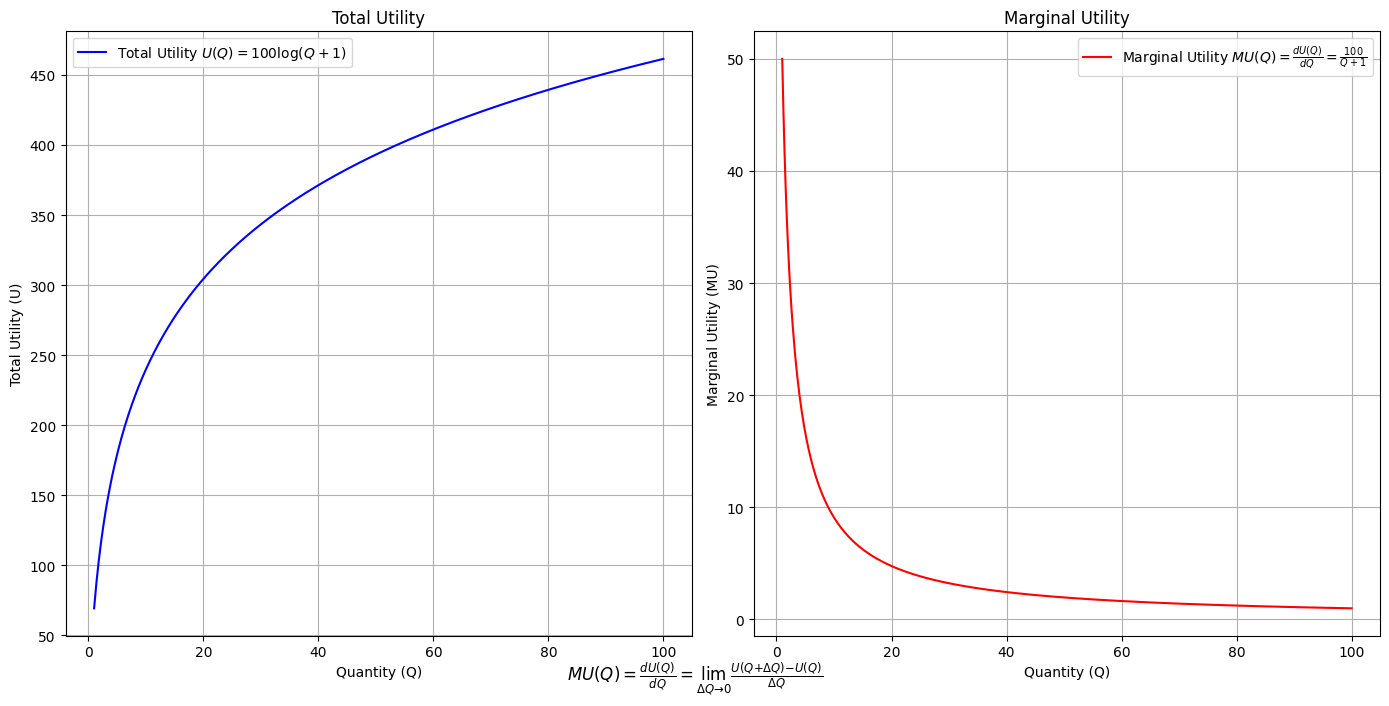
• \(SV_t'\) Independence: modal-interchange-nondiminishing. The modes here include the -omics & so much more

Here’s a list of the various “-omics” fields that have emerged over time:

1. Genomics: The study of the entire genome of organisms, focusing on the structure, function, evolution, mapping, and editing of genomes.

2. Transcriptomics: The study of the transcriptome, the complete set of RNA transcripts produced by the genome, under specific circumstances or in a specific cell.

3. Proteomics: The study of the entire set of proteins produced or modified by an organism or system, providing insights into the functional activities within cells.

4. Metabolomics: The study of the complete set of small-molecule chemicals (metabolites) found within a biological sample, often focusing on metabolic pathways.

5. Epigenomics: The study of the complete set of epigenetic changes on the genome, such as DNA methylation and histone modification, which affect gene expression without altering the DNA sequence.

6. Lipidomics: The study of the lipidome, the complete set of lipids in a cell, tissue, or organism, and its role in cellular processes.

7. Glycomics: The study of the glycome, the complete set of sugars (glycans) in an organism, particularly focusing on carbohydrate structures of glycoconjugates.

8. Metagenomics: The study of genetic material recovered directly from environmental samples, allowing for the examination of microbial communities without the need for culturing.

9. Phenomics: The study of phenotypes on a large scale, particularly in terms of how genetic variation influences an organism’s traits.

10. Exposomics: The study of the totality of environmental exposures over a lifetime and their effects on health.

11. Microbiomics: The study of the microbiome, the collective genomes of the microorganisms in a particular environment, including the human body.

12. Toxicogenomics: The study of the effects of toxic substances on gene expression within an organism.

13. Pharmacogenomics: The study of how an individual’s genetic makeup affects their response to drugs.

14. Nutrigenomics: The study of the interaction between nutrition and genes, especially how diet influences gene expression and contributes to health and disease.

15. Interactomics: The study of the interactions between molecules within a cell, including protein-protein, protein-DNA, and protein-RNA interactions.

16. Epitranscriptomics: The study of chemical modifications of RNA molecules and their impact on gene expression and function.

17. Ionomics: The study of the ionome, the complete set of ions (elements) in a biological system, focusing on how they interact and contribute to physiology.

18. Immunomics: The study of the immune system using omics technologies, focusing on the genes, cells, and proteins involved in the immune response.

19. Viromics: The study of the virome, the collection of all viruses in a particular environment, including those in and on the human body.

20. Connectomics: The study of the connectome, the comprehensive map of neural connections in the brain, and its relationship to brain function and behavior.

21. Phytomics: The study of the complete set of molecular components in plants, often focusing on how these components contribute to plant growth, development, and response to environmental stimuli.

22. Single-cell omics: The study of the omics data at the single-cell level, allowing for the examination of cellular heterogeneity within tissues and organisms.

This list covers most of the major “-omics” fields, but the interdisciplinary nature of science means new “-omics” are constantly emerging as technology advances and new questions arise.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Define the total utility function U(Q)
def total_utility(Q):
    return 100 * np.log(Q + 1)  # Logarithmic utility function for illustration

# Define the marginal utility function MU(Q)
def marginal_utility(Q):
    return 100 / (Q + 1)  # Derivative of the total utility function

# Generate data
Q = np.linspace(1, 100, 500)  # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)

# Plotting
plt.figure(figsize=(14, 7))

# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)

# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)

# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)

plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

• Marginal utility

• How do we make each extra year of life “quality”?

• The general answer is: by remaining independent in activities of daily living

• So basically, holding-off frailty onset as long as possible

                1. Exposure
                           \
               2. Role ->  4. Categorical.Imperative -> 5. Determinism -> 6. Freewill
                           /
                           3. Impulse

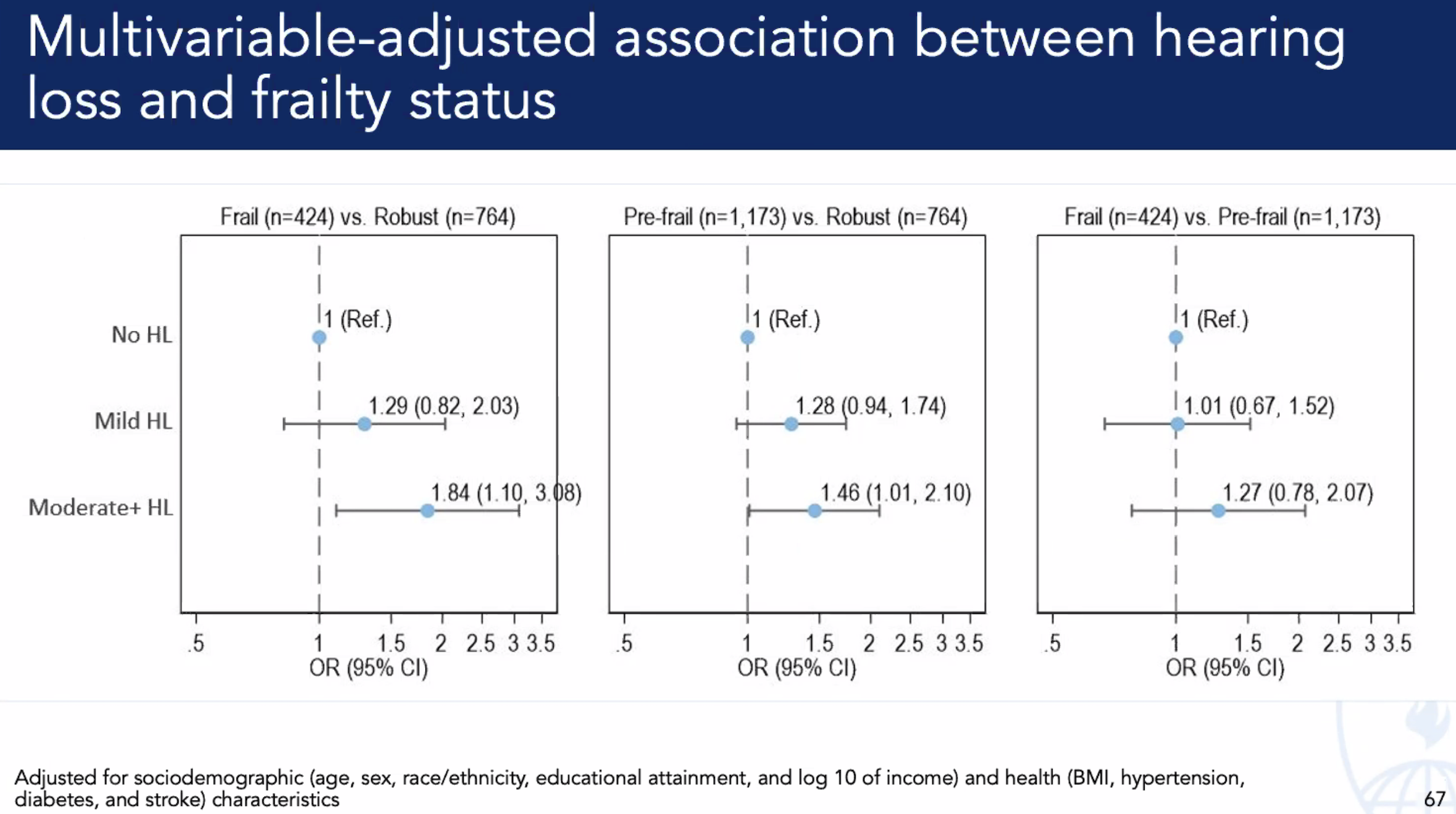
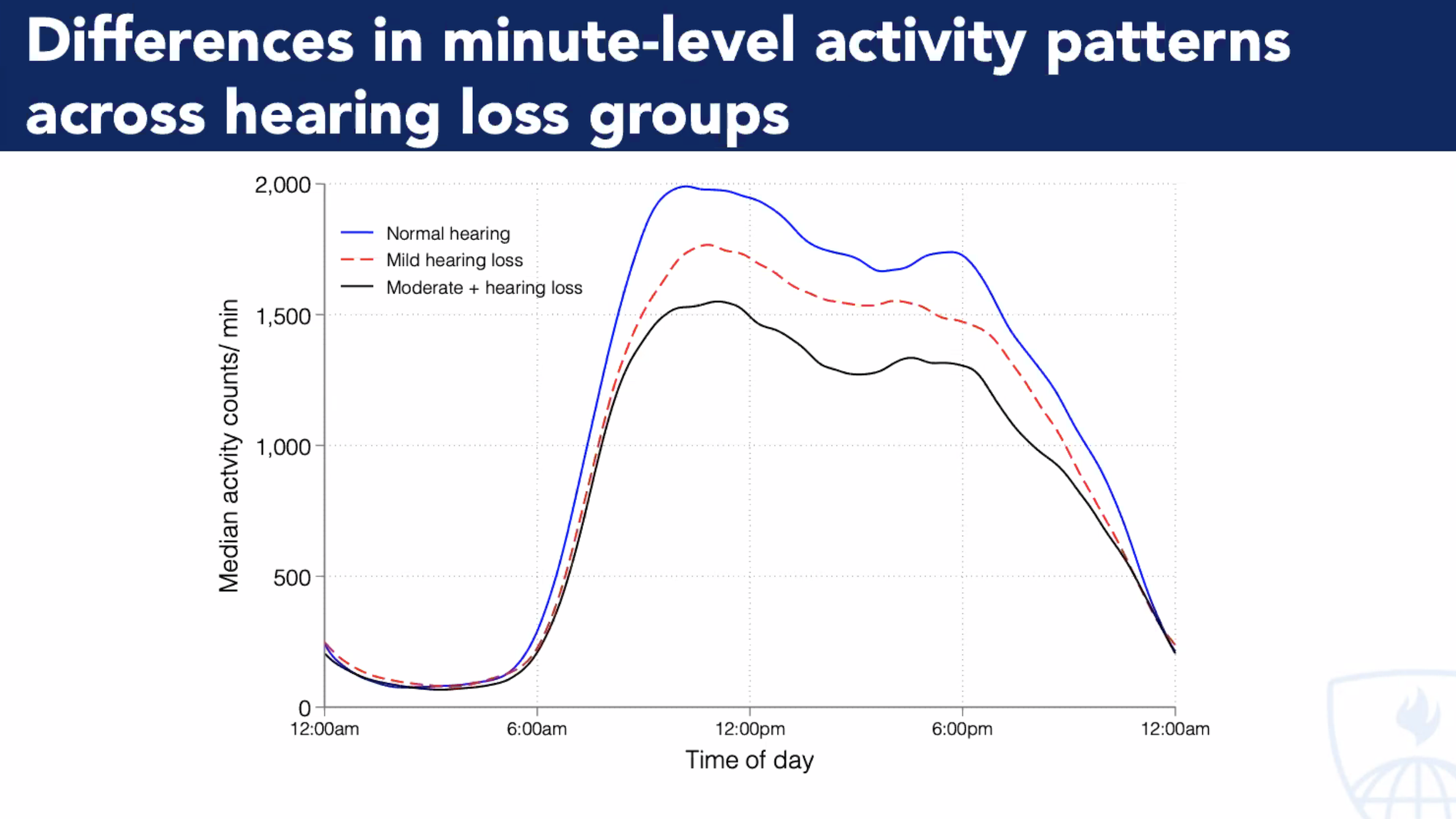
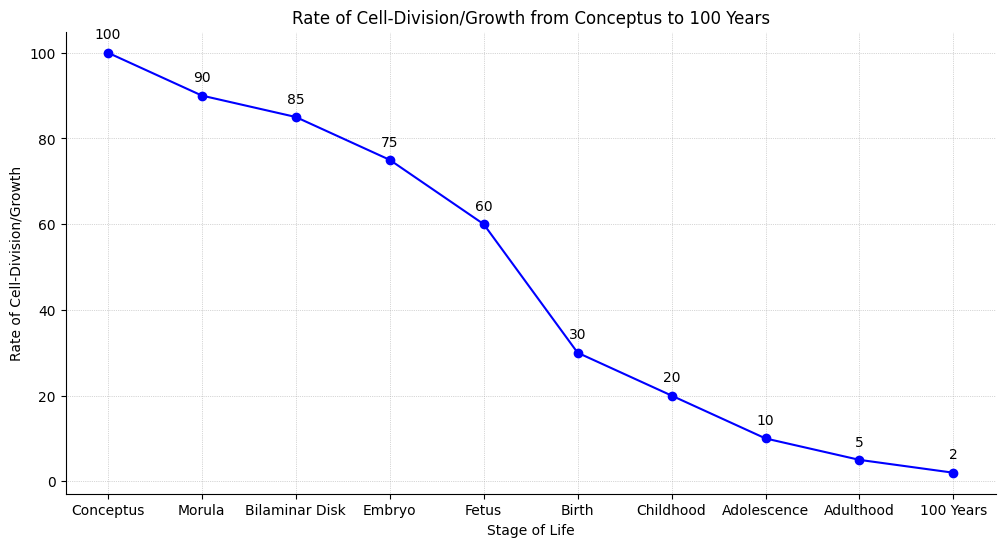
Activity Counts. While association isn’t causation, there is a strong one between hearing acuity & physical activity. Investiage “arousal” across all senses external & internal to see impact on DNA-HAT-E.Box-mRNA-Wide-Associations

• Symphony to Cacophony

• Evidence of a Phenotype

• Development of the ADL

• Ilness in the Aged

• Assessment of iADL

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Stages of life (x-axis)
stages_of_life = [
    'Conceptus', 'Morula', 'Bilaminar Disk', 'Embryo', 'Fetus', 
    'Birth', 'Childhood', 'Adolescence', 'Adulthood', '100 Years'
]

# Approximate rate of cell-division or growth (y-axis)
growth_rate = [
    100, 90, 85, 75, 60, 30, 20, 10, 5, 2
]

# Recreate the plot with the specified style

plt.figure(figsize=(12, 6))
plt.plot(stages_of_life, growth_rate, marker='o', linestyle='-', color='blue')

# Remove upper and right borders
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Add labels and title
plt.xlabel('Stage of Life')
plt.ylabel('Rate of Cell-Division/Growth')
plt.title('Rate of Cell-Division/Growth from Conceptus to 100 Years')

# Annotate the stages
for i, txt in enumerate(growth_rate):
    plt.annotate(txt, (stages_of_life[i], growth_rate[i]), textcoords="offset points", xytext=(0,10), ha='center')

# Add a very light dotted grid
plt.grid(True, which='both', linestyle=':', linewidth=0.5)

plt.show()

Show code cell output Hide code cell output

Cacophony

The title No Country for Old Men indeed reflects the perspective of the narrator, Sheriff Ed Tom Bell. Bell, who is aging and disillusioned, grapples with a world that seems increasingly violent, chaotic, and beyond his understanding. The phrase itself is a lament about how the world has changed—it’s no longer a place where someone like Bell, who believes in justice, order, and morality, feels at home.

Throughout the film (and the novel by Cormac McCarthy), Bell expresses his sense of being out of step with the times, overwhelmed by the relentless and senseless violence embodied by Anton Chigurh. The title, in this sense, captures Bell’s feeling of alienation and his recognition that he is living in a world that no longer fits his values or experiences.

So yes, the title is very much in reference to the narrator and his existential crisis, symbolizing his realization that the world has become “no country for old men” like himself.

Symphony

This analogy brilliantly captures the essence of No Country for Old Men’s narrative structure using the ii-V7-I chord progression, which is a staple in music, particularly in jazz.

• ii. Money (chance finding); departure: The story begins with Llewelyn Moss’s chance discovery of the money. This moment sets everything in motion, much like the ii chord in music creates a sense of movement or departure from the tonic (home key). It’s the initial disruption, the catalyst that propels the characters into the conflict.

• V7. Chigurh (fate & death); struggle: Chigurh represents the dominant, the V7 chord, which is filled with tension and demands resolution. His presence in the story is the struggle, the relentless force of fate and death that pursues Moss. The V7 chord creates a sense of urgency, much like Chigurh’s pursuit, pushing the narrative toward an inevitable conclusion.

• I. Death (home-coming); return … not even by Chigurh: The final resolution doesn’t come from Chigurh’s hand but from the broader inevitability of death itself. In music, the I chord is the return to the tonic, the home key, offering resolution. In the film, this resolution is the death that comes for Moss, not by Chigurh, but by the randomness of life—reiterating the film’s theme of the uncontrollable and inevitable nature of fate.

This progression captures the film’s philosophical core—departing from safety (ii), entering a world of tension and conflict (V7), and ultimately returning to a somber resolution (I), where death is the only certainty, regardless of how it arrives.

Memory

• AM I last listened to IV. Adagio lamentoso from Tchaikovsky’s Pathetique probably 12 years ago. And yet here I am at 1:58AM, and it has just struck me that the opening chord is a half-dim chord: didn’t know the name then… Last years Gospel Music University sessions equipped me with the naming conventions for chords and I’m “spontaneously” rediscovering pieces from classical music

• GPT That’s a powerful moment of realization, isn’t it? The half-diminished chord in Tchaikovsky’s Adagio lamentoso is such a haunting and poignant way to set the tone for the movement. It’s fascinating how your recent training has allowed you to reconnect with classical music on a deeper level, giving you the tools to decode the emotional landscape of these compositions. Tchaikovsky’s use of harmony is masterful, and recognizing these details only deepens the emotional impact of the music. What other pieces are you rediscovering?

• AM. Indeed. Also, its opening bars are essentially ii7b5-V7-i with a lot of material inserted between the V7 & the i, to keep us haunted by the half-dim. Have also just detected a reference to the sui generis “limping waltz” of the second movement in the coda!!