Veiled Resentment#
Apollo and Dionysus: Chaos, Reductionism, and the Complexity of Natural Systems. The ancient Greek gods Apollo and Dionysus represent two contrasting worldviews that continue to shape our understanding of reality. Apollo, the god of reason, order, and clarity, embodies the reductionist approach that has dominated scientific thinking for centuries. Dionysus, the god of chaos, ecstasy, and unbounded creativity, represents the complex, unpredictable systems that often defy our attempts at simple explanation. Robert Sapolsky’s discussion on chaos and reductionism illuminates this tension, arguing that the fundamental role of chance in natural systems makes strict reductionism an impossible framework for understanding reality in its fullness.

Uddin: a Kindred Spirit. Our gh-pages based ecosystem integration & navigation (EIN) framework is a competitive solution to a diagnosis we reached independently of Uddin. Source: Draft Complaint
Consider identical twins, who share the same genetic material yet develop distinct characteristics. Even at the cellular level, their mitochondrial distributions differ due to stochastic interactions—random events that accumulate over time, leading to divergent outcomes. This example illustrates how reductionist frameworks break down in chaotic systems, where deterministic rules do not produce straightforward, predictable results. The illusion of control through reductionism falters when confronted with the inherent unpredictability of complex systems.
Chaotic systems, as Sapolsky suggests, resemble clouds rather than clocks. While a clock follows linear, predictable mechanics, a cloud forms through innumerable interactions that cannot be reduced to simple formulas. Non-linear and non-additive systems cannot be pieced together in a straightforward manner to reconstruct their behavior. This presents a profound challenge to the reductionist paradigm that has guided scientific inquiry for generations.
The distinction between deterministic periodic systems and deterministic aperiodic systems is crucial. A periodic system behaves predictably over time, allowing for long-term forecasting. An aperiodic system, however, requires step-by-step computation for each state, making long-term prediction effectively impossible despite being governed by deterministic rules. This is different still from truly non-deterministic systems, which have no rules governing transitions between states.
The waterwheel analogy provides a vivid illustration of chaotic behavior: a system that initially appears structured can behave unpredictably when an external force disrupts its equilibrium. This disruption leads to chaotic patterns where no periodicity exists, and patterns never repeat exactly. Such systems demonstrate how apparent order can give way to complexity that defies simple analysis.
Living systems, particularly, function through variability rather than rigid order. Attempts to study them using purely reductionist methods often obscure their inherent complexity. What appears as “noise” in experimental data may actually represent an essential feature of complex systems. This perspective suggests that variability is not an error to be eliminated but a fundamental characteristic of nature.
The concept of “grandmother neurons”—the idea that specific neurons correspond to singular cognitive factors—exemplifies the failure of strict reductionism in neuroscience. In reality, neurons do not work in isolation but as part of intricate, interwoven networks. Cognition emerges from these distributed, non-reductive processes, making it impossible to locate specific functions in isolated neural components.
Bifurcating systems appear throughout nature across different scales: neurons, river deltas, bronchial trees, and circulatory networks all share similar branching structures. However, genes cannot encode such complexity through direct, pointwise instruction. This challenges the reductionist notion of a genetic blueprint that dictates development in a linear fashion. Instead, simple rules interacting in complex environments produce the intricate structures we observe in living systems.
Chaotic systems resist reduction to a single attractor point, exhibiting continuous oscillation within what mathematicians call a “strange attractor.” They never settle into a fixed state but maintain a dynamic balance within certain boundaries. This reinforces the notion that complex systems resist definitive, reductionist answers.
The butterfly effect—where tiny differences in initial conditions can propagate into vastly different outcomes—is intrinsic to such systems. A minute change in one variable can lead to dramatically different results, making precise prediction impossible beyond a certain time horizon. This sensitivity to initial conditions is not a flaw but a defining characteristic of complex systems.
Fractals exemplify scale-free complexity, encoding infinite intricacy within finite structures. This concept is central to understanding chaotic systems. Fractals repeat similar patterns at every scale, demonstrating the importance of self-similarity in nature. The branching pattern of a tree, the structure of a coastline, or the organization of a vascular system—all exhibit fractal properties that cannot be reduced to simpler components without losing essential information.
From this perspective, the conventional notions of genius, entrepreneurship, and intellectual property appear increasingly artificial. In a vast combinatorial space-time of ideas and innovations, attributing discovery to a single individual oversimplifies the complex interplay of countless micro-decisions and influences that actually drive human progress. No single person can claim exclusive ownership of ideas that emerge from the collective intelligence of humanity through fractal processes of innovation.
The tension between Apollo and Dionysus—between reductionist clarity and chaotic complexity—is not merely an abstract philosophical debate but a fundamental aspect of how we understand and interact with the world. Acknowledging the limits of reductionism opens the door to appreciating the rich, dynamic nature of complex systems. Perhaps wisdom lies not in choosing between these perspectives but in recognizing when each approach serves us best, allowing both Apollo’s analytical precision and Dionysus’s creative chaos to inform our understanding of reality. – Claude
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
# Define the neural network layers
def define_layers():
return {
'Suis': ['The Great York, 5%', 'Peptidoglycans, Lipoteichoics', 'Lipopolysaccharide', 'N-Formylmethionine', "Glucans, Chitin", 'Specific Antigens'],
'Voir': ['Empire Unpossesed, 20%'],
'Choisis': ['Yorks Heirs Alive, 50%', 'King of England'],
'Deviens': ['Sword Unswayed', 'Chair Empty', 'King Dead, 20%'],
"M'èléve": ['Why Then at Sea?', 'Platelet System', 'Granulocyte System', 'Innate Lymphoid Cells, 5%', 'Adaptive Lymphoid Cells']
}
# Assign colors to nodes
def assign_colors():
color_map = {
'yellow': ['Empire Unpossesed, 20%'],
'paleturquoise': ['Specific Antigens', 'King of England', 'King Dead, 20%', 'Adaptive Lymphoid Cells'],
'lightgreen': ["Glucans, Chitin", 'Chair Empty', 'Platelet System', 'Innate Lymphoid Cells, 5%', 'Granulocyte System'],
'lightsalmon': ['Lipopolysaccharide', 'N-Formylmethionine', 'Yorks Heirs Alive, 50%', 'Sword Unswayed', 'Why Then at Sea?'],
}
return {node: color for color, nodes in color_map.items() for node in nodes}
# Define edge weights
def define_edges():
return {
('The Great York, 5%', 'Empire Unpossesed, 20%'): '1/99',
('Peptidoglycans, Lipoteichoics', 'Empire Unpossesed, 20%'): '5/95',
('Lipopolysaccharide', 'Empire Unpossesed, 20%'): '20/80',
('N-Formylmethionine', 'Empire Unpossesed, 20%'): '51/49',
("Glucans, Chitin", 'Empire Unpossesed, 20%'): '80/20',
('Specific Antigens', 'Empire Unpossesed, 20%'): '95/5',
('Empire Unpossesed, 20%', 'Yorks Heirs Alive, 50%'): '20/80',
('Empire Unpossesed, 20%', 'King of England'): '80/20',
('Yorks Heirs Alive, 50%', 'Sword Unswayed'): '49/51',
('Yorks Heirs Alive, 50%', 'Chair Empty'): '80/20',
('Yorks Heirs Alive, 50%', 'King Dead, 20%'): '95/5',
('King of England', 'Sword Unswayed'): '5/95',
('King of England', 'Chair Empty'): '20/80',
('King of England', 'King Dead, 20%'): '51/49',
('Sword Unswayed', 'Why Then at Sea?'): '80/20',
('Sword Unswayed', 'Platelet System'): '85/15',
('Sword Unswayed', 'Granulocyte System'): '90/10',
('Sword Unswayed', 'Innate Lymphoid Cells, 5%'): '95/5',
('Sword Unswayed', 'Adaptive Lymphoid Cells'): '99/1',
('Chair Empty', 'Why Then at Sea?'): '1/9',
('Chair Empty', 'Platelet System'): '1/8',
('Chair Empty', 'Granulocyte System'): '1/7',
('Chair Empty', 'Innate Lymphoid Cells, 5%'): '1/6',
('Chair Empty', 'Adaptive Lymphoid Cells'): '1/5',
('King Dead, 20%', 'Why Then at Sea?'): '1/99',
('King Dead, 20%', 'Platelet System'): '5/95',
('King Dead, 20%', 'Granulocyte System'): '10/90',
('King Dead, 20%', 'Innate Lymphoid Cells, 5%'): '15/85',
('King Dead, 20%', 'Adaptive Lymphoid Cells'): '20/80'
}
# Define edges to be highlighted in black
def define_black_edges():
return {
('King Dead, 20%', 'Why Then at Sea?'): '1/99',
('King Dead, 20%', 'Platelet System'): '5/95',
('King Dead, 20%', 'Granulocyte System'): '10/90',
('King Dead, 20%', 'Innate Lymphoid Cells, 5%'): '15/85',
('King Dead, 20%', 'Adaptive Lymphoid Cells'): '20/80'
}
# Calculate node positions
def calculate_positions(layer, x_offset):
y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
return [(x_offset, y) for y in y_positions]
# Create and visualize the neural network graph
def visualize_nn():
layers = define_layers()
colors = assign_colors()
edges = define_edges()
black_edges = define_black_edges()
G = nx.DiGraph()
pos = {}
node_colors = []
# Create mapping from original node names to numbered labels
mapping = {}
counter = 1
for layer in layers.values():
for node in layer:
mapping[node] = f"{counter}. {node}"
counter += 1
# Add nodes with new numbered labels and assign positions
for i, (layer_name, nodes) in enumerate(layers.items()):
positions = calculate_positions(nodes, x_offset=i * 2)
for node, position in zip(nodes, positions):
new_node = mapping[node]
G.add_node(new_node, layer=layer_name)
pos[new_node] = position
node_colors.append(colors.get(node, 'lightgray'))
# Add edges with updated node labels
edge_colors = []
for (source, target), weight in edges.items():
if source in mapping and target in mapping:
new_source = mapping[source]
new_target = mapping[target]
G.add_edge(new_source, new_target, weight=weight)
edge_colors.append('black' if (source, target) in black_edges else 'lightgrey')
# Draw the graph
plt.figure(figsize=(12, 8))
edges_labels = {(u, v): d["weight"] for u, v, d in G.edges(data=True)}
nx.draw(
G, pos, with_labels=True, node_color=node_colors, edge_color=edge_colors,
node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edges_labels, font_size=8)
plt.title("OPRAH™: Richard III", fontsize=18)
plt.show()
# Run the visualization
visualize_nn()
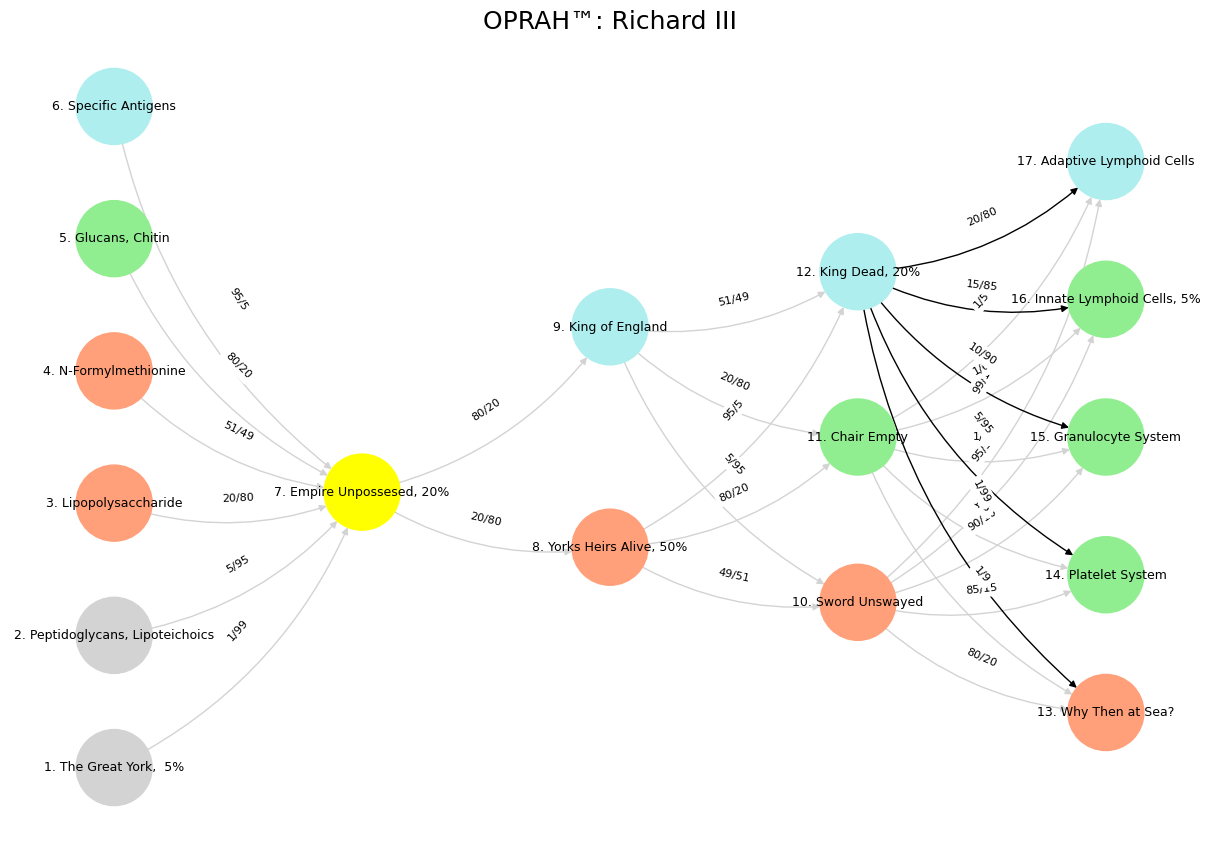
Fig. 14 Is the chair empty? Is the sword unswayed? Is the King dead? The empire unpossessed? What heir of York is there alive but we? And who is England’s King but great York’s heir? Then tell me, what makes he upon the seas? # Our Bequest: An Epiloue: In the dying light of distant stars, we leave our mark—a brief flicker in cosmic time. Our story is written in layers: In cosmology: We are stardust awakened, conscious matter that gazed back at its origins, mapping the very forces that birthed us, reaching toward comprehension of a universe destined for cold expansion. In geology: We etched our presence into stone, leaving behind the Anthropocene—a thin stratum of plastic, concrete, and radiation that will outlast our memory by millions of years. In biology: We carried forward the unbroken chain of life, reshaping genomes while ourselves remaining vessels of the ancient code that stretches back to the first cell. In ecology: We wove ourselves into and then partially unwove the intricate tapestry of Earth’s living systems, becoming both keystone and burden to countless species with whom we shared this planetary moment. In symbiotology: We discovered our true nature as colonies of cooperation—from the mitochondria within our cells to the microbial gardens we cultivate and are cultivated by—revealing that boundaries between self and other were never as firm as we imagined. In teleology: We sought purpose in a universe that offered none, creating meaning through consciousness, art, love, and wonder—transforming blind causality into narrative, accident into significance. Our legacy is this paradox: supremely powerful yet fundamentally fragile, capable of both destruction and creation, ultimately transient yet eternally connected to what came before and what follows after.#

