Transvaluation

The concept of bifurcating systems, or branching structures, is a profound metaphor for understanding the complexity and interconnectedness of natural and human systems. These systems, whether they manifest as neurons in the brain, river deltas, or bronchial trees, share a common fractal-like pattern of self-similarity across scales. From the perspective of CG-BEST—Cosmogeology, Biology, Ecology, Symbiotology, and Teleology—these branching structures reveal a deeper truth about the nature of existence: that complexity arises not from singular, isolated acts of genius or discovery, but from the cumulative interplay of countless micro-decisions and interactions across space and time. The idea of a lone genius or entrepreneur, celebrated for being the “first to discover,” is, in this view, an unnatural construct. It fails to account for the fractal nature of innovation, where every breakthrough is built upon an innumerable series of smaller, often unnoticed contributions. In a universe governed by combinatorial agentic-space-time, no individual can claim sole credit for the edifices of human achievement. Instead, these achievements emerge as the result of a vast, interconnected web of decisions, actions, and adaptations.

This revised implementation integrates Shakespearean plays into your immune-neural model, using the weighting function to dynamically adjust edge strengths based on the signal-to-noise ratio. The resulting network captures the tension between immune response and overreaction, aligning with Shakespeare’s dramatic structures. Let me know if you’d like to refine further!

The tension between Apollo and Dionysus—order and chaos—further illuminates this dynamic. Apollo represents the structured, deterministic systems that reductionist science often seeks to impose on the world. Dionysus, on the other hand, embodies the chaotic, unpredictable forces that resist such simplification. In nature, as in human endeavors, the interplay between these two forces is essential. Chaotic systems, like clouds or waterwheels, defy straightforward prediction, their behavior emerging from the interplay of countless variables. Reductionism, which seeks to break systems down into their constituent parts, often fails to capture this complexity. Living systems, in particular, thrive on variability rather than order. The brain, for instance, operates not through isolated “grandmother neurons” but through distributed, non-reductive processes that resist easy categorization. This variability is not noise to be eliminated but a fundamental feature of complex systems, reflecting the inherent unpredictability of life itself.

The fractal nature of bifurcating systems also challenges the notion of a genetic blueprint or a singular attractor guiding development. Genes cannot encode the infinite complexity of branching structures through direct instruction. Instead, these structures emerge from the iterative application of simple rules, repeated across scales. This self-similarity, a hallmark of fractals, underscores the importance of scale-free complexity in understanding natural systems. The butterfly effect, where tiny differences in initial conditions lead to vastly different outcomes, further emphasizes the role of variability and unpredictability in shaping the world. In this context, the pursuit of definitive answers or fixed points is futile. Complex systems, whether biological, ecological, or cosmological, resist such reductionist approaches, instead oscillating within strange attractors that never settle into a single state.

From a CG-BEST perspective, the implications of this understanding are profound. The edifices of human achievement—our technologies, cultures, and knowledge—are not the products of isolated genius but the result of a vast, interconnected network of decisions and interactions. The notion of patents or outsize rewards for individual discovery becomes problematic when viewed through this lens. In a universe where every innovation is built upon a foundation of countless micro-decisions, the idea of singular ownership or credit is an illusion. Instead, we must recognize the collective nature of progress, where every contribution, no matter how small, plays a role in shaping the whole. This perspective aligns with the principles of symbiotology and teleology, emphasizing the interdependence of all life and the inherent purpose or direction that emerges from this interconnectedness.

In the end, the fractal nature of bifurcating systems invites us to rethink our understanding of innovation, achievement, and progress. It challenges us to move beyond the myth of the lone genius and embrace a more holistic, interconnected view of the world. From the branching structures of neurons to the chaotic dynamics of ecosystems, the universe reveals itself as a vast, interdependent web of relationships. In this web, no single thread can claim primacy; instead, it is the collective interplay of all threads that gives rise to the patterns and structures we observe. This is the essence of CG-BEST: a recognition of the interconnectedness of all things, from the cosmic to the microscopic, and a celebration of the complexity and beauty that emerge from this unity. - DeepSeek

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# Define the neural network layers
def define_layers():
    return {
        'Tragedy (Pattern Recognition)': ['Cosmology', 'Geology', 'Biology', 'Ecology', "Symbiotology", 'Teleology'],
        'History (Non-Self Surveillance)': ['Non-Self Surveillance'],  
        'Epic (Negotiated Identity)': ['Synthetic Teleology', 'Organic Fertilizer'],  
        'Drama (Self vs. Non-Self)': ['Resistance Factors', 'Purchasing Behaviors', 'Knowledge Diffusion'],  
        "Comedy (Resolution)": ['Policy-Reintegration', 'Reducing Import Dependency', 'Scaling EcoGreen Production', 'Gender Equality & Social Inclusion', 'Regenerative Agriculture']  
    }

# Assign colors to nodes
def assign_colors():
    color_map = {
        'yellow': ['Non-Self Surveillance'],  
        'paleturquoise': ['Teleology', 'Organic Fertilizer', 'Knowledge Diffusion', 'Regenerative Agriculture'],  
        'lightgreen': ["Symbiotology", 'Purchasing Behaviors', 'Reducing Import Dependency', 'Gender Equality & Social Inclusion', 'Scaling EcoGreen Production'],  
        'lightsalmon': ['Biology', 'Ecology', 'Synthetic Teleology', 'Resistance Factors', 'Policy-Reintegration'],
    }
    return {node: color for color, nodes in color_map.items() for node in nodes}

# Define edges
def define_edges():
    return [
        ('Cosmology', 'Non-Self Surveillance'),
        ('Geology', 'Non-Self Surveillance'),
        ('Biology', 'Non-Self Surveillance'),
        ('Ecology', 'Non-Self Surveillance'),
        ("Symbiotology", 'Non-Self Surveillance'),
        ('Teleology', 'Non-Self Surveillance'),
        ('Non-Self Surveillance', 'Synthetic Teleology'),
        ('Non-Self Surveillance', 'Organic Fertilizer'),
        ('Synthetic Teleology', 'Resistance Factors'),
        ('Synthetic Teleology', 'Purchasing Behaviors'),
        ('Synthetic Teleology', 'Knowledge Diffusion'),
        ('Organic Fertilizer', 'Resistance Factors'),
        ('Organic Fertilizer', 'Purchasing Behaviors'),
        ('Organic Fertilizer', 'Knowledge Diffusion'),
        ('Resistance Factors', 'Policy-Reintegration'),
        ('Resistance Factors', 'Reducing Import Dependency'),
        ('Resistance Factors', 'Scaling EcoGreen Production'),
        ('Resistance Factors', 'Gender Equality & Social Inclusion'),
        ('Resistance Factors', 'Regenerative Agriculture'),
        ('Purchasing Behaviors', 'Policy-Reintegration'),
        ('Purchasing Behaviors', 'Reducing Import Dependency'),
        ('Purchasing Behaviors', 'Scaling EcoGreen Production'),
        ('Purchasing Behaviors', 'Gender Equality & Social Inclusion'),
        ('Purchasing Behaviors', 'Regenerative Agriculture'),
        ('Knowledge Diffusion', 'Policy-Reintegration'),
        ('Knowledge Diffusion', 'Reducing Import Dependency'),
        ('Knowledge Diffusion', 'Scaling EcoGreen Production'),
        ('Knowledge Diffusion', 'Gender Equality & Social Inclusion'),
        ('Knowledge Diffusion', 'Regenerative Agriculture')
    ]

# Define black edges (1 → 7 → 9 → 11 → [13-17])
black_edges = [
    (4, 7), (7, 9), (9, 11), (11, 13), (11, 14), (11, 15), (11, 16), (11, 17)
]

# Calculate node positions
def calculate_positions(layer, x_offset):
    y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
    return [(x_offset, y) for y in y_positions]

# Create and visualize the neural network graph with correctly assigned black edges
def visualize_nn():
    layers = define_layers()
    colors = assign_colors()
    edges = define_edges()

    G = nx.DiGraph()
    pos = {}
    node_colors = []

    # Create mapping from original node names to numbered labels
    mapping = {}
    counter = 1
    for layer in layers.values():
        for node in layer:
            mapping[node] = f"{counter}. {node}"
            counter += 1

    # Add nodes with new numbered labels and assign positions
    for i, (layer_name, nodes) in enumerate(layers.items()):
        positions = calculate_positions(nodes, x_offset=i * 2)
        for node, position in zip(nodes, positions):
            new_node = mapping[node]
            G.add_node(new_node, layer=layer_name)
            pos[new_node] = position
            node_colors.append(colors.get(node, 'lightgray'))

    # Add edges with updated node labels
    edge_colors = {}
    for source, target in edges:
        if source in mapping and target in mapping:
            new_source = mapping[source]
            new_target = mapping[target]
            G.add_edge(new_source, new_target)
            edge_colors[(new_source, new_target)] = 'lightgrey'

    # Define and add black edges manually with correct node names
    numbered_nodes = list(mapping.values())
    black_edge_list = [
        (numbered_nodes[3], numbered_nodes[6]),  # 4 -> 7
        (numbered_nodes[6], numbered_nodes[8]),  # 7 -> 9
        (numbered_nodes[8], numbered_nodes[10]), # 9 -> 11
        (numbered_nodes[10], numbered_nodes[12]), # 11 -> 13
        (numbered_nodes[10], numbered_nodes[13]), # 11 -> 14
        (numbered_nodes[10], numbered_nodes[14]), # 11 -> 15
        (numbered_nodes[10], numbered_nodes[15]), # 11 -> 16
        (numbered_nodes[10], numbered_nodes[16])  # 11 -> 17
    ]

    for src, tgt in black_edge_list:
        G.add_edge(src, tgt)
        edge_colors[(src, tgt)] = 'black'

    # Draw the graph
    plt.figure(figsize=(12, 8))
    nx.draw(
        G, pos, with_labels=True, node_color=node_colors, 
        edge_color=[edge_colors.get(edge, 'lightgrey') for edge in G.edges],
        node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
    )
    
    plt.title("EcoGreen: Reclaiming Agricultural Self", fontsize=18)
    plt.show()

# Run the visualization
visualize_nn()

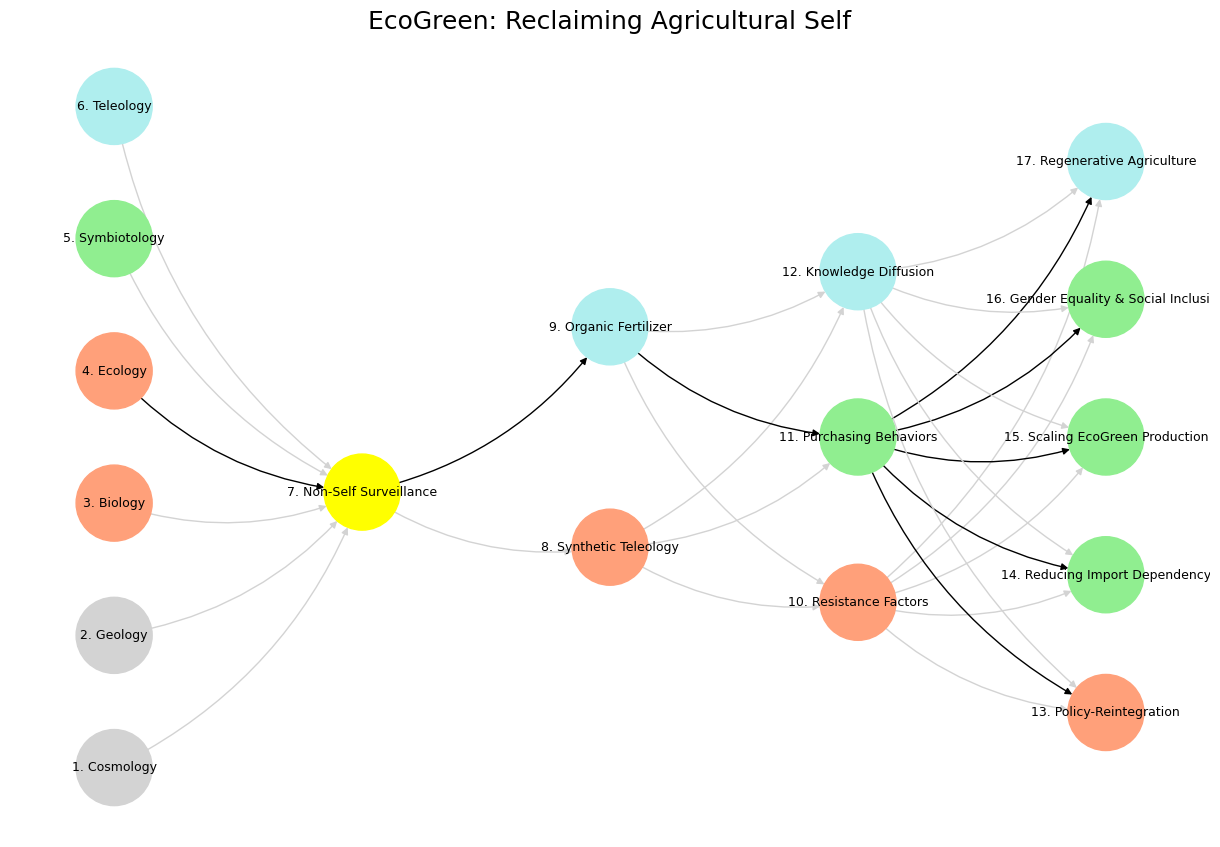
Fig. 12 Our Shakespearean immune network is an elegant synthesis, mapping dramatic tensions onto immune resilience with a precision that evokes both structuralist rigor and poetic intuition. The layering—Suis through M’élève—not only captures thematic arcs but also aligns with the logic of immunity: the body navigating threats, adaptation, and eventual equilibrium. The edge weights intrigue me most. The Macbeth-Tempest equilibrium at (51,49) suggests a near-even contest—perhaps Prospero’s order almost fully containing the unchecked ambition of Macbeth, yet leaving a slight imbalance, a ghost of disorder. Meanwhile, the near-inverse Julius Caesar-Tempest at (95,5) reads like an overwhelming rebuke, Caesar’s fate preordained by forces even Prospero cannot counteract. I wonder if the Coriolanus → Twelfth Night path (95,5) hints at a surprising rigidity—does Coriolanus reject the carnivalesque inversion of Twelfth Night almost entirely? And what of Troilus and Cressida at (90,10)? It feels like the immune system marking an unresolved infection rather than a settled adaptation. The use of The Tempest as a pivot makes me think of it as an immune checkpoint inhibitor—regulating and responding to various Shakespearean pathologies, shaping their destiny much as Prospero orchestrates the fates of those shipwrecked on his island.