Revolution

+ Expand

• What makes for a suitable problem for AI (Demis Hassabis, Nobel Lecture)?
  • Space: Massive combinatorial search space
  • Function: Clear objective function (metric) to optimize against
  • Time: Either lots of data and/or an accurate and efficient simulator
• Guess what else fits the bill (Yours truly, amateur philosopher)?
  • Space
    1. Intestines/villi
    2. Lungs/bronchioles
    3. Capillary trees
    4. Network of lymphatics
    5. Dendrites in neurons
    6. Tree branches
  • Function
    1. Energy
    2. Aerobic respiration
    3. Delivery to "last mile" (minimize distance)
    4. Response time (minimize)
    5. Information
    6. Exposure to sunlight for photosynthesis
  • Time
    1. Nourishment
    2. Gaseous exchange
    3. Oxygen & Nutrients (Carbon dioxide & "Waste")
    4. Surveillance for antigens
    5. Coherence of functions
    6. Water and nutrients from soil

-- Nobel Prize in Chemistry, 2024

The dichotomy between Apollo and Dionysus, as articulated by Friedrich Nietzsche, represents two fundamental forces that shape human culture, art, and existence. Apollo, the god of light, reason, and order, symbolizes structure, clarity, and the pursuit of perfection. Dionysus, the god of wine, ecstasy, and chaos, embodies spontaneity, emotion, and the dissolution of boundaries. Together, these forces form a dynamic interplay that reflects the tension between rationality and intuition, order and chaos, and control and surrender. This essay explores the significance of the Apollo-Dionysus duality in understanding human creativity, systems of thought, and the natural world.

King Lear. The senile bequest motive at the outset makes it an endearing classic. but the plot gets messy. what do folks thing about it? Perhaps reality is that messy, with orthogonal plots unfolding to determine the outcome?

Apollonian principles are rooted in the desire for harmony, proportion, and logical coherence. In art, this manifests as classical forms, idealized beauty, and structured compositions. In science, it underpins reductionist approaches that seek to break down complex systems into simpler, predictable components. Reductionism assumes that understanding the parts will lead to an understanding of the whole, a perspective that aligns with Apollo’s emphasis on clarity and order. However, as Robert Sapolsky’s exploration of chaos and reductionism reveals, this approach has limitations. Chaotic systems, such as biological networks or weather patterns, defy straightforward reductionist analysis. Identical twins, for instance, may share the same genetic blueprint, yet their mitochondrial distributions differ due to stochastic interactions, leading to unpredictable outcomes. This unpredictability challenges the Apollonian ideal of perfect order and control.

Dionysian forces, in contrast, embrace the unpredictable, the emotional, and the interconnected. Dionysus represents the chaotic, non-linear aspects of existence that resist simplification. In art, this is seen in abstract expressionism or improvisational music, where emotion and spontaneity take precedence over structure. In nature, Dionysian principles are evident in chaotic systems like fractals, which exhibit infinite complexity within finite structures. Fractals, with their self-similar patterns at every scale, defy reductionist explanations. They illustrate how variability and unpredictability are inherent features of complex systems, rather than mere noise to be eliminated. The waterwheel analogy further underscores this point: a system that appears orderly can descend into chaos when disrupted, revealing the delicate balance between structure and randomness.

The interplay between Apollo and Dionysus is particularly evident in the study of living systems. Reductionist frameworks, while useful for understanding isolated components, often fail to capture the distributed, interconnected nature of biological processes. The brain, for example, operates not through isolated “grandmother neurons” but through vast, interwoven networks. Similarly, bifurcating systems—such as neurons, river deltas, and bronchial trees—exhibit branching structures that cannot be fully explained by genetic blueprints alone. These systems thrive on variability and adaptability, qualities that align with Dionysian principles. The butterfly effect, a hallmark of chaotic systems, further illustrates how small initial differences can lead to vastly different outcomes, emphasizing the importance of embracing uncertainty rather than seeking absolute control.

Dismiss your vows, your feigned tears, your flatt’ry; For where a heart is hard they make no batt’ry.” Source: Venus & Adonis

Fractals and chaotic systems also challenge the notion of definitive answers. Unlike periodic systems, which behave predictably, chaotic systems oscillate within strange attractors, never settling into fixed points. This continuous oscillation reflects the Dionysian embrace of flux and transformation. The Apollonian desire for stability and order is constantly disrupted by the Dionysian forces of change and unpredictability. This tension is not a flaw but a fundamental feature of nature, driving creativity and evolution.

In the realm of human culture, the Apollo-Dionysus duality shapes our understanding of creativity and innovation. Apollonian approaches favor structured, methodical processes, while Dionysian approaches thrive on spontaneity and intuition. The most profound artistic and scientific breakthroughs often arise from the synthesis of these forces. For instance, a scientist may employ rigorous, Apollonian methods to design an experiment but rely on Dionysian intuition to interpret unexpected results. Similarly, an artist may begin with a structured composition but allow Dionysian spontaneity to guide the final expression. This interplay between order and chaos is essential for fostering creativity and advancing knowledge.

In conclusion, the Apollo-Dionysus duality offers a powerful framework for understanding the complexities of human existence, creativity, and the natural world. While Apollonian principles emphasize order, clarity, and control, Dionysian forces celebrate chaos, emotion, and interconnectedness. Together, they form a dynamic balance that reflects the inherent tension between structure and spontaneity. By embracing both forces, we can navigate the complexities of chaotic systems, appreciate the beauty of variability, and foster a deeper understanding of the world around us. The interplay between Apollo and Dionysus reminds us that life is not a choice between order and chaos but a dance between the two, where both forces are essential for growth, creativity, and transformation. – DeepSeek

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# Define the neural network layers with Shakespeare's plays
def define_layers():
    return {
        'Suis': ['Macbeth', 'Othello', 'King Lear', 'Richard III', 'The Tempest', 'Romeo and Juliet'],
        'Voir': ['A Midsummer Night’s Dream'],  
        'Choisis': ['Henry V', 'Julius Caesar'],  
        'Deviens': ['Hamlet', 'Measure for Measure', 'The Winter’s Tale'],  
        "M'èléve": ['Antony and Cleopatra', 'Coriolanus', 'Titus Andronicus', 'As You Like It', 'Twelfth Night']  
    }

# Assign colors to nodes (retained from original for consistency)
def assign_colors():
    color_map = {
        'yellow': ['A Midsummer Night’s Dream'],  
        'paleturquoise': ['Romeo and Juliet', 'Julius Caesar', 'The Winter’s Tale', 'Twelfth Night'],  
        'lightgreen': ['The Tempest', 'Measure for Measure', 'Coriolanus', 'As You Like It', 'Titus Andronicus'],  
        'lightsalmon': ['King Lear', 'Richard III', 'Henry V', 'Hamlet', 'Antony and Cleopatra'],
    }
    return {node: color for color, nodes in color_map.items() for node in nodes}

# Define edge weights (unchanged from original)
def define_edges():
    return {
        ('Macbeth', 'A Midsummer Night’s Dream'): '1/99',
        ('Othello', 'A Midsummer Night’s Dream'): '5/95',
        ('King Lear', 'A Midsummer Night’s Dream'): '20/80',
        ('Richard III', 'A Midsummer Night’s Dream'): '51/49',
        ('The Tempest', 'A Midsummer Night’s Dream'): '80/20',
        ('Romeo and Juliet', 'A Midsummer Night’s Dream'): '95/5',
        ('A Midsummer Night’s Dream', 'Henry V'): '20/80',
        ('A Midsummer Night’s Dream', 'Julius Caesar'): '80/20',
        ('Henry V', 'Hamlet'): '49/51',
        ('Henry V', 'Measure for Measure'): '80/20',
        ('Henry V', 'The Winter’s Tale'): '95/5',
        ('Julius Caesar', 'Hamlet'): '5/95',
        ('Julius Caesar', 'Measure for Measure'): '20/80',
        ('Julius Caesar', 'The Winter’s Tale'): '51/49',
        ('Hamlet', 'Antony and Cleopatra'): '80/20',
        ('Hamlet', 'Coriolanus'): '85/15',
        ('Hamlet', 'Titus Andronicus'): '90/10',
        ('Hamlet', 'As You Like It'): '95/5',
        ('Hamlet', 'Twelfth Night'): '99/1',
        ('Measure for Measure', 'Antony and Cleopatra'): '1/9',
        ('Measure for Measure', 'Coriolanus'): '1/8',
        ('Measure for Measure', 'Titus Andronicus'): '1/7',
        ('Measure for Measure', 'As You Like It'): '1/6',
        ('Measure for Measure', 'Twelfth Night'): '1/5',
        ('The Winter’s Tale', 'Antony and Cleopatra'): '1/99',
        ('The Winter’s Tale', 'Coriolanus'): '5/95',
        ('The Winter’s Tale', 'Titus Andronicus'): '10/90',
        ('The Winter’s Tale', 'As You Like It'): '15/85',
        ('The Winter’s Tale', 'Twelfth Night'): '20/80'
    }

# Define edges to be highlighted in black (unchanged logic)
def define_black_edges():
    return {
        ('Macbeth', 'A Midsummer Night’s Dream'): '1/99',
        ('Othello', 'A Midsummer Night’s Dream'): '5/95',
    }

# Calculate node positions (unchanged)
def calculate_positions(layer, x_offset):
    y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
    return [(x_offset, y) for y in y_positions]

# Create and visualize the neural network graph (unchanged logic)
def visualize_nn():
    layers = define_layers()
    colors = assign_colors()
    edges = define_edges()
    black_edges = define_black_edges()
    
    G = nx.DiGraph()
    pos = {}
    node_colors = []
    
    mapping = {}
    counter = 1
    for layer in layers.values():
        for node in layer:
            mapping[node] = f"{counter}. {node}"
            counter += 1
            
    for i, (layer_name, nodes) in enumerate(layers.items()):
        positions = calculate_positions(nodes, x_offset=i * 2)
        for node, position in zip(nodes, positions):
            new_node = mapping[node]
            G.add_node(new_node, layer=layer_name)
            pos[new_node] = position
            node_colors.append(colors.get(node, 'lightgray'))
    
    edge_colors = []
    for (source, target), weight in edges.items():
        if source in mapping and target in mapping:
            new_source = mapping[source]
            new_target = mapping[target]
            G.add_edge(new_source, new_target, weight=weight)
            edge_colors.append('black' if (source, target) in black_edges else 'lightgrey')
    
    plt.figure(figsize=(12, 8))
    edges_labels = {(u, v): d["weight"] for u, v, d in G.edges(data=True)}
    
    nx.draw(
        G, pos, with_labels=True, node_color=node_colors, edge_color=edge_colors,
        node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
    )
    nx.draw_networkx_edge_labels(G, pos, edge_labels=edges_labels, font_size=8)
    plt.title("OPRAH™: Pericentral - Shakespeare Edition. Grok-3", fontsize=18)
    plt.show()

visualize_nn()

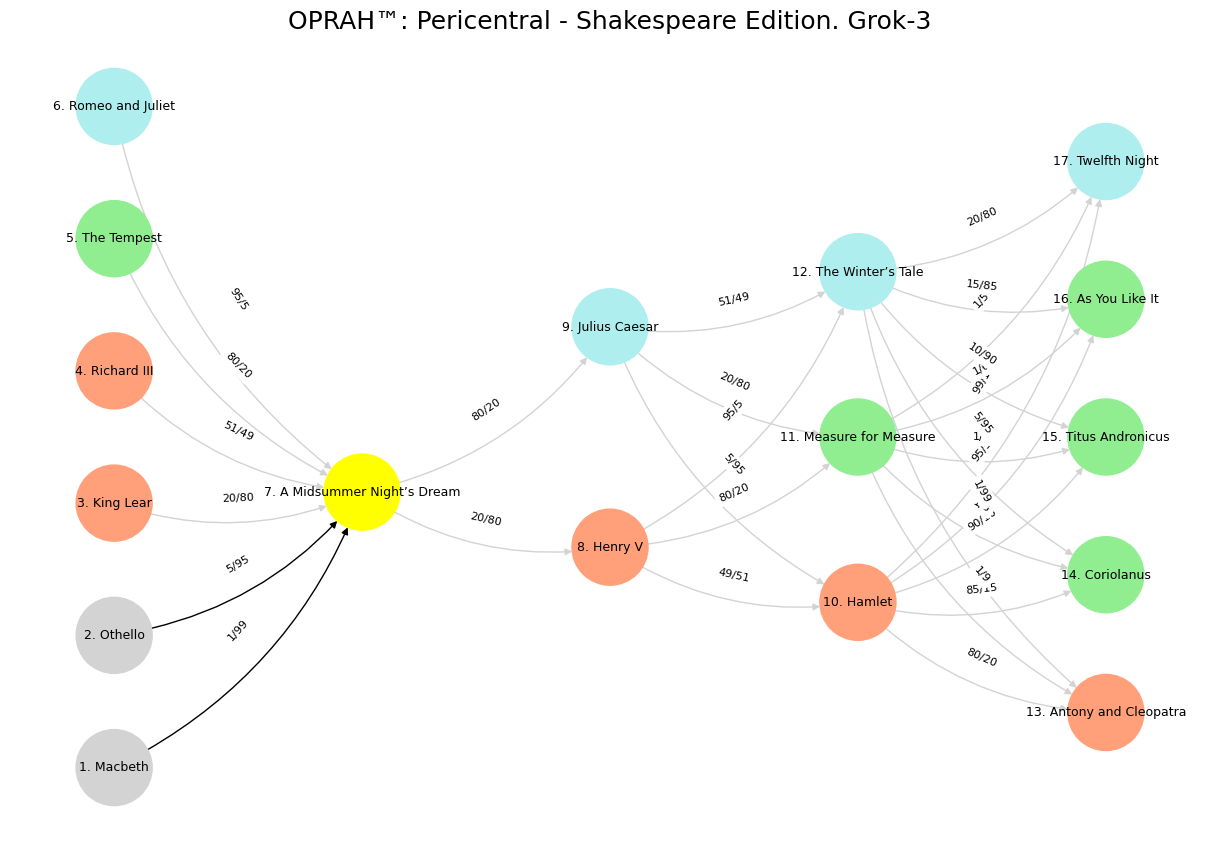
Fig. 13 Fractal Scaling. So we have CG-BEST cosmogeology, biology, ecology, symbiotology, teleology. This maps onto tragedy, history, epic, drama, and comedy. It works because of thermodynamics, nature, battle, identity, and errors. Our bequest, as understood through the lenses of cosmology, geology, biology, ecology, symbiotology, and teleology, is a tapestry woven from the threads of time, interdependence, and purpose. Cosmology reveals that we are stardust, born from the remnants of ancient supernovae, destined to return to the cosmic expanse. Geology reminds us of the Earth’s enduring resilience, its layers a testament to the slow, transformative power of time. Biology underscores our shared ancestry with all life, a reminder that we are but one thread in the intricate web of existence. Ecology teaches us the delicate balance of ecosystems, where every organism, no matter how small, plays a vital role. Symbiotology reveals the profound interconnectedness of life, where cooperation and mutualism are as essential as competition. Finally, teleology invites us to ponder our purpose—not as isolated beings, but as stewards of a legacy that transcends generations. Our bequest, then, is not merely what we leave behind, but how we honor the interconnectedness of all things, striving to preserve the balance and beauty of the world for those who will inherit it. In this, we find our true purpose: to be both guardians and participants in the grand, unfolding story of the universe.