Apollo & Dionysus#
The notes explore Robert Sapolsky’s discussion on chaos and reductionism. They argue that the role of chance makes strict reductionism impossible. Identical twins, for instance, have mitochondrial distributions that differ due to stochastic interactions, leading to unpredictability in biological systems. Reductionist frameworks break down in chaotic systems, where deterministic rules do not lead to straightforward outcomes.
Chaotic systems resemble clouds rather than clocks. Non-linear and non-additive systems cannot be pieced together in a simple manner to reconstruct their behavior. This is a challenge to reductionism.
A deterministic system that is periodic behaves predictably, whereas a deterministic but aperiodic system requires step-by-step computation for each state, making long-term predictability impossible. A truly non-deterministic system has no rules governing transitions from one state to the next.
A waterwheel analogy illustrates chaotic behavior: a system that appears structured at first can behave unpredictably when an external force disrupts its equilibrium. This leads to chaotic patterns where no periodicity exists, and patterns never repeat.
Living systems function through variability rather than order. Attempts to study them using reductionist methods obscure their complexity. Variability, rather than being noise, is an inherent feature of complex systems. Reductionism fails in biological contexts because systems such as the brain rely on distributed, non-reductive processes.
The idea of “grandmother neurons,” once thought to correspond to a single cognitive factor, fails in reality. Neurons do not work in strict isolation but as part of complex, interwoven networks.
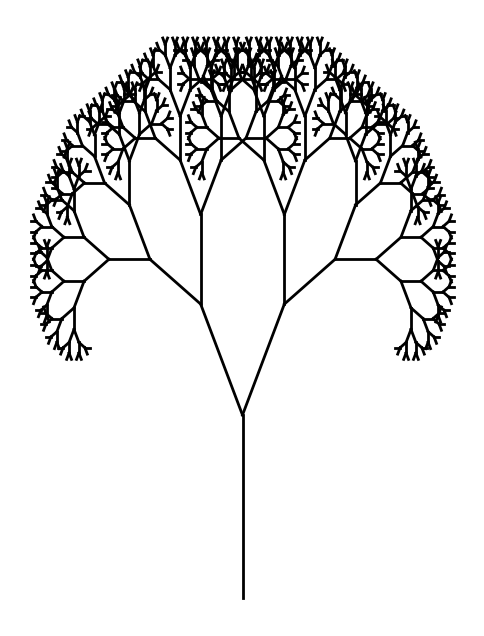
Bifurcating systems appear in nature across different scales: neurons, river deltas, bronchial trees, and circulatory networks all share similar branching structures. However, genes cannot encode such complexity through direct pointwise instruction, challenging the reductionist notion of a genetic blueprint.
Chaos systems are not reducible to a single attractor but exhibit continuous oscillation within a strange attractor, never settling into a fixed point. This reinforces the notion that complex systems resist definitive answers.
The butterfly effect is intrinsic to such systems. Tiny differences at initial conditions propagate into vastly different outcomes. Thus, variability is not an error to be removed but a fundamental property of nature.
Fractals exemplify scale-free complexity, encoding infinite complexity within finite structures. This is central to understanding chaotic systems. Fractals repeat at every scale, demonstrating the importance of self-similarity in nature.
Code to Reproduce Key Concepts
Wisdom (Streets, Earth-Bequest)
Vigilance (Owl, Trunk-Resources)
Noise-Capital (Molecule, Faustian) vs. Sigma-Talent (Epitope, Islam)
Distributed: Self (Helmet, Takaful), Negotiable (Shield, Sharakah), Nonself (Spear, Darabah)
Illusion (Lyre, Ukhuwah)
— Dionysus is filtered through Athena!
1. Bifurcating Systems (Branching Structures)
This code visualizes a simple recursive branching tree, mimicking natural bifurcating systems. From a CG-BEST fractal perspective, the notions of genius, entrepreneur, and patent are unnatural. It’s clear that in a massive combinatorial agentic-space-time, no one deserve an outsize reward from “being the first to discover”, whereupon inumerable fractal micro-decisions are the true operational means to the edifices of mankind
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
def draw_branch(x, y, angle, depth, length, ax):
if depth == 0:
return
x_end = x + length * np.cos(angle)
y_end = y + length * np.sin(angle)
ax.plot([x, x_end], [y, y_end], 'k-', lw=2)
new_length = length * 0.7
draw_branch(x_end, y_end, angle - np.pi/6, depth - 1, new_length, ax)
draw_branch(x_end, y_end, angle + np.pi/6, depth - 1, new_length, ax)
fig, ax = plt.subplots(figsize=(6, 8))
ax.set_xticks([])
ax.set_yticks([])
ax.set_frame_on(False)
draw_branch(0, -1, np.pi/2, 10, 1, ax)
plt.show()
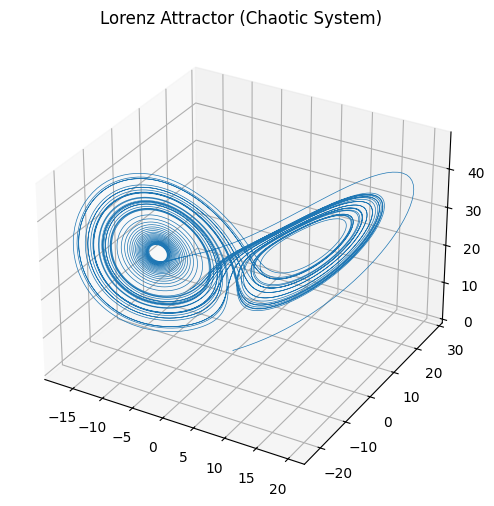
2. Strange Attractor (Chaotic System)
This code simulates a simple chaotic attractor using the Lorenz system.
#
Show code cell source
from scipy.integrate import solve_ivp
import numpy as np
import matplotlib.pyplot as plt
def lorenz(t, state, sigma=10, beta=8/3, rho=28):
x, y, z = state
dxdt = sigma * (y - x)
dydt = x * (rho - z) - y
dzdt = x * y - beta * z
return [dxdt, dydt, dzdt]
t_span = (0, 50)
initial_state = [0.1, 0.0, 0.0]
t_eval = np.linspace(t_span[0], t_span[1], 10000)
sol = solve_ivp(lorenz, t_span, initial_state, t_eval=t_eval)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
ax.plot(sol.y[0], sol.y[1], sol.y[2], lw=0.5)
ax.set_title("Lorenz Attractor (Chaotic System)")
plt.show()
3. Fractal Structure (Self-Similarity)
A visualization of the famous Mandelbrot fractal, representing infinite complexity at all scales.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
def mandelbrot(c, max_iter=100):
z = c
for n in range(max_iter):
if abs(z) > 2:
return n
z = z*z + c
return max_iter
xmin, xmax, ymin, ymax = -2.0, 1.0, -1.5, 1.5
width, height = 1000, 1000
x = np.linspace(xmin, xmax, width)
y = np.linspace(ymin, ymax, height)
mandelbrot_set = np.zeros((width, height))
for i in range(width):
for j in range(height):
mandelbrot_set[i, j] = mandelbrot(complex(x[i], y[j]))
plt.figure(figsize=(8, 8))
plt.imshow(mandelbrot_set.T, extent=[xmin, xmax, ymin, ymax], cmap="inferno")
plt.title("Mandelbrot Set (Fractal Structure)")
plt.colorbar()
plt.show()
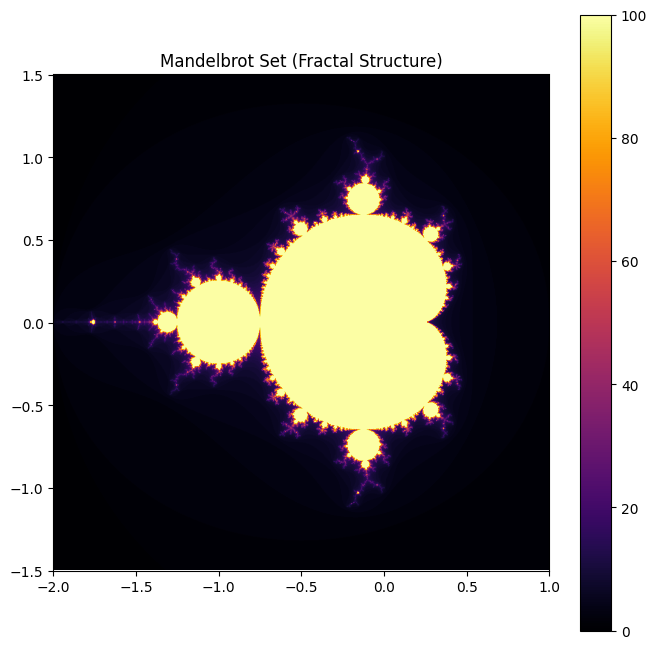

Fig. 9 Immitation. This is what distinguishes humans (really? self-similar is all fractal). We reproduce language, culture, music, behaviors, weapons of extraordinarily complex nature. A ritualization of these processes stablizes its elements and creates stability and uniformity, as well as opportunities for conflict and negotiation. These codes illustrate the key points made in Sapolsky’s discussion: the limits of reductionism, the role of chaos in biological systems, and the fundamental nature of self-similarity in complex structures.#

