Freedom in Fetters#
The Immune System as an Equilibrial Intelligence: Non-Self, Mismatch-Repair, and the Self as Adversarial, Transactional, and Cooperative
The immune system operates as a dynamic intelligence, balancing adversarial, transactional, and cooperative equilibria to maintain organismal integrity. With its ability to navigate an infinite combinatorial search space of antigens, it exemplifies an evolved form of intelligence that anticipates and responds to perturbations in a dynamic ecosystem. The interplay between self and non-self, the mechanisms of mismatch repair, and the adaptive strategies of immune selection reveal a model of intelligence based on trial-and-error reconfiguration rather than static determinism.

Fig. 29 The Next Time Your Horse is Behaving Well, Sell it. The numbers in private equity don’t add up because its very much like a betting in a horse race. Too many entrants and exits for anyone to have a reliable dataset with which to estimate odds for any horse-jokey vs. the others for quinella, trifecta, superfecta#
Non-Self as the Primordial Adversary#
The foundational adversarial equilibrium in immunity is the distinction between self and non-self, a principle articulated through the major histocompatibility complex (MHC). The immune system does not possess an innate blueprint of all potential pathogens; instead, it continuously learns through exposure. Non-self entities, such as bacterial peptidoglycans or viral nucleic acids, trigger pattern recognition receptors (PRRs) that initiate immune responses. This adversarial stance is reminiscent of game-theoretic strategies in competitive environments, where the immune system must differentiate friend from foe while minimizing collateral damage.
The concept of non-self extends beyond pathogens to aberrant self-cells, such as cancerous mutations that evade immune detection. Here, the principle of mismatch-repair emerges—a safeguard against genomic instability and protein misfolding. The immune system thus functions not only as an external sentinel but also as an internal regulator, policing deviations from cellular norms.
Mismatch-Repair as Transactional Learning#
Mismatch-repair embodies a transactional equilibrium wherein errors in DNA replication or protein synthesis are corrected through iterative proofreading. This aligns with the broader logic of trial-and-error learning seen in machine learning algorithms, wherein small perturbations inform subsequent corrections. In the immune context, this manifests in the affinity maturation of B cells, where somatic hypermutation allows for incremental refinements in antigen recognition.
Similarly, T-cell selection in the thymus follows a dual-stage process:
Positive selection ensures recognition of self-MHC molecules, preventing complete immunological blindness.
Negative selection eliminates overly self-reactive clones to prevent autoimmunity.
This transactional interplay between selection pressures ensures immune robustness while mitigating excessive aggression against host tissues.
Self as Adversarial: Autoimmunity and Immunoregulation#
The self can also be adversarial when immune checkpoints fail, leading to autoimmunity. Regulatory T cells (Tregs) mediate a cooperative equilibrium that prevents the immune system from attacking the host. Without Treg-mediated suppression, inflammatory cascades can spiral into pathological states, as seen in conditions such as rheumatoid arthritis or multiple sclerosis.
Conversely, checkpoint inhibitors like PD-1 and CTLA-4 function as strategic adversarial nodes that suppress hyperactive immune responses. This highlights a critical insight: adversarial mechanisms are not exclusively destructive; they are essential for refining and calibrating equilibria. The immune system, much like an intelligent computational network, employs adversarial testing to reinforce robustness.
Cooperative Equilibria in Immunity#
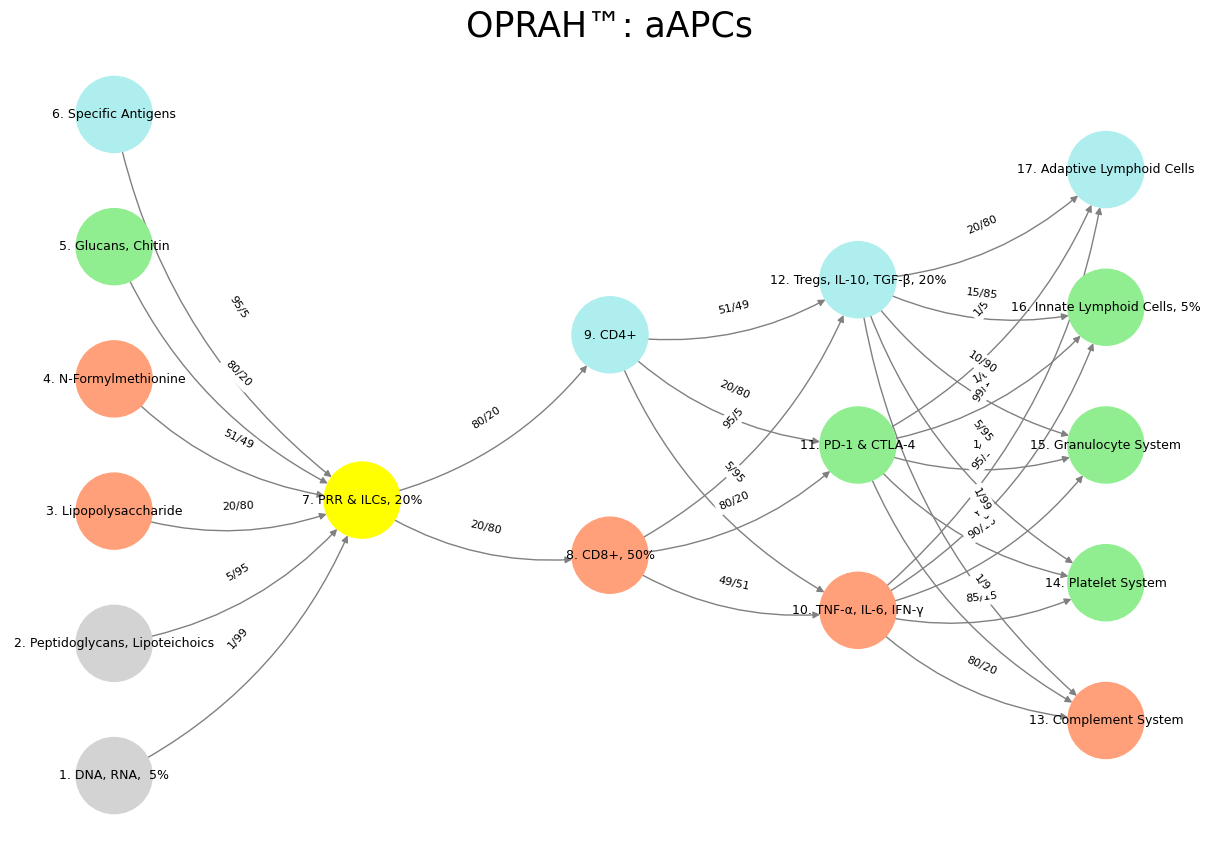
Cooperation emerges at multiple levels of immune function. Innate lymphoid cells (ILCs) and antigen-presenting cells (APCs) act as intermediaries between innate and adaptive immunity, ensuring synchronized responses. The cytokine milieu also exemplifies cooperative signaling, where pro-inflammatory (TNF-α, IL-6, IFN-γ) and anti-inflammatory (IL-10, TGF-β) factors must be dynamically balanced.
Furthermore, the complement system represents a cooperative, networked intelligence that enhances pathogen clearance through cascades of proteolytic activation. Platelets, traditionally seen in hemostasis, also engage in immune cooperation by modulating leukocyte recruitment and inflammatory signaling.
The Immune System as a Computational Model#
When mapped onto a computational neural network, the immune system exhibits features akin to artificial intelligence architectures:
Input Layer (Suis): Recognition of molecular patterns (DNA, RNA, lipopolysaccharides).
Compression Layer (Voir): PRRs and innate cells filter relevant information.
Hidden Layers (Choisis & Deviens): T-cell selection, cytokine signaling, and immune modulation.
Output Layer (M’élève): Effector responses via complement activation, granulocyte mobilization, and platelet engagement.
This structure aligns with a broader framework of biological intelligence, where trial-and-error refinement enables anticipatory adaptation to an ever-changing antigenic landscape. The dynamic weights of immune interactions—captured through cytokine gradients, cellular cross-talk, and epigenetic modifications—further underscore the immune system’s computational depth.
Conclusion: Immune Intelligence as a Model for Strategic Equilibria#
The immune system exemplifies a refined balance of adversarial, transactional, and cooperative equilibria. By engaging in a near-infinite combinatorial search of antigens, it mirrors the principles of evolutionary intelligence, where fitness is determined by the ability to navigate an uncertain and dynamic environment. Just as game theory describes strategic interactions in economic and social contexts, the immune system operates as a biological manifestation of these principles, ensuring organismal survival through sophisticated pattern recognition and adaptive recalibration. This self-organizing intelligence, deeply embedded in nature, offers profound insights into artificial intelligence, machine learning, and the broader study of strategic equilibria across disciplines.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
# Define the neural network layers
def define_layers():
return {
'Suis': ['DNA, RNA, 5%', 'Peptidoglycans, Lipoteichoics', 'Lipopolysaccharide', 'N-Formylmethionine', "Glucans, Chitin", 'Specific Antigens'], # Static
'Voir': ['PRR & ILCs, 20%'],
'Choisis': ['CD8+, 50%', 'CD4+'],
'Deviens': ['TNF-α, IL-6, IFN-γ', 'PD-1 & CTLA-4', 'Tregs, IL-10, TGF-β, 20%'],
"M'èléve": ['Complement System', 'Platelet System', 'Granulocyte System', 'Innate Lymphoid Cells, 5%', 'Adaptive Lymphoid Cells']
}
# Assign colors to nodes
def assign_colors():
color_map = {
'yellow': ['PRR & ILCs, 20%'],
'paleturquoise': ['Specific Antigens', 'CD4+', 'Tregs, IL-10, TGF-β, 20%', 'Adaptive Lymphoid Cells'],
'lightgreen': ["Glucans, Chitin", 'PD-1 & CTLA-4', 'Platelet System', 'Innate Lymphoid Cells, 5%', 'Granulocyte System'],
'lightsalmon': ['Lipopolysaccharide', 'N-Formylmethionine', 'CD8+, 50%', 'TNF-α, IL-6, IFN-γ', 'Complement System'],
}
return {node: color for color, nodes in color_map.items() for node in nodes}
# Define edge weights (hardcoded for editing)
def define_edges():
return {
('DNA, RNA, 5%', 'PRR & ILCs, 20%'): '1/99',
('Peptidoglycans, Lipoteichoics', 'PRR & ILCs, 20%'): '5/95',
('Lipopolysaccharide', 'PRR & ILCs, 20%'): '20/80',
('N-Formylmethionine', 'PRR & ILCs, 20%'): '51/49',
("Glucans, Chitin", 'PRR & ILCs, 20%'): '80/20',
('Specific Antigens', 'PRR & ILCs, 20%'): '95/5',
('PRR & ILCs, 20%', 'CD8+, 50%'): '20/80',
('PRR & ILCs, 20%', 'CD4+'): '80/20',
('CD8+, 50%', 'TNF-α, IL-6, IFN-γ'): '49/51',
('CD8+, 50%', 'PD-1 & CTLA-4'): '80/20',
('CD8+, 50%', 'Tregs, IL-10, TGF-β, 20%'): '95/5',
('CD4+', 'TNF-α, IL-6, IFN-γ'): '5/95',
('CD4+', 'PD-1 & CTLA-4'): '20/80',
('CD4+', 'Tregs, IL-10, TGF-β, 20%'): '51/49',
('TNF-α, IL-6, IFN-γ', 'Complement System'): '80/20',
('TNF-α, IL-6, IFN-γ', 'Platelet System'): '85/15',
('TNF-α, IL-6, IFN-γ', 'Granulocyte System'): '90/10',
('TNF-α, IL-6, IFN-γ', 'Innate Lymphoid Cells, 5%'): '95/5',
('TNF-α, IL-6, IFN-γ', 'Adaptive Lymphoid Cells'): '99/1',
('PD-1 & CTLA-4', 'Complement System'): '1/9',
('PD-1 & CTLA-4', 'Platelet System'): '1/8',
('PD-1 & CTLA-4', 'Granulocyte System'): '1/7',
('PD-1 & CTLA-4', 'Innate Lymphoid Cells, 5%'): '1/6',
('PD-1 & CTLA-4', 'Adaptive Lymphoid Cells'): '1/5',
('Tregs, IL-10, TGF-β, 20%', 'Complement System'): '1/99',
('Tregs, IL-10, TGF-β, 20%', 'Platelet System'): '5/95',
('Tregs, IL-10, TGF-β, 20%', 'Granulocyte System'): '10/90',
('Tregs, IL-10, TGF-β, 20%', 'Innate Lymphoid Cells, 5%'): '15/85',
('Tregs, IL-10, TGF-β, 20%', 'Adaptive Lymphoid Cells'): '20/80'
}
# Calculate positions for nodes
def calculate_positions(layer, x_offset):
y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
return [(x_offset, y) for y in y_positions]
# Create and visualize the neural network graph
def visualize_nn():
layers = define_layers()
colors = assign_colors()
edges = define_edges()
G = nx.DiGraph()
pos = {}
node_colors = []
# Create mapping from original node names to numbered labels
mapping = {}
counter = 1
for layer in layers.values():
for node in layer:
mapping[node] = f"{counter}. {node}"
counter += 1
# Add nodes with new numbered labels and assign positions
for i, (layer_name, nodes) in enumerate(layers.items()):
positions = calculate_positions(nodes, x_offset=i * 2)
for node, position in zip(nodes, positions):
new_node = mapping[node]
G.add_node(new_node, layer=layer_name)
pos[new_node] = position
node_colors.append(colors.get(node, 'lightgray'))
# Add edges with updated node labels
for (source, target), weight in edges.items():
if source in mapping and target in mapping:
new_source = mapping[source]
new_target = mapping[target]
G.add_edge(new_source, new_target, weight=weight)
# Draw the graph
plt.figure(figsize=(12, 8))
edges_labels = {(u, v): d["weight"] for u, v, d in G.edges(data=True)}
nx.draw(
G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edges_labels, font_size=8)
plt.title("OPRAH™: aAPCs", fontsize=25)
plt.show()
# Run the visualization
visualize_nn()
#
Fig. 30 Musical Grammar & Prosody. From a pianist’s perspective, the left hand serves as the foundational architect, voicing the mode and defining the musical landscape—its space and grammar—while the right hand acts as the expressive wanderer, freely extending and altering these modal terrains within temporal pockets, guided by prosody and cadence. In R&B, this interplay often manifests through rich harmonic extensions like 9ths, 11ths, and 13ths, with chromatic passing chords and leading tones adding tension and color. Music’s evocative power lies in its ability to transmit information through a primal, pattern-recognizing architecture, compelling listeners to classify what they hear as either nurturing or threatening—feeding and breeding or fight and flight. This makes music a high-risk, high-reward endeavor, where success hinges on navigating the fine line between coherence and error. Similarly, pattern recognition extends to literature, as seen in Ulysses, where a character misinterprets his companion’s silence as mental composition, reflecting on the instructive pleasures of Shakespearean works used to solve life’s complexities. Both music and literature, then, are deeply rooted in the human impulse to decode and derive meaning, whether through harmonic landscapes or textual introspection. Source: Ulysses, DeepSeek & Yours Truly!#

