Revolution#
+ Expand
- What makes for a suitable problem for AI (Demis Hassabis, Nobel Lecture)?
- Space: Massive combinatorial search space
- Function: Clear objective function (metric) to optimize against
- Time: Either lots of data and/or an accurate and efficient simulator
- Guess what else fits the bill (Yours truly, amateur philosopher)?
- Space
- Intestines/villi
- Lungs/bronchioles
- Capillary trees
- Network of lymphatics
- Dendrites in neurons
- Tree branches
- Function
- Energy
- Aerobic respiration
- Delivery to "last mile" (minimize distance)
- Response time (minimize)
- Information
- Exposure to sunlight for photosynthesis
- Time
- Nourishment
- Gaseous exchange
- Oxygen & Nutrients (Carbon dioxide & "Waste")
- Surveillance for antigens
- Coherence of functions
- Water and nutrients from soil
The nervous system and the immune system are both sophisticated information-processing architectures, but they operate under distinct paradigms of intelligence. If we take Demis Hassabis’ criteria for AI-suitable problems—combinatorial search space, optimization through an objective function, and reliance on either massive datasets or efficient simulation—and apply them to biological intelligence, we must first establish whether intelligence itself is best defined in these terms. When mapped onto a neural network framework, the immune system appears to meet these criteria in ways that the nervous system does not, raising the provocative question of whether the immune system is, in some sense, more intelligent than the brain.
The biology of ILCs also extends beyond classical immunology to metabolic homeostasis, tissue remodeling, and
dialogwith the nervous system
– Vivier et al
At its core, the nervous system functions through structured electrochemical signaling with a relatively fixed anatomical layout. Information processing relies on synaptic transmission, neural plasticity, and hierarchical control. The brain’s architecture allows for rapid decision-making, abstraction, and symbolic reasoning, which gives it the capacity for higher-order cognition. However, this structured nature also introduces a fundamental rigidity: neural circuits, while capable of learning and adaptation, are constrained by their physical wiring. The nervous system refines itself primarily through Hebbian learning, adjusting weights based on reinforcement and feedback but rarely undergoing fundamental rewiring at the structural level once development is complete.

In contrast, the immune system embodies a far more decentralized and stochastic intelligence. Its adaptability is driven not by fixed circuitry but by a dynamic, self-modifying system of antigen recognition, clonal selection, and genetic recombination. It continuously generates novel responses to previously unseen threats through hypermutation and somatic recombination, effectively searching an expansive combinatorial space. The immune system is not limited by preordained neural pathways; instead, it operates through a generative process that allows it to respond to perturbations in real-time without requiring pre-existing representations of threats. This aligns strikingly with Heraclitus’ principle that one never steps into the same river twice—whereas the brain often reuses prior experiences to make decisions, the immune system assumes that the environment is perpetually changing and thus prioritizes novel solutions over entrenched responses.
From an optimization perspective, the nervous system and immune system pursue distinct strategies. The nervous system optimizes for coherence and continuity, refining representations of the world through an iterative process of prediction and error correction. It relies on gradient-based learning, slowly sculpting itself through experiences and reinforcement loops. The immune system, on the other hand, engages in an adversarial search process with evolutionary dynamics at its core. Rather than a singular optimization function, it employs a distributed, multi-agent framework in which individual cells act as independent search nodes, each capable of mutating and recombining to increase the overall diversity of the response. This results in a system that is less deterministic than neural processing but more resilient to novel perturbations.
The starkest divergence between these two paradigms lies in their handling of uncertainty. The nervous system attempts to minimize uncertainty by generating internal models that predict the world as accurately as possible. It refines its priors, filters sensory noise, and optimizes for efficiency in signal transmission. The immune system, by contrast, thrives in uncertainty—it expects unpredictability and actively generates stochastic diversity as a defensive mechanism. Its intelligence is distributed rather than hierarchical, with no central processor orchestrating responses. Each immune cell independently contributes to the overall fitness of the system, akin to an evolutionary algorithm exploring a vast solution space. In this sense, the immune system appears to possess a deeper, more intrinsic appreciation of stochasticity than the brain does.
When we consider intelligence as a function of adaptability and combinatorial search, the immune system emerges as a model that better aligns with Hassabis’ AI criteria. It continuously updates its parameters, introduces stochastic disturbances, and never steps into the same river twice. In contrast, the nervous system optimizes for stability and coherence, often at the expense of adaptability. If we define intelligence not as static optimization but as the ability to explore vast, uncertain spaces and generate novel solutions, then the immune system may indeed surpass the nervous system in this regard. However, this does not diminish the brain’s role in higher-order reasoning; rather, it suggests that intelligence itself may be more multifaceted than traditionally conceived.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
# Define the neural network layers
def define_layers():
return {
'Suis': ['DNA, RNA, 5%', 'Peptidoglycans, Lipoteichoics', 'Lipopolysaccharide', 'N-Formylmethionine', "Glucans, Chitin", 'Specific Antigens'], # Static
'Voir': ['MHC.I/CD3-, PRR/MHC.II , 20%'],
'Choisis': ['CD8+, 50%', 'CD4+'],
'Deviens': ['TNF-α, IL-6, IFN-γ', 'PD-1 & CTLA-4', 'Tregs, IL-10, TGF-β, 20%'],
"M'èléve": ['Complement System', 'Platelet System', 'Granulocyte System', 'Innate Lymphoid Cells, 5%', 'Adaptive Lymphoid Cells']
}
# Assign colors to nodes
def assign_colors():
color_map = {
'yellow': ['MHC.I/CD3-, PRR/MHC.II , 20%'],
'paleturquoise': ['Specific Antigens', 'CD4+', 'Tregs, IL-10, TGF-β, 20%', 'Adaptive Lymphoid Cells'],
'lightgreen': ["Glucans, Chitin", 'PD-1 & CTLA-4', 'Platelet System', 'Innate Lymphoid Cells, 5%', 'Granulocyte System'],
'lightsalmon': ['Lipopolysaccharide', 'N-Formylmethionine', 'CD8+, 50%', 'TNF-α, IL-6, IFN-γ', 'Complement System'],
}
return {node: color for color, nodes in color_map.items() for node in nodes}
# Define edge weights (hardcoded for editing)
def define_edges():
return {
('DNA, RNA, 5%', 'MHC.I/CD3-, PRR/MHC.II , 20%'): '1/99',
('Peptidoglycans, Lipoteichoics', 'MHC.I/CD3-, PRR/MHC.II , 20%'): '5/95',
('Lipopolysaccharide', 'MHC.I/CD3-, PRR/MHC.II , 20%'): '20/80',
('N-Formylmethionine', 'MHC.I/CD3-, PRR/MHC.II , 20%'): '51/49',
("Glucans, Chitin", 'MHC.I/CD3-, PRR/MHC.II , 20%'): '80/20',
('Specific Antigens', 'MHC.I/CD3-, PRR/MHC.II , 20%'): '95/5',
('MHC.I/CD3-, PRR/MHC.II , 20%', 'CD8+, 50%'): '20/80',
('MHC.I/CD3-, PRR/MHC.II , 20%', 'CD4+'): '80/20',
('CD8+, 50%', 'TNF-α, IL-6, IFN-γ'): '49/51',
('CD8+, 50%', 'PD-1 & CTLA-4'): '80/20',
('CD8+, 50%', 'Tregs, IL-10, TGF-β, 20%'): '95/5',
('CD4+', 'TNF-α, IL-6, IFN-γ'): '5/95',
('CD4+', 'PD-1 & CTLA-4'): '20/80',
('CD4+', 'Tregs, IL-10, TGF-β, 20%'): '51/49',
('TNF-α, IL-6, IFN-γ', 'Complement System'): '80/20',
('TNF-α, IL-6, IFN-γ', 'Platelet System'): '85/15',
('TNF-α, IL-6, IFN-γ', 'Granulocyte System'): '90/10',
('TNF-α, IL-6, IFN-γ', 'Innate Lymphoid Cells, 5%'): '95/5',
('TNF-α, IL-6, IFN-γ', 'Adaptive Lymphoid Cells'): '99/1',
('PD-1 & CTLA-4', 'Complement System'): '1/9',
('PD-1 & CTLA-4', 'Platelet System'): '1/8',
('PD-1 & CTLA-4', 'Granulocyte System'): '1/7',
('PD-1 & CTLA-4', 'Innate Lymphoid Cells, 5%'): '1/6',
('PD-1 & CTLA-4', 'Adaptive Lymphoid Cells'): '1/5',
('Tregs, IL-10, TGF-β, 20%', 'Complement System'): '1/99',
('Tregs, IL-10, TGF-β, 20%', 'Platelet System'): '5/95',
('Tregs, IL-10, TGF-β, 20%', 'Granulocyte System'): '10/90',
('Tregs, IL-10, TGF-β, 20%', 'Innate Lymphoid Cells, 5%'): '15/85',
('Tregs, IL-10, TGF-β, 20%', 'Adaptive Lymphoid Cells'): '20/80'
}
# Calculate positions for nodes
def calculate_positions(layer, x_offset):
y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
return [(x_offset, y) for y in y_positions]
# Create and visualize the neural network graph
def visualize_nn():
layers = define_layers()
colors = assign_colors()
edges = define_edges()
G = nx.DiGraph()
pos = {}
node_colors = []
# Create mapping from original node names to numbered labels
mapping = {}
counter = 1
for layer in layers.values():
for node in layer:
mapping[node] = f"{counter}. {node}"
counter += 1
# Add nodes with new numbered labels and assign positions
for i, (layer_name, nodes) in enumerate(layers.items()):
positions = calculate_positions(nodes, x_offset=i * 2)
for node, position in zip(nodes, positions):
new_node = mapping[node]
G.add_node(new_node, layer=layer_name)
pos[new_node] = position
node_colors.append(colors.get(node, 'lightgray'))
# Add edges with updated node labels
for (source, target), weight in edges.items():
if source in mapping and target in mapping:
new_source = mapping[source]
new_target = mapping[target]
G.add_edge(new_source, new_target, weight=weight)
# Draw the graph
plt.figure(figsize=(12, 8))
edges_labels = {(u, v): d["weight"] for u, v, d in G.edges(data=True)}
nx.draw(
G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edges_labels, font_size=8)
plt.title("OPRAH™: aAPCs", fontsize=25)
plt.show()
# Run the visualization
visualize_nn()
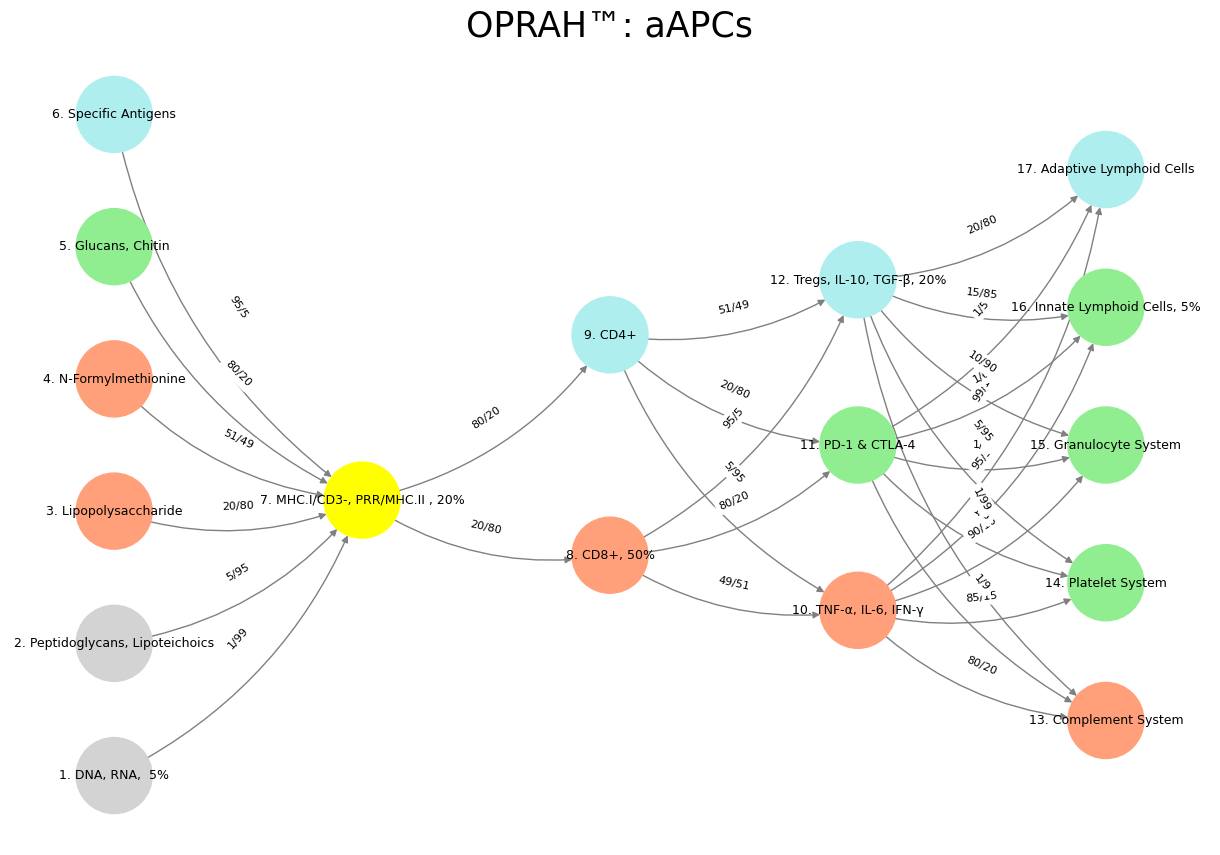

Fig. 25 Francis Bacon. He famously stated “If a man will begin with certainties, he shall end in doubts; but if he will be content to begin with doubts, he shall end in certainties.” This quote is from The Advancement of Learning (1605), where Bacon lays out his vision for empirical science and inductive reasoning. He argues that starting with unquestioned assumptions leads to instability and confusion, whereas a methodical approach that embraces doubt and inquiry leads to true knowledge. This aligns with his broader Novum Organum (1620), where he develops the Baconian method, advocating for systematic observation, experimentation, and the gradual accumulation of knowledge rather than relying on dogma or preconceived notions.#