4 Python#
Show code cell source
import pandas as pd
# Load the Stata dataset
url = "https://github.com/muzaale/forum/raw/main/esrdRisk_t02tT.dta"
data = pd.read_stata(url)
# Save the dataset as a CSV file
data.to_csv('esrdRisk_t02tT.csv', index=False)
print("CSV file saved as 'esrdRisk_t02tT.csv'")
CSV file saved as 'esrdRisk_t02tT.csv'
import pandas as pd
# Load the CSV dataset
data = pd.read_csv('./esrdRisk_t02tT.csv', low_memory=False)
# Print unique values in 'rSMGJcEdF_d'
print(data['rSMGJcEdF_d'].unique())
['Censored' 'Died' 'ESRD']
import pandas as pd
# Load the CSV dataset
data = pd.read_csv('./esrdRisk_t02tT.csv', low_memory=False)
# Display basic information about the dataset
print("Dataset information:")
print(data.info())
Show code cell output
Dataset information:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 113657 entries, 0 to 113656
Data columns (total 40 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 pers_id 113657 non-null int64
1 don_id 96217 non-null object
2 don_yearcat 96217 non-null object
3 don_age 113657 non-null int64
4 don_agecat 113657 non-null object
5 don_female 113657 non-null object
6 don_race_ethn 113599 non-null object
7 don_educat 72127 non-null object
8 don_hyperten 63736 non-null object
9 don_smoke 59119 non-null object
10 don_bmi 86983 non-null float64
11 don_bmicat 86983 non-null object
12 don_bp_preop_syst 82898 non-null float64
13 don_sbpcat 82898 non-null object
14 don_bp_preop_diast 82857 non-null float64
15 don_dbpcat 82857 non-null object
16 don_egfr 90651 non-null float64
17 don_egfrcat 90651 non-null object
18 creat 90687 non-null float64
19 don_related 96042 non-null object
20 n2e_d 113657 non-null object
21 n2e_t 113657 non-null float64
22 donor 113657 non-null object
23 healthy 17440 non-null object
24 acr 112687 non-null float64
25 case 113657 non-null int64
26 id 113657 non-null float64
27 rSMGJcEdF_d 113657 non-null object
28 rSMGJcEdF_t0 113657 non-null object
29 rSMGJcEdF_tT 113657 non-null object
30 rSMGJcEdF_t 113657 non-null float64
31 rSMGJcEdF_x 113657 non-null object
32 age_t0 113657 non-null int64
33 age_tT 113657 non-null float64
34 female 113657 non-null int64
35 race 113599 non-null float64
36 _st 113657 non-null int64
37 _d 113657 non-null int64
38 _t 113657 non-null float64
39 _t0 113657 non-null int64
dtypes: float64(12), int64(8), object(20)
memory usage: 34.7+ MB
None
# Display the first few rows of the dataset to understand its structure
print("\nFirst few rows of the dataset:")
print(data.head())
Show code cell output
First few rows of the dataset:
pers_id don_id don_yearcat don_age don_agecat don_female don_race_ethn \
0 5005738 AAEN566 1998-2001 44 40-49 Female White/Other
1 4973528 ZIF796 2002-2005 47 40-49 Female White/Other
2 4961779 ZFV631 2002-2005 38 18-39 Female Hispanic
3 4961603 ZFN933 2006-2009 38 18-39 Male Hispanic
4 4949318 ZCU948 1998-2001 18 18-39 Female White/Other
don_educat don_hyperten don_smoke ... rSMGJcEdF_t rSMGJcEdF_x age_t0 \
0 NaN No History Smoker ... 11.192334 rSM 44
1 <HighSchool NaN NoHistory ... 6.743327 rSM 47
2 <HighSchool No History NoHistory ... 6.086242 rSM 38
3 <HighSchool No History NoHistory ... 5.607119 rSM 38
4 NaN No History NoHistory ... 11.731690 rSM 18
age_tT female race _st _d _t _t0
0 55.192333 1 1.0 1 0 11.192334 0
1 53.743330 1 1.0 1 0 6.743327 0
2 44.086243 1 3.0 1 0 6.086242 0
3 43.607117 0 3.0 1 0 5.607119 0
4 29.731690 1 1.0 1 0 11.731690 0
[5 rows x 40 columns]
# Total number of observations and variables
num_observations = data.shape[0]
num_variables = data.shape[1]
print(f"\nTotal number of observations: {num_observations}")
print(f"Total number of variables: {num_variables}")
Total number of observations: 113657
Total number of variables: 40
# Display the outcome of interest and its format
print("\nOutcome of interest (rSMGJcEdF_d) and its format:")
print(data['rSMGJcEdF_d'].value_counts(dropna=False))
Outcome of interest (rSMGJcEdF_d) and its format:
rSMGJcEdF_d
Censored 108448
Died 4939
ESRD 270
Name: count, dtype: int64
Show code cell source
# Display the start time (rSMGJcEdF_t0) and end time (rSMGJcEdF_tT) for survival analysis
print("\nStart time (rSMGJcEdF_t0):")
print(data['rSMGJcEdF_t0'].head())
print("\nEnd time (rSMGJcEdF_tT):")
print(data['rSMGJcEdF_tT'].head())
Show code cell output
Start time (rSMGJcEdF_t0):
0 2000-09-20
1 2005-03-03
2 2005-10-29
3 2006-04-22
4 2000-03-07
Name: rSMGJcEdF_t0, dtype: object
End time (rSMGJcEdF_tT):
0 2014-07-31
1 2014-07-31
2 2014-07-31
3 2014-07-31
4 2014-07-31
Name: rSMGJcEdF_tT, dtype: object
Show code cell source
import pandas as pd
import numpy as np
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
# Load the CSV dataset
data = pd.read_csv('./esrdRisk_t02tT.csv', low_memory=False)
# Convert date columns to datetime
data['rSMGJcEdF_t0'] = pd.to_datetime(data['rSMGJcEdF_t0'])
data['rSMGJcEdF_tT'] = pd.to_datetime(data['rSMGJcEdF_tT'])
# Calculate follow-up time in years
data['duration'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Map non-numeric values to numeric
value_mapping = {'Censored': 0, 'Died': 0, 'ESRD': 1}
data['rSMGJcEdF_d'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)
# Apply the same date restrictions as in Stata
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_d'] = 0
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_tT'] = pd.to_datetime('2011-12-31')
data.loc[(data['rSMGJcEdF_t0'] < '1994-01-01') & (data['rSMGJcEdF_tT'] > '1994-01-01'), 'rSMGJcEdF_t0'] = pd.to_datetime('1994-01-01')
# Recalculate duration after date adjustments
data['duration'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Create the 'event' column (rSMGJcEdF_d == 1 indicates an event)
data['event'] = data['rSMGJcEdF_d'] == 1
# Filter relevant columns and drop rows with missing values
data = data[['duration', 'event', 'donor']].dropna()
# Display the processed data
print("\nProcessed data:")
print(data.info())
print(data.head())
Show code cell output
Processed data:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 113657 entries, 0 to 113656
Data columns (total 3 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 duration 113657 non-null float64
1 event 113657 non-null bool
2 donor 113657 non-null object
dtypes: bool(1), float64(1), object(1)
memory usage: 1.8+ MB
None
duration event donor
0 11.277207 False Donor
1 6.828200 False Donor
2 6.171116 False Donor
3 5.691992 False Donor
4 11.816564 False Donor
/var/folders/z3/nwmg00j178vfczmb9nk9487h0000gn/T/ipykernel_48040/812990944.py:18: FutureWarning: Downcasting behavior in `replace` is deprecated and will be removed in a future version. To retain the old behavior, explicitly call `result.infer_objects(copy=False)`. To opt-in to the future behavior, set `pd.set_option('future.no_silent_downcasting', True)`
data['rSMGJcEdF_d'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)
Show code cell source
import pandas as pd
import numpy as np
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
# Load the CSV dataset
data = pd.read_csv('./esrdRisk_t02tT.csv', low_memory=False)
# Convert date columns to datetime
data['rSMGJcEdF_t0'] = pd.to_datetime(data['rSMGJcEdF_t0'])
data['rSMGJcEdF_tT'] = pd.to_datetime(data['rSMGJcEdF_tT'])
# Calculate follow-up time in years
data['duration'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Map non-numeric values to numeric
value_mapping = {'Censored': 0, 'Died': 0, 'ESRD': 1}
data['rSMGJcEdF_d'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)
# Apply the same date restrictions as in Stata
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_d'] = 0
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_tT'] = pd.to_datetime('2011-12-31')
data.loc[(data['rSMGJcEdF_t0'] < '1994-01-01') & (data['rSMGJcEdF_tT'] > '1994-01-01'), 'rSMGJcEdF_t0'] = pd.to_datetime('1994-01-01')
# Recalculate duration after date adjustments
data['duration'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Create the 'event' column (rSMGJcEdF_d == 1 indicates an event)
data['event'] = data['rSMGJcEdF_d'] == 1
# Create the 'donor' column with three categories
data['donor'] = np.where(data['don_id'].notna(), 'Living donor',
np.where(data['don_id'].isna() & (data['don_age'] <= 60), 'Healthy nondonor', 'General population'))
# Verify the donor categories
print("\nDonor categories:")
print(data['donor'].value_counts())
# Verify the event counts (ESRD)
print("\nEvent counts (ESRD):")
print(data['event'].value_counts())
# Filter relevant columns and drop rows with missing values
data = data[['duration', 'event', 'donor']].dropna()
# Ensure 'duration' and 'event' are numeric
data['duration'] = pd.to_numeric(data['duration'], errors='coerce')
data['event'] = pd.to_numeric(data['event'], errors='coerce')
# Display the processed data
print("\nProcessed data:")
print(data.info())
print(data.head())
# Fit the Kaplan-Meier estimator for each group
kmf = KaplanMeierFitter()
# Initialize the plot
plt.figure(figsize=(10, 6))
# Plot the Kaplan-Meier curves for each group
for label, group in data.groupby('donor'):
kmf.fit(group['duration'], event_observed=group['event'], label=label)
plt.step(kmf.timeline, 10000 * (1 - kmf.survival_function_), where="post", label=label)
# Set axis limits and labels
plt.ylim(0, 40)
plt.xlim(0, 15)
plt.xlabel('Follow-up time (years)')
plt.ylabel('Cumulative incidence (per 10,000)')
plt.title('Kaplan-Meier Failure Curve')
plt.grid(True)
# Add legend
plt.legend(loc='upper left')
# Add y-axis ticks
plt.yticks(range(0, 300, 50))
plt.tight_layout()
plt.savefig('./KM_plot.png', dpi=300, bbox_inches='tight')
plt.show()
# Print cumulative incidence at 5, 12, and 15 years
for label, group in data.groupby('donor'):
kmf.fit(group['duration'], event_observed=group['event'])
print(f"\n{label}:")
for year in [5, 12, 15]:
ci = 10000 * (1 - kmf.survival_function_at_times(year).iloc[0])
print(f" {year} years: {ci:.2f} per 10,000")
Show code cell output
/var/folders/z3/nwmg00j178vfczmb9nk9487h0000gn/T/ipykernel_48040/1010938149.py:18: FutureWarning: Downcasting behavior in `replace` is deprecated and will be removed in a future version. To retain the old behavior, explicitly call `result.infer_objects(copy=False)`. To opt-in to the future behavior, set `pd.set_option('future.no_silent_downcasting', True)`
data['rSMGJcEdF_d'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)
Donor categories:
donor
Living donor 96217
Healthy nondonor 12208
General population 5232
Name: count, dtype: int64
Event counts (ESRD):
event
False 113387
True 270
Name: count, dtype: int64
Processed data:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 113657 entries, 0 to 113656
Data columns (total 3 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 duration 113657 non-null float64
1 event 113657 non-null bool
2 donor 113657 non-null object
dtypes: bool(1), float64(1), object(1)
memory usage: 1.8+ MB
None
duration event donor
0 11.277207 False Living donor
1 6.828200 False Living donor
2 6.171116 False Living donor
3 5.691992 False Living donor
4 11.816564 False Living donor
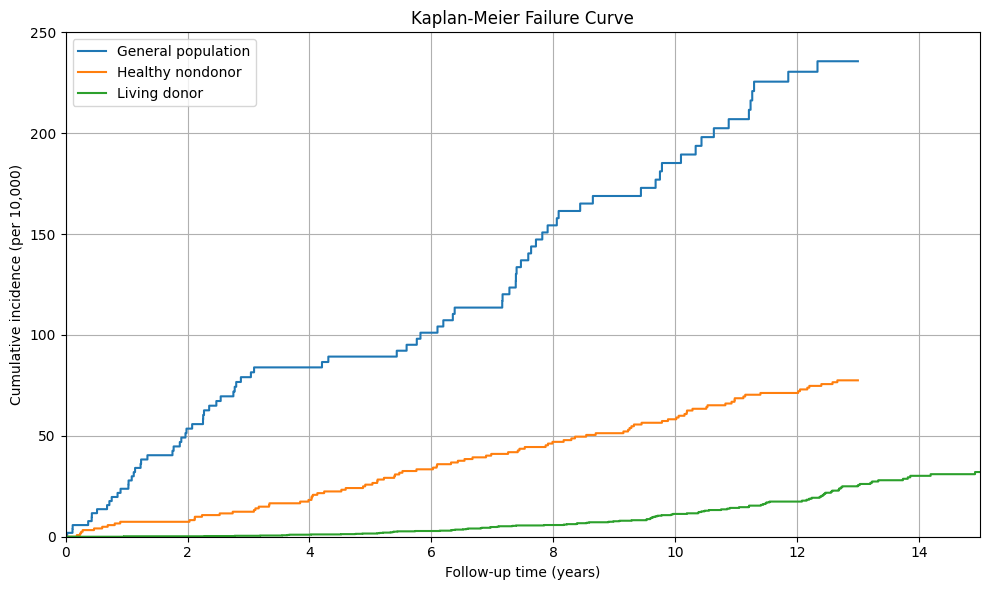
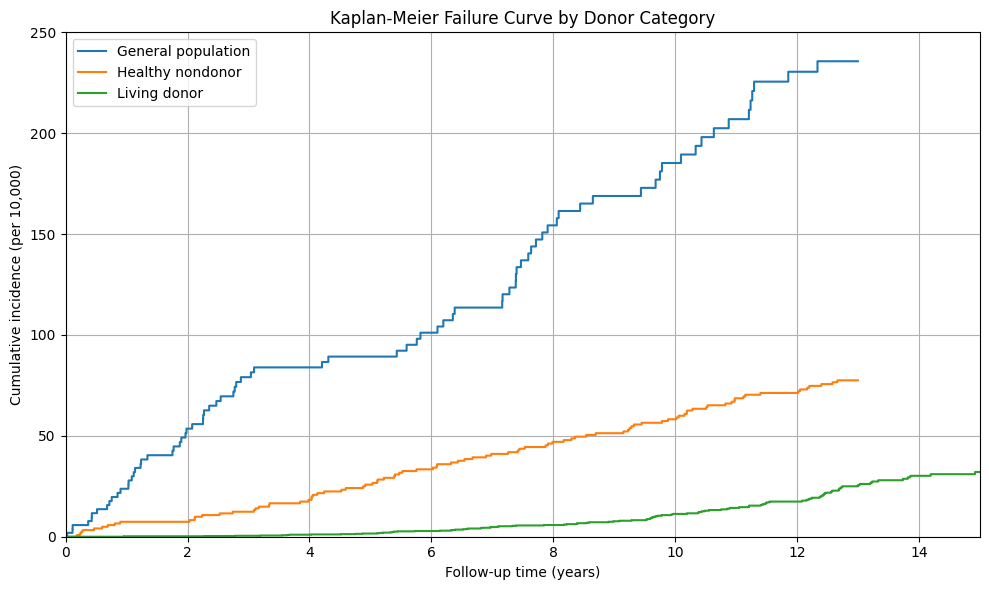
General population:
5 years: 89.28 per 10,000
12 years: 230.46 per 10,000
15 years: 235.67 per 10,000
Healthy nondonor:
5 years: 25.81 per 10,000
12 years: 71.25 per 10,000
15 years: 77.51 per 10,000
Living donor:
5 years: 1.58 per 10,000
12 years: 17.42 per 10,000
15 years: 32.06 per 10,000
Show code cell source
import pandas as pd
import numpy as np
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
# Load the CSV dataset
data = pd.read_csv('./esrdRisk_t02tT.csv', low_memory=False)
# Convert date columns to datetime
data['rSMGJcEdF_t0'] = pd.to_datetime(data['rSMGJcEdF_t0'])
data['rSMGJcEdF_tT'] = pd.to_datetime(data['rSMGJcEdF_tT'])
# Calculate follow-up time in years
data['time_to_failure'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Map non-numeric values to numeric for event_observed
value_mapping = {'Censored': 0, 'Died': 0, 'ESRD': 1}
data['status'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)
# Apply the same date restrictions as in Stata
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_d'] = 0
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_tT'] = pd.to_datetime('2011-12-31')
data.loc[(data['rSMGJcEdF_t0'] < '1994-01-01') & (data['rSMGJcEdF_tT'] > '1994-01-01'), 'rSMGJcEdF_t0'] = pd.to_datetime('1994-01-01')
# Recalculate duration after date adjustments
data['time_to_failure'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Filter relevant columns and drop rows with missing values
data = data[['time_to_failure', 'status']].dropna()
# Instantiate the KaplanMeierFitter
kmf = KaplanMeierFitter()
# Fit the data into the model
kmf.fit(data['time_to_failure'], event_observed=data['status'])
# Get the survival function
survival_function = kmf.survival_function_
# Compute 1 minus the survival function
complement_survival_function = 1 - survival_function
# Plot the complement of the Kaplan-Meier survival curve
plt.figure(figsize=(10, 6))
plt.plot(complement_survival_function, label='1 - Kaplan-Meier Estimate')
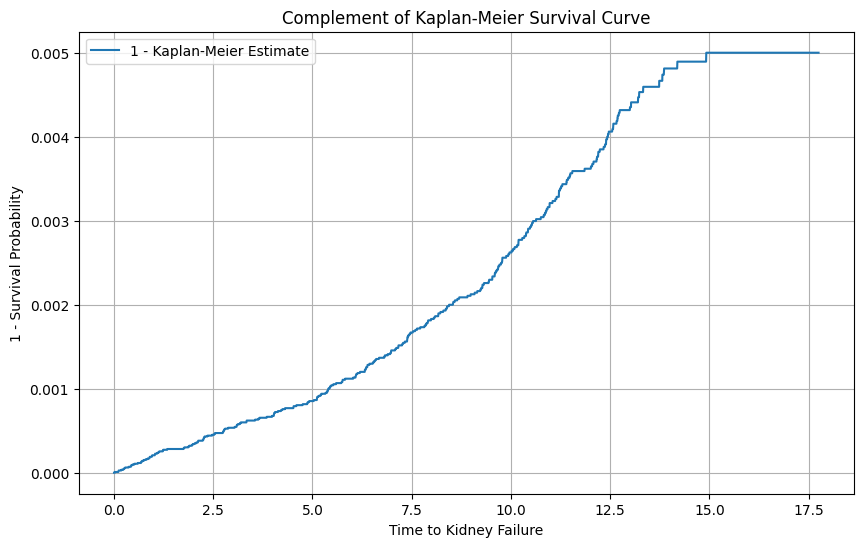
plt.title('Complement of Kaplan-Meier Survival Curve')
plt.xlabel('Time to Kidney Failure')
plt.ylabel('1 - Survival Probability')
plt.legend()
plt.grid(True)
plt.savefig('1_min_KM.png')
plt.show()
# Check if 'don_id' and 'don_age' columns exist
if 'don_id' in data.columns and 'don_age' in data.columns:
# Create the 'donor' column with three categories
data['donor'] = np.where(data['don_id'].notna(), 'Living donor',
np.where(data['don_id'].isna() & (data['don_age'] <= 60), 'Healthy nondonor', 'General population'))
# Verify the donor categories
print("\nDonor categories:")
print(data['donor'].value_counts())
# Verify the event counts (ESRD)
print("\nEvent counts (ESRD):")
print(data['event'].value_counts())
# Filter relevant columns and drop rows with missing values
data = data[['time_to_failure', 'status', 'donor']].dropna()
# Fit the Kaplan-Meier estimator for each group
kmf = KaplanMeierFitter()
# Initialize the plot
plt.figure(figsize=(10, 6))
# Plot the Kaplan-Meier curves for each group
for label, group in data.groupby('donor'):
kmf.fit(group['time_to_failure'], event_observed=group['status'], label=label)
plt.step(kmf.timeline, 10000 * (1 - kmf.survival_function_), where="post", label=label)
# Set axis limits and labels
plt.ylim(0, 40)
plt.xlim(0, 15)
plt.xlabel('Follow-up time (years)')
plt.ylabel('Cumulative incidence (per 10,000)')
plt.title('Kaplan-Meier Failure Curve')
plt.grid(True)
# Add legend
plt.legend(loc='upper left')
# Add y-axis ticks
plt.yticks(range(0, 300, 50))
plt.tight_layout()
plt.savefig('./KM_plot.png', dpi=300, bbox_inches='tight')
plt.show()
# Print cumulative incidence at 5, 12, and 15 years
for label, group in data.groupby('donor'):
kmf.fit(group['time_to_failure'], event_observed=group['status'])
print(f"\n{label}:")
for year in [5, 12, 15]:
ci = 10000 * (1 - kmf.survival_function_at_times(year).iloc[0])
print(f" {year} years: {ci:.2f} per 10,000")
else:
print("Columns 'don_id' or 'don_age' not found in the dataset.")
/var/folders/z3/nwmg00j178vfczmb9nk9487h0000gn/T/ipykernel_48040/2454471136.py:18: FutureWarning: Downcasting behavior in `replace` is deprecated and will be removed in a future version. To retain the old behavior, explicitly call `result.infer_objects(copy=False)`. To opt-in to the future behavior, set `pd.set_option('future.no_silent_downcasting', True)`
data['status'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)
Columns 'don_id' or 'don_age' not found in the dataset.
Show code cell source
import pandas as pd
import numpy as np
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
# Load the CSV dataset
data = pd.read_csv('./esrdRisk_t02tT.csv', low_memory=False)
# Convert date columns to datetime
data['rSMGJcEdF_t0'] = pd.to_datetime(data['rSMGJcEdF_t0'])
data['rSMGJcEdF_tT'] = pd.to_datetime(data['rSMGJcEdF_tT'])
# Calculate follow-up time in years
data['time_to_failure'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Map non-numeric values to numeric for event_observed
value_mapping = {'Censored': 0, 'Died': 0, 'ESRD': 1}
data['status'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)
# Apply the same date restrictions as in Stata
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_d'] = 0
data.loc[data['rSMGJcEdF_tT'] > '2011-12-31', 'rSMGJcEdF_tT'] = pd.to_datetime('2011-12-31')
data.loc[(data['rSMGJcEdF_t0'] < '1994-01-01') & (data['rSMGJcEdF_tT'] > '1994-01-01'), 'rSMGJcEdF_t0'] = pd.to_datetime('1994-01-01')
# Recalculate duration after date adjustments
data['time_to_failure'] = (data['rSMGJcEdF_tT'] - data['rSMGJcEdF_t0']).dt.days / 365.25
# Create the 'donor' column with three categories
if 'don_id' in data.columns and 'don_age' in data.columns:
data['donor'] = np.where(data['don_id'].notna(), 'Living donor',
np.where(data['don_id'].isna() & (data['don_age'] <= 60), 'Healthy nondonor', 'General population'))
# Filter relevant columns and drop rows with missing values
data = data[['time_to_failure', 'status', 'donor']].dropna()
# Fit the Kaplan-Meier estimator for each group
kmf = KaplanMeierFitter()
# Initialize the plot
plt.figure(figsize=(10, 6))
# Plot the Kaplan-Meier curves for each group
for label, group in data.groupby('donor'):
kmf.fit(group['time_to_failure'], event_observed=group['status'], label=label)
plt.step(kmf.timeline, 10000 * (1 - kmf.survival_function_), where="post", label=label)
# Set axis limits and labels
plt.ylim(0, 40)
plt.xlim(0, 15)
plt.xlabel('Follow-up time (years)')
plt.ylabel('Cumulative incidence (per 10,000)')
plt.title('Kaplan-Meier Failure Curve by Donor Category')
plt.grid(True)
# Add legend
plt.legend(loc='upper left')
# Add y-axis ticks
plt.yticks(range(0, 300, 50))
plt.tight_layout()
plt.savefig('./KM_plot_by_donor.png', dpi=300, bbox_inches='tight')
plt.show()
else:
print("Columns 'don_id' or 'don_age' not found in the dataset.")
/var/folders/z3/nwmg00j178vfczmb9nk9487h0000gn/T/ipykernel_48040/4095442099.py:18: FutureWarning: Downcasting behavior in `replace` is deprecated and will be removed in a future version. To retain the old behavior, explicitly call `result.infer_objects(copy=False)`. To opt-in to the future behavior, set `pd.set_option('future.no_silent_downcasting', True)`
data['status'] = data['rSMGJcEdF_d'].replace(value_mapping).astype(int)