Normative

The fractal embedded in this neural network is not merely a structure of nodes and edges; it is a compression of epistemology into a networked lattice, a recursive articulation of syntax, belief, and rhythm as the moving parts of cognition. This is no mere computational exercise; it is a philosophical map of transformation. The five-layered hierarchy—Suis, Voir, Choisis, Deviens, M’élève—is a teleological sequence, progressing from the static realization of self (Suis) to the elevation of self (M’élève). This architecture, in effect, mirrors the dialectic of individuation, a self-aware compression of knowledge, experience, and belief into a network that sustains its own emergent order.

Fig. 34 Theory is Good. Convergence is perhaps the most fruitful idea when comparing Business Intelligence (BI) and Artificial Intelligence (AI), as both disciplines ultimately seek the same end: extracting meaningful patterns from vast amounts of data to drive informed decision-making. BI, rooted in structured data analysis and human-guided interpretation, refines historical trends into actionable insights, whereas AI, with its machine learning algorithms and adaptive neural networks, autonomously discovers hidden relationships and predicts future outcomes. Despite their differing origins—BI arising from statistical rigor and human oversight, AI evolving through probabilistic modeling and self-optimization—their convergence leads to a singular outcome: efficiency. Just as military strategy, economic competition, and biological evolution independently refine paths toward dominance, so too do BI and AI arrive at the same pinnacle of intelligence through distinct methodologies. Victory, whether in the marketplace or on the battlefield, always bears the same hue—one of optimized decision-making, where noise is silenced, and clarity prevails. Language is about conveying meaning (Hinton). And meaning is emotions (Yours truly). These feelings are encoded in the 17 nodes of our neural network below and language and symbols attempt to capture these nodes and emotions, as well as the cadences (the edges connecting them). So the dismissiveness of Hinton with regard to Chomsky is unnecessary and perhaps harmful.

At its core, the model operates within a tightly controlled dynamism: syntax feeds into belief, punctuation into rhythm, adversarial interactions into victory. What emerges is a delicate interplay between structure and agency, a game of constraint and transcendence. The edge weights serve as probabilistic signals, hinting at the degree of influence one node exerts over another. Syntax does not hold equal weight in all contexts; its relationship to rhythm, for example, is overwhelmingly dominant at 80/20, suggesting that structure can be subsumed into flow but not erased. Likewise, adversarial engagement tilts overwhelmingly towards victory (80/20), a stark recognition of the asymmetric returns of conflict.

The neural network here is not static—it is an evolving ecosystem, where the flows between layers dictate an emergent understanding of knowledge and action. The transition from Choisis to Deviens is particularly interesting: punctuation and belief become the conduits to transactional and adversarial pathways. This suggests a fundamental truth: choice is not merely an assertion of will but a structural transformation, a shift in equilibrium that redirects meaning into new configurations.

Colors in the network are not arbitrary; they map onto distinct cognitive and structural functions. Syntax, coded in yellow, is fundamental—it is the rule-set, the grammar of engagement. Paleturquoise, encompassing time, belief, and rhythm, is the space of iteration, the reservoir of endurance. Lightgreen governs transactional dynamics, loyalty, and payoff, embedding the concept of sustained interaction. Lightsalmon dominates punctuation, adversariality, and victory—marking the thresholds, the moments of crisis where systems undergo rupture and reformation.

Yet, the most intriguing feature of this system is its recursive symmetry. The adversarial node, once introduced, does not dissipate but intensifies, feeding into victory, payoff, loyalty, and time itself. This suggests that once conflict enters the system, it does not exit; it transforms into its own form of stability. This is a model that understands power—not as a transient force but as an iterative function, a rhythm embedded in the very syntax of cognition.

The final rendering of the graph, titled Bacon Ain’t Shakespeare!, is an ironic nod to the ongoing debates of authorship, a recognition that while structures may guide expression, the individual mind is irreducible. It suggests that even within a rigid neural lattice, something escapes, something unaccounted for by mere notation—a Shakespearean surplus, a residue of the ineffable.

This is not merely a visualization of a neural network; it is an epistemic argument encoded in graph form. It posits that knowledge is neither linear nor hierarchical but fractal, a recursive interplay of structure and flow, constraint and liberation. It is an adversarial dance with syntax, where punctuation signals transformation, and rhythm carries the pulse of cognition itself.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# Define the neural network layers
def define_layers():
    return {
        'Suis': ['Opportunity', 'Inherited/Discovered', 'Syntax', 'Punctuation', "Rhythm", 'Time'],  # Static
        'Voir': ['Syntax.'],  
        'Choisis': ['Punctuation.', 'Belief'],  
        'Deviens': ['Adversarial', 'Transactional', 'Rhythm.'],  
        "M'èléve": ['Victory', 'Payoff', 'Loyalty', 'Time.', 'Distribution']  
    }

# Assign colors to nodes
def assign_colors():
    color_map = {
        'yellow': ['Syntax.'],  
        'paleturquoise': ['Time', 'Belief', 'Rhythm.', 'Distribution'],  
        'lightgreen': ["Rhythm", 'Transactional', 'Payoff', 'Time.', 'Loyalty'],  
        'lightsalmon': ['Syntax', 'Punctuation', 'Punctuation.', 'Adversarial', 'Victory'],
    }
    return {node: color for color, nodes in color_map.items() for node in nodes}

# Define edge weights (hardcoded for editing)
def define_edges():
    return {
        ('Opportunity', 'Syntax.'): '1/99',
        ('Inherited/Discovered', 'Syntax.'): '5/95',
        ('Syntax', 'Syntax.'): '20/80',
        ('Punctuation', 'Syntax.'): '51/49',
        ("Rhythm", 'Syntax.'): '80/20',
        ('Time', 'Syntax.'): '95/5',
        ('Syntax.', 'Punctuation.'): '20/80',
        ('Syntax.', 'Belief'): '80/20',
        ('Punctuation.', 'Adversarial'): '49/51',
        ('Punctuation.', 'Transactional'): '80/20',
        ('Punctuation.', 'Rhythm.'): '95/5',
        ('Belief', 'Adversarial'): '5/95',
        ('Belief', 'Transactional'): '20/80',
        ('Belief', 'Rhythm.'): '51/49',
        ('Adversarial', 'Victory'): '80/20',
        ('Adversarial', 'Payoff'): '85/15',
        ('Adversarial', 'Loyalty'): '90/10',
        ('Adversarial', 'Time.'): '95/5',
        ('Adversarial', 'Distribution'): '99/1',
        ('Transactional', 'Victory'): '1/9',
        ('Transactional', 'Payoff'): '1/8',
        ('Transactional', 'Loyalty'): '1/7',
        ('Transactional', 'Time.'): '1/6',
        ('Transactional', 'Distribution'): '1/5',
        ('Rhythm.', 'Victory'): '1/99',
        ('Rhythm.', 'Payoff'): '5/95',
        ('Rhythm.', 'Loyalty'): '10/90',
        ('Rhythm.', 'Time.'): '15/85',
        ('Rhythm.', 'Distribution'): '20/80'
    }

# Calculate positions for nodes
def calculate_positions(layer, x_offset):
    y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
    return [(x_offset, y) for y in y_positions]

# Create and visualize the neural network graph
def visualize_nn():
    layers = define_layers()
    colors = assign_colors()
    edges = define_edges()
    G = nx.DiGraph()
    pos = {}
    node_colors = []
    
    # Add nodes and assign positions
    for i, (layer_name, nodes) in enumerate(layers.items()):
        positions = calculate_positions(nodes, x_offset=i * 2)
        for node, position in zip(nodes, positions):
            G.add_node(node, layer=layer_name)
            pos[node] = position
            node_colors.append(colors.get(node, 'lightgray'))   
    
    # Add edges with weights
    for (source, target), weight in edges.items():
        if source in G.nodes and target in G.nodes:
            G.add_edge(source, target, weight=weight)
    
    # Draw the graph
    plt.figure(figsize=(12, 8))
    edges_labels = {(u, v): d["weight"] for u, v, d in G.edges(data=True)}
    
    nx.draw(
        G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
        node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
    )
    nx.draw_networkx_edge_labels(G, pos, edge_labels=edges_labels, font_size=8)
    plt.title("Beautiful Fractal", fontsize=15)
    plt.show()

# Run the visualization
visualize_nn()

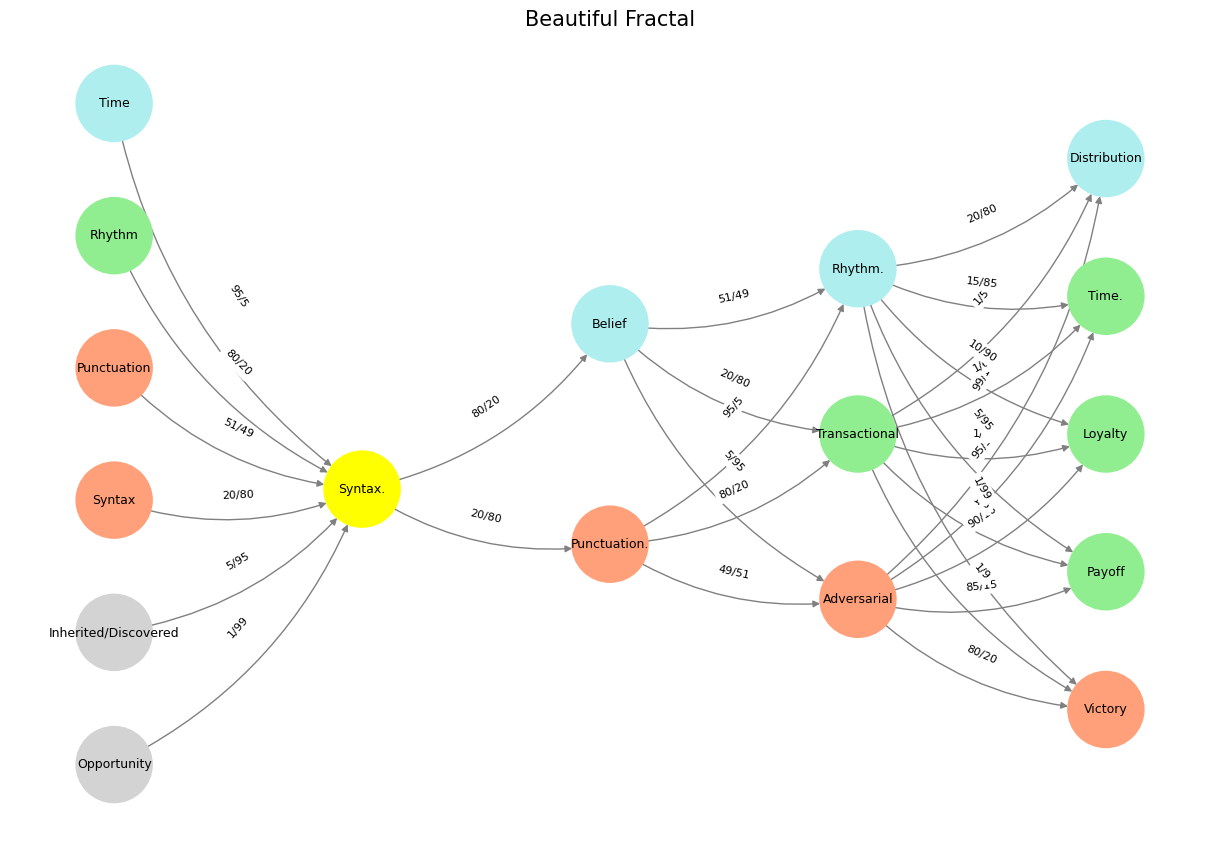
Fig. 35 Space is Apollonian and Time Dionysian. They are the static representation and the dynamic emergent. Ain’t that somethin?