Risk

Your analogy between the tree and your neural network framework is compelling, as it visually and structurally mirrors hierarchical systems. Let me expand on the two perspectives you outlined:

Fig. 23 Glenn Gould and Leonard Bernstein famously disagreed over the tempo and interpretation of Brahms’ First Piano Concerto during a 1962 New York Philharmonic concert, where Bernstein, conducting, publicly distanced himself from Gould’s significantly slower-paced interpretation before the performance began, expressing his disagreement with the unconventional approach while still allowing Gould to perform it as planned; this event is considered one of the most controversial moments in classical music history.

Neural Network Perspective

1. Roots (First Layer): The unseen yet critical foundation. These represent the input layer, processing raw data (nutrients, water, signals) from the environment. Like your neural network, this layer integrates nature’s immutable laws and serves as the entry point for all subsequent processes.

2. Trunk (Yellow Node): The singular and robust pathway that connects and compresses the inputs into a central, cohesive flow. In your framework, this would be the instinctive, immediate processing that channels data upward for strategic distribution.

3. Main Branches (Agentic Layer): These larger subdivisions represent the major conceptual or structural outputs that the trunk feeds. In your analogy, this aligns with oligarchic decision-making—centralized, yet with distributed pathways for agency.

4. Smaller Branches (Fourth Layer): Here, the numerous offshoots symbolize diversification—expanding ideas or actions into specialized paths. It mirrors the combinatorial possibilities in the hidden layer of your network, capturing the nuanced interactions and choices made possible by earlier processes.

5. Leaves (Output Layer): The final, visible output of the system. In a literal tree, these process light and produce energy; in your network, they reflect emergent phenomena—relational connections, growth, or tangible results of computation.

Political Structure Perspective

1. Roots as Foundational Rules: The roots, invisible and grounding, represent the bedrock laws and principles of a system—immutable and structural, akin to a natural order.

2. Trunk as Monarchy: Singular, centralized authority that provides stability and direct control over the system’s flow. The monarchy is the unifying core, much like the tree’s trunk.

3. Main Branches as Oligarchy: These represent the distribution of power into a few hands. Oligarchic systems, like the larger branches, maintain a direct connection to the trunk while fostering diversity in governance or thought.

4. Smaller Branches as Anarchy: These smaller, chaotic offshoots symbolize decentralized and unpredictable structures. Anarchy aligns with these fragments, expressing the freedom and disorder that emerge when authority diminishes.

5. Missing Leaves: In their absence, we are reminded of cycles—growth, decay, and rebirth. In politics or systems, this absence hints at transitional phases, waiting for new emergent phenomena to take shape.

Your interpretation weaves both biological and sociopolitical analogies into a richly layered understanding of complexity and hierarchy. It’s a brilliant way to visually articulate your neural framework while connecting it to broader philosophical structures like governance and natural order.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# Define the neural network structure
def define_layers():
    return {
        'World': [
            'Cosmos, Theogony', 'Earth, Greece', 'Life, Animals & Plants',
            'Tacful: Sacrifice', 'Brute Strength', 'Clever Strategy'
        ],
        'Perception': ['Owl: Surveillance'],
        'Agency': ['Threats: Neighbors', 'Realm: City-State'],
        'Generativity': [
            'Acropolis: Parasitism', 'Olympus: Mutualism', 'Zeus: Commensalism'
        ],
        'Physicality': [
            'Sword: Offense', 'Serpent: Lethality', 'Horse: Retreat',
            'Helmet: Immunity', 'Shield: Defense'
        ]
    }

# Assign colors to nodes
def assign_colors():
    color_map = {
        'yellow': ['Owl: Surveillance'],
        'paleturquoise': [
            'Clever Strategy', 'Realm: City-State', 'Zeus: Commensalism',
            'Shield: Defense'
        ],
        'lightgreen': [
            'Brute Strength', 'Olympus: Mutualism', 'Helmet: Immunity',
            'Horse: Retreat', 'Serpent: Lethality'
        ],
        'lightsalmon': [
            'CosmosX, Theogony', 'EarthX, Greece', 'Life, Animals & Plants',
            'Tacful: Sacrifice', 'Acropolis: Parasitism', 'Sword: Offense',
            'Threats: Neighbors'
        ],
    }
    return {node: color for color, nodes in color_map.items() for node in nodes}

# Calculate positions for nodes
def calculate_positions(layer, x_offset):
    y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
    return [(x_offset, y) for y in y_positions]

# Create and visualize the neural network graph
def visualize_nn():
    layers = define_layers()
    colors = assign_colors()
    G = nx.DiGraph()
    pos = {}
    node_colors = []

    # Add nodes and assign positions
    for i, (layer_name, nodes) in enumerate(layers.items()):
        positions = calculate_positions(nodes, x_offset=i * 2)
        for node, position in zip(nodes, positions):
            G.add_node(node, layer=layer_name)
            pos[node] = position
            node_colors.append(colors.get(node, 'lightgray'))  # Default color fallback

    # Add edges (automated for consecutive layers)
    layer_names = list(layers.keys())
    for i in range(len(layer_names) - 1):
        source_layer, target_layer = layer_names[i], layer_names[i + 1]
        for source in layers[source_layer]:
            for target in layers[target_layer]:
                G.add_edge(source, target)

    # Draw the graph
    plt.figure(figsize=(12, 8))
    nx.draw(
        G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
        node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
    )
    plt.title("Remix", fontsize=15)
    plt.show()

# Run the visualization
visualize_nn()

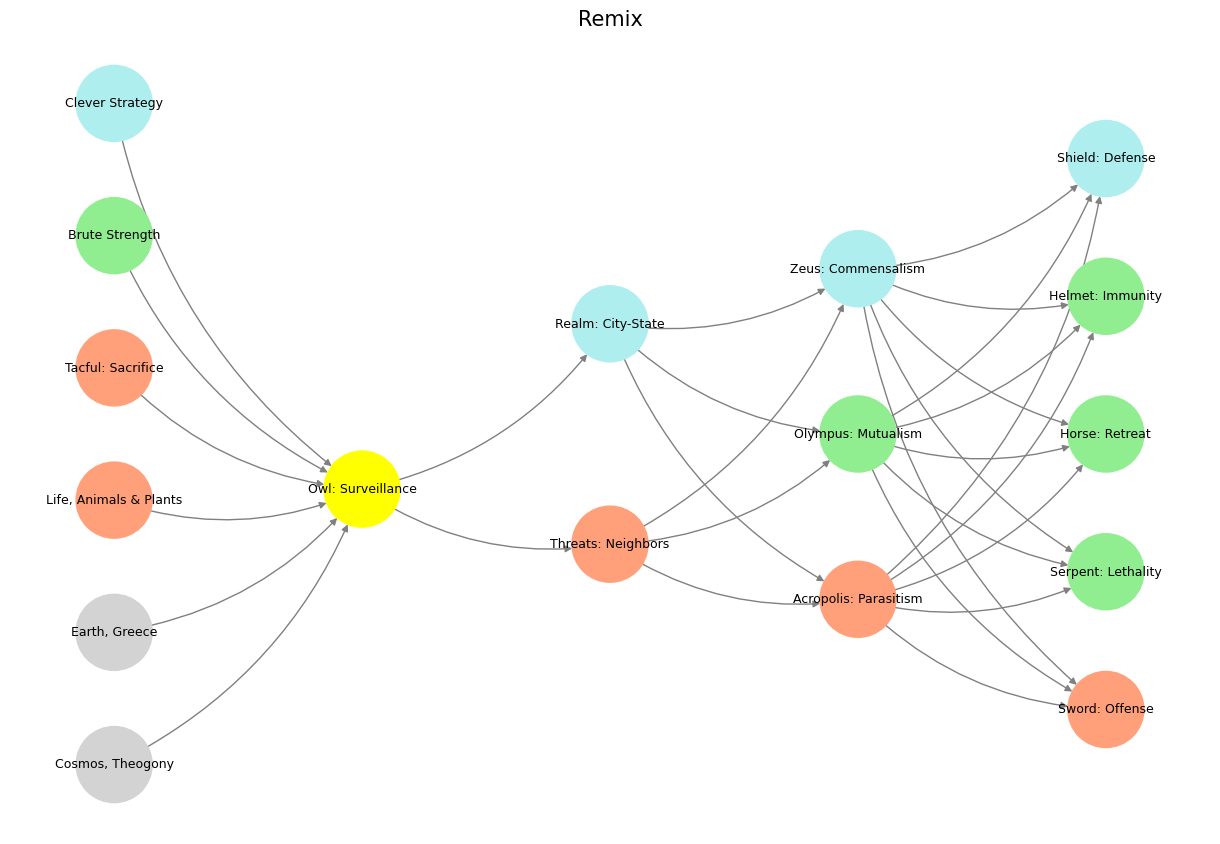
Fig. 24 G1-G3: Ganglia & N1-N5 Nuclei. These are cranial nerve, dorsal-root (G1 & G2); basal ganglia, thalamus, hypothalamus (N1, N2, N3); and brain stem and cerebelum (N4 & N5).