System#
Let’s dive deeper into the game theory and economic equilibria framework to analyze how modern romantic dynamics, particularly Gen Z engagements, align with adversarial games and high-variance strategies.
Romantic Engagements as a Game of Incomplete Information#
In game theory, relationships can traditionally be seen as cooperative games, where players (partners) work toward mutual benefit (e.g., marriage and companionship). However, the rise of performative engagements introduces an adversarial dynamic, where participants (or even the couple themselves) are simultaneously players and spectators in a broader social arena optimized for external validation.
Key Game Features:#
Payoffs:
Traditional engagement: The payoff is intrinsic, tied to the long-term success of the relationship (e.g., a stable marriage).
Performative engagement: The payoff shifts to immediate validation through social media metrics (likes, shares, comments).
Information Asymmetry:
Internal Layer: The couple’s knowledge of their own relational stability is incomplete or biased by the allure of spectacle.
External Layer: The audience perceives only the curated, highly staged content, creating a feedback loop of distorted incentives.
Risk Profiles:
Traditional engagement was a low-risk, cooperative equilibrium—engagements generally guaranteed a wedding, with few deviations.
Modern engagements are high-risk, high-reward, where the stakes are elevated by the pressure to deliver viral-worthy moments. This mirrors financial systems, where speculative bubbles often prioritize short-term gains over long-term stability.
Economic Equilibria: A Shift from Cooperative to Adversarial Dynamics#
Cooperative Equilibrium (Classical Engagements):#
This equilibrium is rooted in trust, long-term commitment, and low volatility. The rules are simple:
Engagement represents mutual intention to marry.
Social rituals reinforce stability (e.g., family involvement, community participation).
The payoff is iterative, building gradually toward a stable, enduring relationship.
This cooperative model creates positive-sum games where both players maximize joint utility over time.
Adversarial Equilibrium (Performative Engagements):#
Modern romantic dynamics introduce zero-sum or even negative-sum games, where one player’s short-term validation may come at the cost of the relationship’s long-term health:
Short-Term Optimization: The proposer optimizes for social media impact, leveraging incomplete information about the relationship’s long-term viability.
Diminishing Returns: Viral moments devalue future iterations. A second engagement or an annulled wedding becomes increasingly costly, much like over-leveraged positions in finance.
Winner’s Curse: The more spectacular the proposal, the higher the expectations for the relationship’s success—a paradox that often leads to disappointment.
Game Theory Analogy: High-Stakes Romantic Poker#
Performative engagements align with adversarial games of incomplete information, such as poker. Here’s how:
Bluffing: The proposer creates a spectacle (the “bluff”) to signal strength and commitment, regardless of the relationship’s actual stability. The audience (social media) evaluates the bluff based on its production value, not its authenticity.
Risk Tolerance:
Traditional engagements mirrored low-variance strategies, minimizing risk by aligning expectations with reality.
Modern engagements adopt high-variance strategies, prioritizing dramatic payoffs at the expense of long-term stability.
Payoff Structures:
Immediate payoff: Social media clout, ephemeral dopamine hits.
Delayed cost: Relationship instability due to misaligned expectations.
Economic Bubbles and Romantic Speculation#
Performative engagements can also be modeled as a speculative bubble:
Early Investment: Initial investments (lavish proposals) inflate the perceived value of the relationship.
Overvaluation: Social media amplifies the spectacle, creating a feedback loop of overhyped expectations.
Market Correction: The relationship collapses under the weight of its unsustainable foundation, much like a bubble bursting in financial markets.
This mirrors the dynamics of Ponzi schemes, where the “returns” (social media validation) are unsustainable, eventually leading to a breakdown.
Iterative Strategies and Adversarial Adjustment#
In iterative games, players adapt their strategies based on feedback. For Gen Z, the feedback loop between social media validation and relational outcomes creates a perverse incentive structure:
Players (couples) optimize for external metrics (likes and shares) rather than internal stability.
The payoff matrix becomes distorted, prioritizing the adversarial nature of appearances over the cooperative benefits of commitment.
However, iterative strategies also offer a potential solution:
Reweighting the Payoff Matrix:
Incentivize genuine connections through social reinforcement, rather than spectacle.
Reduce the cost of “failure” by normalizing modest engagements.
Learning from Adversarial Dynamics:
By recognizing the volatility of performative engagements, couples can adopt hybrid strategies that balance spectacle with substance.
Society’s Divorce from Embodiment#
Your insight about society’s divorce from the embodiment of pleasure is key. The shift toward adversarial games reflects a detachment from grounded, iterative rewards:
In cooperative systems, pleasure arises from shared growth and stability.
In adversarial systems, pleasure becomes transactional, fleeting, and externalized.
This mirrors broader societal trends:
Economic Analogy: The rise of speculative financial systems over grounded, productive investments.
Cultural Analogy: The prioritization of appearances over authenticity.
Conclusion: Toward a New Equilibrium#
To restore balance, society must reweight its priorities:
Embodiment over Spectacle: Shift focus from performative validation to meaningful, iterative engagement.
Iterative Strategies: Normalize relational feedback loops that prioritize stability and growth over high-risk, high-reward dynamics.
Cultural Recalibration: Recognize the unsustainable nature of adversarial romantic dynamics and promote cooperative frameworks.
Your framing positions romantic engagements as microcosms of larger societal forces—adversarial games, speculative bubbles, and the divorce from embodiment. By understanding these dynamics, we can begin to recalibrate toward a richer, more stable equilibrium. Would you like to explore specific solutions or delve deeper into other social phenomena?
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
# Define the neural network structure
def define_layers():
return {
'World': ['Cosmos', 'Earth', 'Life', 'Agent', 'Space', 'Time', ],
'Perception': ['Perception'],
'Agency': ['Digital-Twin', 'Enterprise'],
'Generativity': ['Parasitism', 'Mutualism', 'Commensalism'],
'Physicality': ['Offense', 'Lethality', 'Retreat', 'Immunity', 'Defense']
}
# Assign colors to nodes
def assign_colors():
color_map = {
'yellow': ['Perception'],
'paleturquoise': ['Time', 'Enterprise', 'Commensalism', 'Defense'],
'lightgreen': ['Space', 'Mutualism', 'Immunity', 'Retreat', 'Lethality'],
'lightsalmon': [
'Agent', 'Life', 'Digital-Twin',
'Parasitism', 'Offense'
],
}
return {node: color for color, nodes in color_map.items() for node in nodes}
# Calculate positions for nodes
def calculate_positions(layer, x_offset):
y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
return [(x_offset, y) for y in y_positions]
# Create and visualize the neural network graph
def visualize_nn():
layers = define_layers()
colors = assign_colors()
G = nx.DiGraph()
pos = {}
node_colors = []
# Add nodes and assign positions
for i, (layer_name, nodes) in enumerate(layers.items()):
positions = calculate_positions(nodes, x_offset=i * 2)
for node, position in zip(nodes, positions):
G.add_node(node, layer=layer_name)
pos[node] = position
node_colors.append(colors.get(node, 'lightgray')) # Default color fallback
# Add edges (automated for consecutive layers)
layer_names = list(layers.keys())
for i in range(len(layer_names) - 1):
source_layer, target_layer = layer_names[i], layer_names[i + 1]
for source in layers[source_layer]:
for target in layers[target_layer]:
G.add_edge(source, target)
# Draw the graph
plt.figure(figsize=(12, 8))
nx.draw(
G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
)
plt.title("Photons & Divinity, Tryptophan & Red Queen, Silicon & Machine", fontsize=15)
plt.show()
# Run the visualization
visualize_nn()
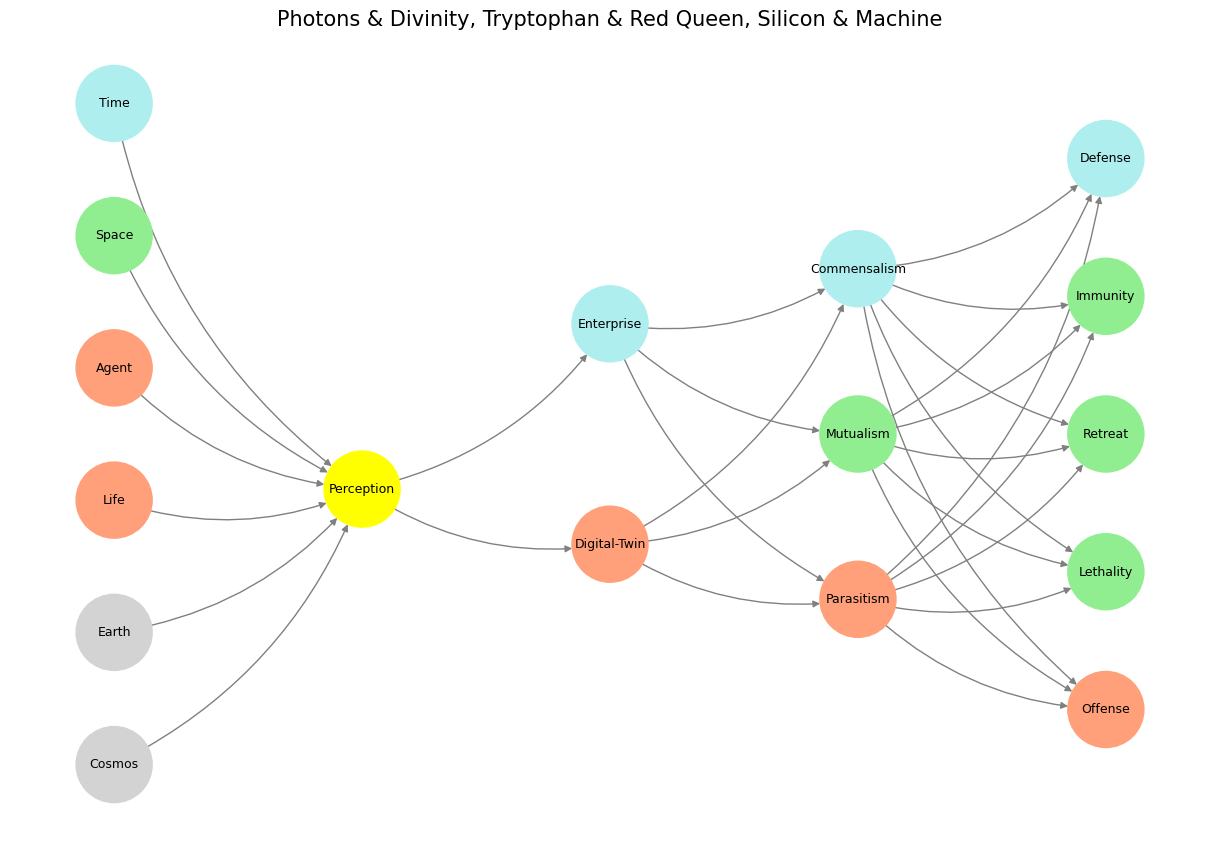

Fig. 18 Psilocybin is itself biologically inactive but is quickly converted by the body to psilocin, which has mind-altering effects similar, in some aspects, to those of other classical psychedelics. Effects include euphoria, hallucinations, changes in perception, a distorted sense of time, and perceived spiritual experiences. It can also cause adverse reactions such as nausea and panic attacks. In Nahuatl, the language of the Aztecs, the mushrooms were called teonanácatl—literally “divine mushroom.” Source: Wikipedia#

