Dancing in Chains#
Hubris and the Eternal Dance Between Static and Dynamic Equilibria#
Hubris, in its purest tragic form, is not merely the arrogance of mortals but the very catalyst that compels the interrogation of static versus dynamic equilibria. The tragic figure, whether Oedipus, Lear, or Faust, does not err by simple overreach; rather, they are caught in an inexorable feedback loop, where the laws of cosmos and cognition collide. To sin against these laws is to assert that trial and error must conclude, that the cadence should resolve, that the fugue should not spiral into perpetual transformation. But should it? Should tragedy culminate in Mozartean closure, a divine finality where order reasserts itself in crisp cadences, or does the nature of intelligence itself necessitate the eternally recurrent Wagnarian motif, the ceaseless modulation of theme upon theme?

Fig. 31 Freedom in Fetters—a Princely Freedom. Chopin, the last of the modern musicians, who gazed at and worshipped beauty, like Leopardi; Chopin, the Pole, the inimitable (none that came before or after him has a right to this name)—Chopin had the same princely punctilio in convention (grammar, space) that Raphael shows in the use of the simplest traditional colours. The only difference is that Chopin applies them not to colour but to melodic and rhythmic traditions (prosody, time). He admitted the validity of these traditions because he was born under the sway of etiquette. But in these fetters he plays and dances as the freest and daintiest of spirits, and, be it observed, he does not spurn the chain. Source: Human All-Too-Human Part II#
The Red Queen Hypothesis demands no respite; its claim is that stasis is death, that equilibrium in biology, in cognition, in physics, is always transient. Tragic hubris is often read as a moral failing, but perhaps it is something else entirely: an inevitability, the necessary price of refusing to accept an imposed equilibrium. If Oedipus had not sought the truth, if Macbeth had not defied the natural order, would their worlds have truly been preserved? Or would they have simply become the residue of a past iteration, swept away by the tide of history, irrelevant to the next game-theoretic step in the evolution of intelligence? The greatest tragedies are not lamentations of failure but requiems for the immutable, testaments to the violent necessity of iteration.
Yet, even as hubris propels the wheel forward, it carries a contradiction within itself. In its bold defiance of limit, does it not seek a higher form of permanence? If all things are trial and error, if no structure may persist without revision, what then of the immutable? Do the laws of the cosmos impose upon intelligence, biology, and physics the same necessity for fixity? The laws of thermodynamics remain unbroken, the speed of light unchallenged—should we then expect human cognition to find its own immutable laws, anchoring the ceaseless drift of intelligence and adaptation? If hubris is to be read not as mere error but as part of the loss function of intelligence itself, then the question is not whether we should stop running the Red Queen’s race but whether we can ever afford to.
Tragic figures are not merely cautionary tales; they are maps of the struggle between convergence and divergence, between rest and motion. The eternal recurrence of Wagnerian tonality whispers that there will be no final cadence, no rest from the necessity of adaptation. But does a system that never decelerates, that never rests, risk its own form of annihilation? If there is no stasis, is there ever meaning? The deeper tragedy of hubris may not be in its fall but in its function: it is the engine that guarantees we will never stand still, that the fugue will never resolve, that the final cadence will never arrive. If this is true, then our greatest sin is not hubris—it is the naive hope that trial and error will ever end.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
# Define the neural network layers
def define_layers():
return {
'Suis': ['Genome, 5%', 'Culture', 'Nourish It', 'Know It', "Move It", 'Injure It'], # Static
'Voir': ['Exposome, 15%'],
'Choisis': ['Metabolome, 50%', 'Basal Metabolic Rate'],
'Deviens': ['Unstructured-Intense', 'Weekly-Calendar', 'Proteome, 25%'],
"M'èléve": ['NexToken Prediction', 'Hydration', 'Fat-Muscle Ratio', 'Amor Fatì, 5%', 'Existential Cadence']
}
# Assign colors to nodes
def assign_colors():
color_map = {
'yellow': ['Exposome, 15%'],
'paleturquoise': ['Injure It', 'Basal Metabolic Rate', 'Proteome, 25%', 'Existential Cadence'],
'lightgreen': ["Move It", 'Weekly-Calendar', 'Hydration', 'Amor Fatì, 5%', 'Fat-Muscle Ratio'],
'lightsalmon': ['Nourish It', 'Know It', 'Metabolome, 50%', 'Unstructured-Intense', 'NexToken Prediction'],
}
return {node: color for color, nodes in color_map.items() for node in nodes}
# Define edge weights (hardcoded for editing)
def define_edges():
return {
('Genome, 5%', 'Exposome, 15%'): '1/99',
('Culture', 'Exposome, 15%'): '5/95',
('Nourish It', 'Exposome, 15%'): '20/80',
('Know It', 'Exposome, 15%'): '51/49',
("Move It", 'Exposome, 15%'): '80/20',
('Injure It', 'Exposome, 15%'): '95/5',
('Exposome, 15%', 'Metabolome, 50%'): '20/80',
('Exposome, 15%', 'Basal Metabolic Rate'): '80/20',
('Metabolome, 50%', 'Unstructured-Intense'): '49/51',
('Metabolome, 50%', 'Weekly-Calendar'): '80/20',
('Metabolome, 50%', 'Proteome, 25%'): '95/5',
('Basal Metabolic Rate', 'Unstructured-Intense'): '5/95',
('Basal Metabolic Rate', 'Weekly-Calendar'): '20/80',
('Basal Metabolic Rate', 'Proteome, 25%'): '51/49',
('Unstructured-Intense', 'NexToken Prediction'): '80/20',
('Unstructured-Intense', 'Hydration'): '85/15',
('Unstructured-Intense', 'Fat-Muscle Ratio'): '90/10',
('Unstructured-Intense', 'Amor Fatì, 5%'): '95/5',
('Unstructured-Intense', 'Existential Cadence'): '99/1',
('Weekly-Calendar', 'NexToken Prediction'): '1/9',
('Weekly-Calendar', 'Hydration'): '1/8',
('Weekly-Calendar', 'Fat-Muscle Ratio'): '1/7',
('Weekly-Calendar', 'Amor Fatì, 5%'): '1/6',
('Weekly-Calendar', 'Existential Cadence'): '1/5',
('Proteome, 25%', 'NexToken Prediction'): '1/99',
('Proteome, 25%', 'Hydration'): '5/95',
('Proteome, 25%', 'Fat-Muscle Ratio'): '10/90',
('Proteome, 25%', 'Amor Fatì, 5%'): '15/85',
('Proteome, 25%', 'Existential Cadence'): '20/80'
}
# Calculate positions for nodes
def calculate_positions(layer, x_offset):
y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
return [(x_offset, y) for y in y_positions]
# Create and visualize the neural network graph
def visualize_nn():
layers = define_layers()
colors = assign_colors()
edges = define_edges()
G = nx.DiGraph()
pos = {}
node_colors = []
# Create mapping from original node names to numbered labels
mapping = {}
counter = 1
for layer in layers.values():
for node in layer:
mapping[node] = f"{counter}. {node}"
counter += 1
# Add nodes with new numbered labels and assign positions
for i, (layer_name, nodes) in enumerate(layers.items()):
positions = calculate_positions(nodes, x_offset=i * 2)
for node, position in zip(nodes, positions):
new_node = mapping[node]
G.add_node(new_node, layer=layer_name)
pos[new_node] = position
node_colors.append(colors.get(node, 'lightgray'))
# Add edges with updated node labels
for (source, target), weight in edges.items():
if source in mapping and target in mapping:
new_source = mapping[source]
new_target = mapping[target]
G.add_edge(new_source, new_target, weight=weight)
# Draw the graph
plt.figure(figsize=(12, 8))
edges_labels = {(u, v): d["weight"] for u, v, d in G.edges(data=True)}
nx.draw(
G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edges_labels, font_size=8)
plt.title("OPRAH™: Heredity, Lifestyle, Badluck", fontsize=25)
plt.show()
# Run the visualization
visualize_nn()
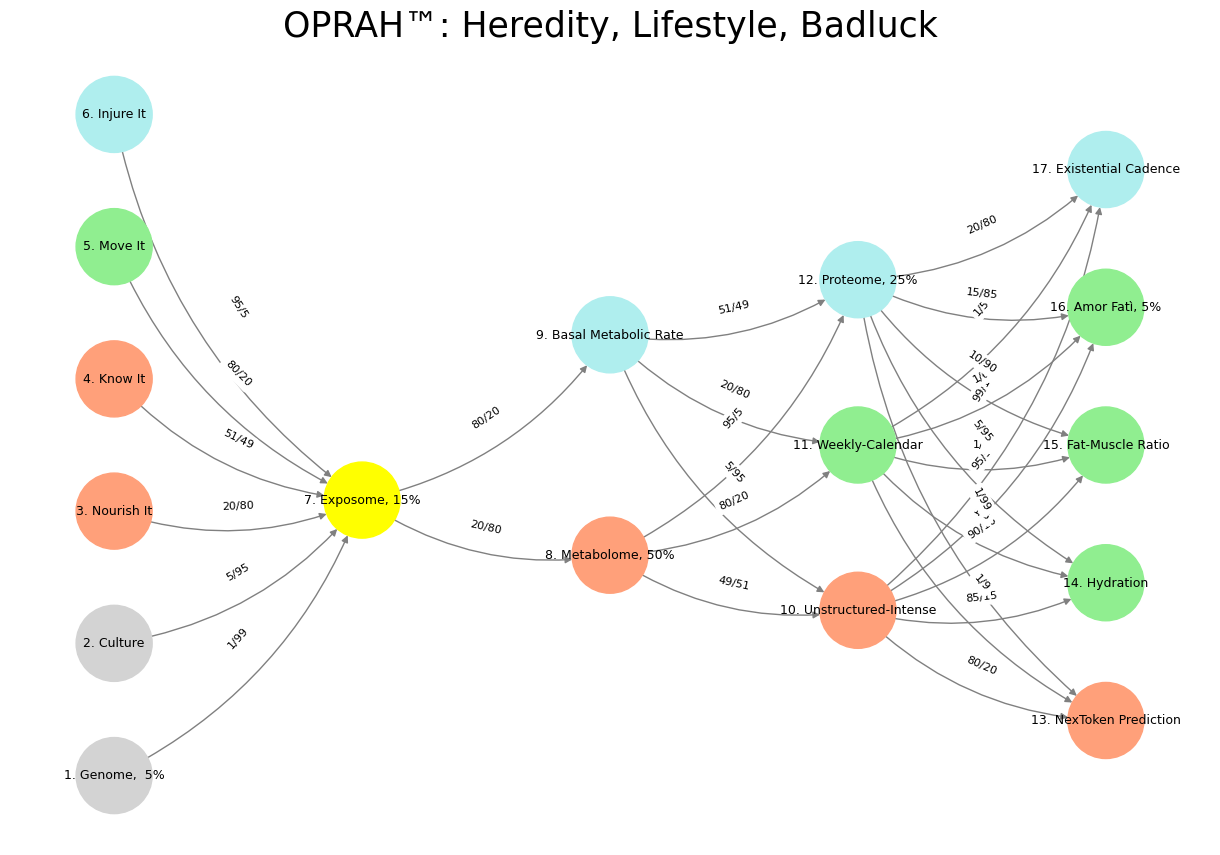

Fig. 32 G1-G3: Ganglia & N1-N5 Nuclei. These are cranial nerve, dorsal-root (G1 & G2); basal ganglia, thalamus, hypothalamus (N1, N2, N3); and brain stem and cerebelum (N4 & N5).#

