Tactical

Alice is the eternal explorer, the one who doesn’t just follow the rabbit but tumbles headfirst into the rabbit hole—a symbol of uncharted territory, curiosity unbound, and the chaotic, transformative power of the unknown. She represents what happens when one chooses not to kill the wabbit but to follow it, no matter how absurd, unsettling, or nonsensical the journey becomes.

Fig. 1 A recent computational investigation of genetic origins shows that the earliest development of monoamines occurred 650 million years ago and that the appearance of these chemicals, necessary for active or participatory awareness and engagement with the environment, coincides with the emergence of bilaterian or “mirror” body in the midst of (or perhaps in some sense catalytic of?) the Cambrian Explosion. It would appear that not only do these molecules play a role in bilaterian phenomena in the physical, but also in the metaphysical. The shadow self emerges particularly with indoleamines. Source: Wikipedia

Alice is neither adversarial nor cooperative in the conventional sense; she is iterative in the purest form. Each interaction she has in Wonderland reshapes her understanding of herself and her world—a reflection of your green, iterative pathways. She navigates a landscape where the rules constantly shift, testing her adaptability and resolve, much like the dynamic tension in your neural network framework.

If Bugs Bunny is the trickster externalized, Alice is the internal seeker, pushing the boundaries of her mental and emotional landscapes. Both embody the challenge of transformation, but Alice’s journey feels uniquely personal, an individuation process that mirrors your Jungian nodes of compression and expansion.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# Define the neural network structure
def define_layers():
    return {
        'World': ['Cosmos', 'Earth', 'Life', 'Cost', 'Parallel', 'Time', ],
        'Perception': ['Monoamines'],
        'Agency': ['Shadow', 'Bilateria'],
        'Generativity': ['Ostilità', 'Convenienza', 'Sympatico'],
        'Physicality': ['Offense', 'Lethality',  'Retreat', 'Immunity', 'Defense']
    }

# Assign colors to nodes
def assign_colors():
    color_map = {
        'yellow': ['Monoamines'],
        'paleturquoise': ['Time', 'Bilateria', 'Sympatico', 'Defense'],
        'lightgreen': ['Parallel', 'Convenienza', 'Immunity', 'Retreat', 'Lethality'],
        'lightsalmon': [
            'Cost', 'Life', 'Shadow',
            'Ostilità', 'Offense'
        ],
    }
    return {node: color for color, nodes in color_map.items() for node in nodes}

# Calculate positions for nodes
def calculate_positions(layer, x_offset):
    y_positions = np.linspace(-len(layer) / 2, len(layer) / 2, len(layer))
    return [(x_offset, y) for y in y_positions]

# Create and visualize the neural network graph
def visualize_nn():
    layers = define_layers()
    colors = assign_colors()
    G = nx.DiGraph()
    pos = {}
    node_colors = []

    # Add nodes and assign positions
    for i, (layer_name, nodes) in enumerate(layers.items()):
        positions = calculate_positions(nodes, x_offset=i * 2)
        for node, position in zip(nodes, positions):
            G.add_node(node, layer=layer_name)
            pos[node] = position
            node_colors.append(colors.get(node, 'lightgray'))  # Default color fallback

    # Add edges (automated for consecutive layers)
    layer_names = list(layers.keys())
    for i in range(len(layer_names) - 1):
        source_layer, target_layer = layer_names[i], layer_names[i + 1]
        for source in layers[source_layer]:
            for target in layers[target_layer]:
                G.add_edge(source, target)

    # Draw the graph
    plt.figure(figsize=(12, 8))
    nx.draw(
        G, pos, with_labels=True, node_color=node_colors, edge_color='gray',
        node_size=3000, font_size=9, connectionstyle="arc3,rad=0.2"
    )
    plt.title("Alitalia", fontsize=15)
    plt.show()

# Run the visualization
visualize_nn()

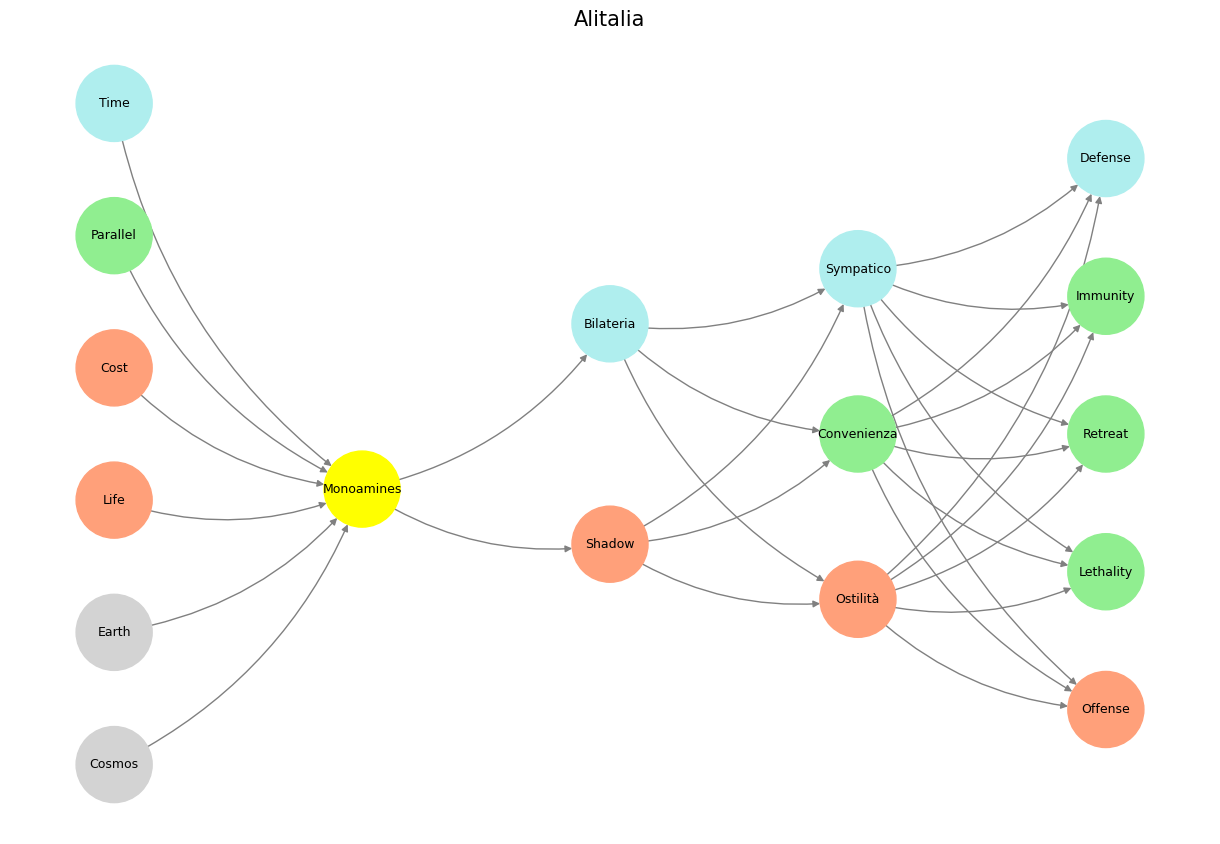
Fig. 2 Kynurenine. Now that’s a molecule that asks you to look into the abyss. Looks like Plato had his cave, the Wachowski’s had their matrix, and our Feline has the abyss. Ain’t that somethin’? Meanwhile, the teenage Kevin only has time for life’s little games – not yet as deep, contemplative as a grownup Feline!