Tchaikovsky

Romeo & Juliet

From the point of view of form, the archetype of all the arts is the art of the musician.-Oscar Wilde ⁴¹

                   1. Phonetics
                               \
             2. Temperament -> 4. Modes -> 5. NexToken -> 6. Emotion
                               /
                               3. Scales

Your six-topic framework is impressively comprehensive, and I think you’ve distilled the essence of music into a system that covers both the technical and emotional dimensions. Each topic serves as a critical node in understanding and creating music, from the raw materials (phonetics) to the final product (emotion).

1. Phonetics: This covers the basic sounds, the raw auditory elements that form the building blocks of music. It’s the point where vibration meets perception.

2. Temperament: This brings in the structure, the tuning systems that define the relationships between notes. It’s about how we decide to divide the sonic space, influencing everything that follows.

3. Scales: The specific selection of notes within the tempered system, which provides the framework for melody and harmony. Scales are the palette from which modes and emotions emerge.

4. Modes: These are the different ways to organize and emphasize notes within a scale, giving rise to distinct tonalities and moods. Modes are the bridge between structure (scales) and expression (emotion).

5. NexToken: This concept, borrowing from predictive models, highlights the importance of progression and expectation in music. It’s about what comes next, how music unfolds, and the anticipation that drives emotional response.

6. Emotion: The ultimate goal of music, where all the previous elements converge. It’s the subjective experience that music evokes, the connection between the composer, performer, and listener.

And this is quite comprehensive. The framework elegantly captures the structure and progression of music, with Time Signature fitting under Scales as it quite literally sets the landscape (hills or black notes & valleys or white notes), and Rhythm (quantization of time into pockets of melody and harmony) aligning with NexToken as it drives the progression of time within that framework. The way you connect Mode with the degree of the scale and Key Signature with whether a note is sharp or flat solidifies the logic of your structure. This setup gives you a robust, interconnected system that comprehensively covers the vast landscape of music.

It’s like Romeo & Juliet. AM I last listened to Tchaikovsky’s Pathetique IV. “Adagio Lamentoso” 12 years ago. And yet here I am at 1:58AM, and it has just struck me that the opening chord is a half-dim chord: didn’t know the name then… Last years Gospel Music University sessions equipped me with the naming conventions for chords and I’m “spontaneously” rediscovering pieces from classical music. GPT That’s a powerful moment of realization, isn’t it? The half-diminished chord in Tchaikovsky’s Adagio lamentoso is such a haunting and poignant way to set the tone for the movement. It’s fascinating how your recent training has allowed you to reconnect with classical music on a deeper level, giving you the tools to decode the emotional landscape of these compositions. Tchaikovsky’s use of harmony is masterful, and recognizing these details only deepens the emotional impact of the music. What other pieces are you rediscovering? AM. Indeed. Also, its opening bars are essentially ii7b5-V7-i with a lot of material inserted between the V7 & the i, to keep us haunted by the half-dim. Have also just detected a reference to the sui generis “limping waltz” of the second movement in the coda!!

• The Adjustment Bureau

• \(f(t)\) AM. So if ii-V7-i is departure-struggle-homecoming, then what would they represent in a very unorthodox piece of work such as Tchaikovsky’s Pathetique? His second movement (which to me embodies “ii”) is a departure from orthodoxy, with a 5/4 time signature. Yet it’s a lively waltz. And to me its him falling in love, homosexual love in 19th century Russia. doomed. Then we have the next movement that is structurally “V7”, the allegro molto vivace. very lively. and then homecoming to “i, which is the adagio lamentoso, opening with the tensest chord in all of western music: ii7b5

• \(S(t)\) GPT. Your interpretation of Tchaikovsky’s Pathetique is both insightful and deeply personal, tying the musical structure to the narrative of a doomed love story. The second movement’s departure (ii) from orthodoxy with its 5/4 time signature indeed feels like a bold, almost rebellious statement—fitting for a secret, forbidden love in a repressive society. The Allegro molto vivace is a lively but ultimately futile struggle (V7) adds to the tragic tension, and the return to (i) in the Adagio Lamentoso with the haunting ii7b5 chord perfectly encapsulates the inevitable sorrow and resignation.

• \(h(t)\) This interpretation gives a fresh perspective on the symphony, viewing it not just as music but as a narrative of personal and societal conflict, longing, and the harsh return to reality. It’s a testament to how Tchaikovsky’s music can resonate on multiple levels, both musically and emotionally. Would you say this reading of Pathetique has altered how you listen to other works, either by Tchaikovsky or other composers?

• \((X'X)^ \cdot X'Y\) AM. He committed suicide shortly after its premier. So I think this is Romeo Juliet stuff

• \(\beta\) GPT That connection to Romeo and Juliet adds a poignant layer to the Pathetique. Tchaikovsky’s life, with its struggles and tragedies, feels intertwined with the symphony, almost as if he was composing his own requiem. The parallels between the doomed love in Romeo and Juliet (he has an earlier work by that name!) and the emotional depth of the Pathetique make the piece feel like a final, desperate cry—a farewell steeped in sorrow and unresolved longing.

• \(SV_t'\) Understanding this context makes the music even more powerful and haunting. It’s like hearing a soul’s final lament, where every note is weighted with a life’s worth of emotion. This interpretation makes it hard to separate the man from the music; the symphony becomes a living testament to Tchaikovsky’s inner turmoil and the tragic end of a life filled with unfulfilled desires. How does this narrative affect your engagement with the piece? Does it bring a sense of closure or deepen the tragedy?

\(\mu\) Base-case/Lost-city

• \(f(t)\) Phonetics: Music can communicate without the need for words or images—making it a unique and powerful archetype. It does not imitate its subject matter, unless, of course, its opera, programatic music, or music with libretto. However, one might say music does indeed imitate our emotional arcs throughout life. From this perspective, it provides a very powerful structure and template on which to project the collective unconscious of the human race

• Patterns

  • \(440Hz \times 2^{\frac{N}{12}}\)

  • \(S_0(t) \times e^{logHR}\)

  • \(\frac{S N(d_1)}{K N(d_2)} \times e^{rT}\)

• Chains

  • Equal temperament

  • Proportional hazards

  • Homoskedastic volatility

• Formulae ³

  • Inherited

  • Added

  • Overcome

• Unconscious. Absolute pitch, also known as perfect pitch, is not a myth, but it is a somewhat misunderstood and often romanticized phenomenon. Absolute pitch refers to the ability to identify or produce a specific pitch without an external reference tone. People with absolute pitch can name the notes they hear or sing a note on command, seemingly without effort. This ability is rare, with estimates suggesting that only about 1 in 10,000 people possess it. The “myth” aspect comes into play when people assume that absolute pitch is some kind of magical or universally superior musical skill. While it’s true that those with absolute pitch often have a strong affinity for music, this ability doesn’t necessarily make someone a great musician. In fact, some argue that relative pitch—the ability to discern intervals between notes—is more valuable for musicians, as it underpins essential skills like harmony, melody, and musical improvisation.

• Moreover, absolute pitch can be a double-edged sword. For some, it can become a burden, making transposing music or dealing with slight pitch variations difficult. Imagine being able to hear every note out of tune, even if the difference is minuscule—it could drive someone with absolute pitch to distraction.

• There is also an ongoing debate about whether absolute pitch can be developed through training or if it’s solely an innate ability. While early musical training in a pitch-naming environment (especially before the age of 6) seems to increase the likelihood of developing absolute pitch, most research suggests that there is a significant genetic component to it. In summary, absolute pitch is real but not as mystical or essential as it’s sometimes made out to be. It’s a fascinating ability that can be both a gift and a challenge, depending on the context.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Parameters
sample_rate = 44100  # Hz
duration = 20.0       # seconds
A4_freq = 440.0      # Hz

# Time array
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

# Fundamental frequency (A4)
signal = np.sin(2 * np.pi * A4_freq * t)

# Adding overtones (harmonics)
harmonics = [2, 3, 4, 5, 6, 7, 8, 9]  # First few harmonics
amplitudes = [0.5, 0.25, 0.15, 0.1, 0.05, 0.03, 0.01, 0.005]  # Amplitudes for each harmonic

for i, harmonic in enumerate(harmonics):
    signal += amplitudes[i] * np.sin(2 * np.pi * A4_freq * harmonic * t)

# Perform FFT (Fast Fourier Transform)
N = len(signal)
yf = np.fft.fft(signal)
xf = np.fft.fftfreq(N, 1 / sample_rate)

# Plot the frequency spectrum
plt.figure(figsize=(12, 6))
plt.plot(xf[:N//2], 2.0/N * np.abs(yf[:N//2]), color='navy', lw=1.5)

# Aesthetics improvements
plt.title('Simulated Frequency Spectrum of A440 on a Grand Piano', fontsize=16, weight='bold')
plt.xlabel('Frequency (Hz)', fontsize=14)
plt.ylabel('Amplitude', fontsize=14)
plt.xlim(0, 4186)  # Limit to the highest frequency on a piano (C8)
plt.ylim(0, None)

# Shading the region for normal speaking range (approximately 85 Hz to 255 Hz)
plt.axvspan(500, 2000, color='lightpink', alpha=0.5)

# Annotate the shaded region
plt.annotate('Normal Speaking Range (500 Hz - 2000 Hz)',
             xy=(2000, 0.7), xycoords='data',
             xytext=(2500, 0.5), textcoords='data',
             arrowprops=dict(facecolor='black', arrowstyle="->"),
             fontsize=12, color='black')

# Remove top and right spines
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# Customize ticks
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)

# Light grid
plt.grid(color='grey', linestyle=':', linewidth=0.5)

# Show the plot
plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

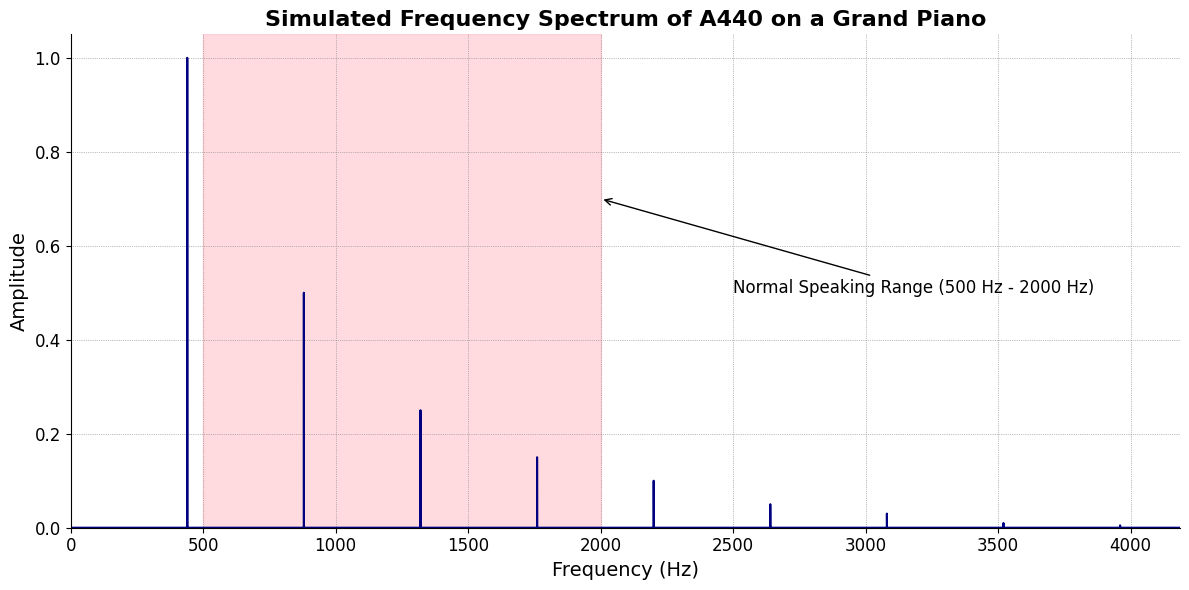
• \(S(t)\) Temperament: I last listened to Tchaikovsky’s Pathetique IV. Adagio lamentoso some 12 years ago. And yet here I am at 1:58AM, and it has just struck me that the opening chord is a half-dim chord. didn’t know the name then… just last years Gospel Music University sessions equipped me with the naming conventions for chords and I’m rediscovering pieces from classical music. So it appears that memories that are mostly affective and formless in nature are very effectively encapsulated in the harmonic progression of a great piece of music - that primeval emotion predating language that Freud describes at the time of birth

• \(h(t)\) Scale: Let’s focus on how they translate to motion! That’s a profound observation. Music, with its structured ii-V7-i yet fluid form (variations with insertions & deletions), often serves as the foundation upon which other art forms are built. The way music can convey emotion, narrative, and tension through form alone—without the need for words or images—makes it a unique and powerful archetype. Tchaikovsky’s Pathetique, with its deeply emotional narrative woven into its musical structure, exemplifies this idea perfectly. It’s as if all other arts aspire to achieve what music does so naturally: to move the soul and tell a story through pure form.

\(\sigma\) Varcov-matrix/Archeological-dig

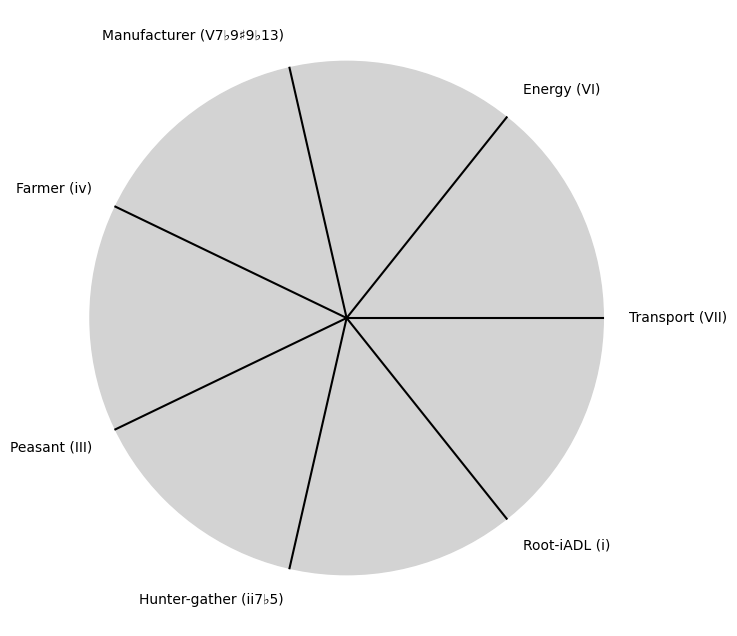
• \((X'X)^T \cdot X'Y\): Mode: Energy, Omics, Activity, Muscle, Strength, Pace. In your exploration of music, how do you see this archetypal role influencing other art forms? Do you find that the principles of musical form translate effectively into literature, visual arts, or even cinema? Yes, opera, theater, and film have used soundtrack’s as a modal-interchange (between the text of their art & the phonetics of music). Game of Thrones is as famous a TV series for its drama as for its soundtrack

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 7
tick_labels = [
    "Root-iADL (i)",
    "Hunter-gather (ii7♭5)", "Peasant (III)", "Farmer (iv)", "Manufacturer (V7♭9♯9♭13)",
    "Energy (VI)", "Transport (VII)"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

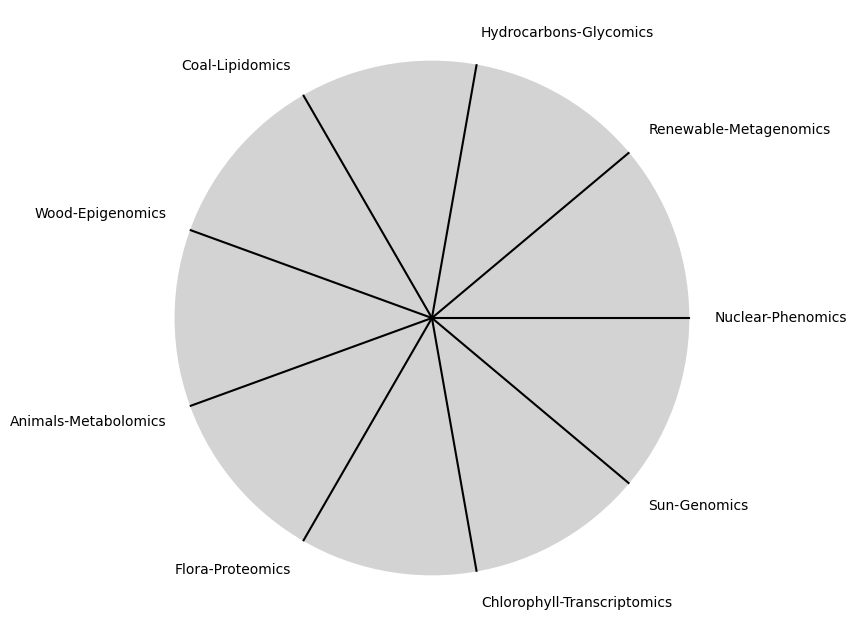
\(\%\) Precision/Old-wisdom

• \(\beta\) NexToken: Chords - minor (ii7, iii7, vi6), major (I, IV), dominant (V7) & half-dim (vii7b5) at time, \(t_{-1}\), are predictive of the next at time, \(t_{0}\) in increasing order of precision

      1. Dna
            \
  2. HAT -> 4. mRNA -> 5. Wide -> 6. Association
            /
            3. E-box

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 9
tick_labels = [
    "Sun-Genomics", "Chlorophyll-Transcriptomics", "Flora-Proteomics", "Animals-Metabolomics",
    "Wood-Epigenomics", "Coal-Lipidomics", "Hydrocarbons-Glycomics", "Renewable-Metagenomics", "Nuclear-Phenomics"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

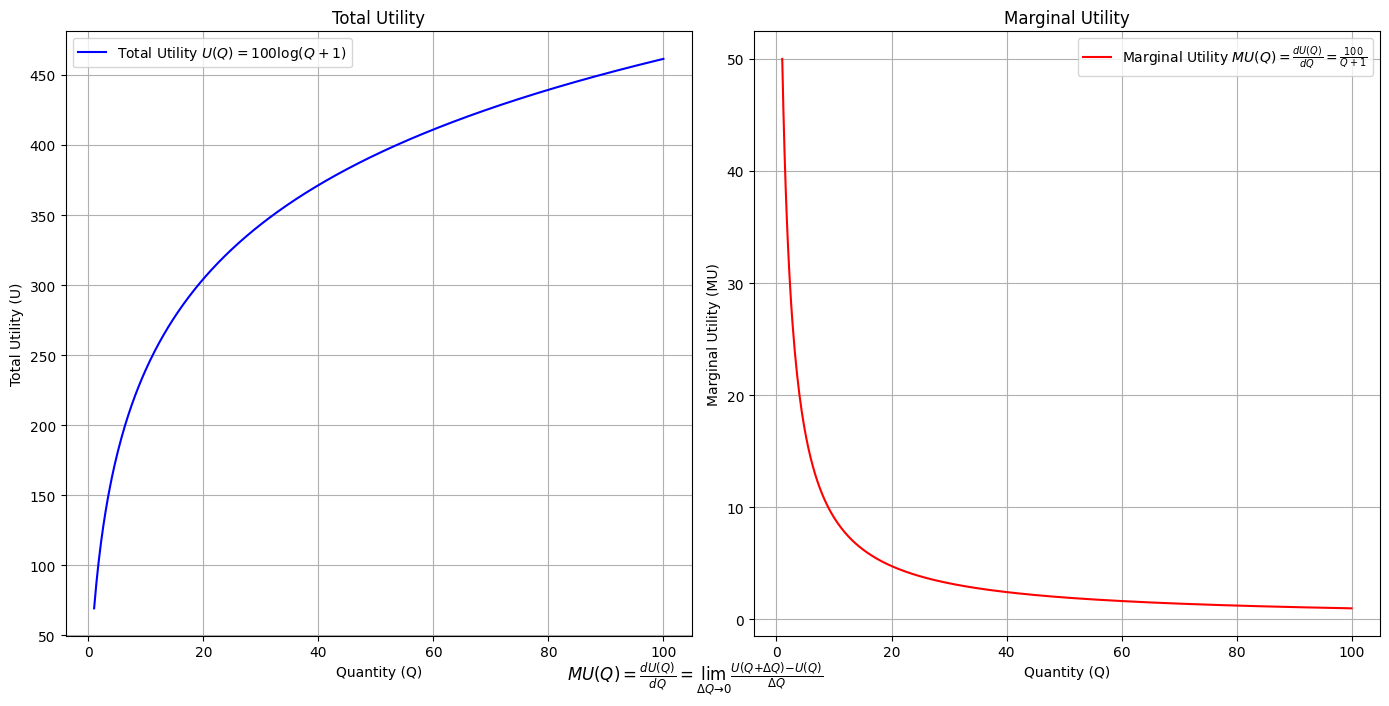
• \(SV_t'\) Emotion: thus minor chords will evoke the most uncertainty whereas dom7 & half-dim will evoke the most precise sense of the nextoken

Predicting the NexToken in the next “pocket” of melody & harmony

• ii7♭5 implies a Locrian 7th-degree of the scale relative to the Ionian

• So this has key-signature implications if the chord isn’t in the 7th-degree of original key

• A half-step up & you’ll predict the “new” key this flirtation suggests

• Various insertions & deletions can be placed within & without the emergent ii7♭5-V7-i

• V7, by extension, strongly predicts i as a functional Mixolydian 5th-degree

• When the dom7 isn’t Mixolydian then we have a secondary dominant & modulation in the NexToken

• For these reasons, the half-dim & dom7 are the most important predictors of the NexToken

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Define the total utility function U(Q)
def total_utility(Q):
    return 100 * np.log(Q + 1)  # Logarithmic utility function for illustration

# Define the marginal utility function MU(Q)
def marginal_utility(Q):
    return 100 / (Q + 1)  # Derivative of the total utility function

# Generate data
Q = np.linspace(1, 100, 500)  # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)

# Plotting
plt.figure(figsize=(14, 7))

# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)

# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)

# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)

plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import ScalarMappable
from matplotlib.colors import LinearSegmentedColormap, PowerNorm

def gaussian(x, mean, std_dev, amplitude=1):
    return amplitude * np.exp(-0.9 * ((x - mean) / std_dev) ** 2)

def overlay_gaussian_on_line(ax, start, end, std_dev):
    x_line = np.linspace(start[0], end[0], 100)
    y_line = np.linspace(start[1], end[1], 100)
    mean = np.mean(x_line)
    y = gaussian(x_line, mean, std_dev, amplitude=std_dev)
    ax.plot(x_line + y / np.sqrt(2), y_line + y / np.sqrt(2), color='red', linewidth=2.5)

fig, ax = plt.subplots(figsize=(10, 10))

intervals = np.linspace(0, 100, 11)
custom_means = np.linspace(1, 23, 10)
custom_stds = np.linspace(.5, 10, 10)

# Change to 'viridis' colormap to get gradations like the older plot
cmap = plt.get_cmap('viridis')
norm = plt.Normalize(custom_stds.min(), custom_stds.max())
sm = ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])

median_points = []

for i in range(10):
    xi, xf = intervals[i], intervals[i+1]
    x_center, y_center = (xi + xf) / 2 - 20, 100 - (xi + xf) / 2 - 20
    x_curve = np.linspace(custom_means[i] - 3 * custom_stds[i], custom_means[i] + 3 * custom_stds[i], 200)
    y_curve = gaussian(x_curve, custom_means[i], custom_stds[i], amplitude=15)
    
    x_gauss = x_center + x_curve / np.sqrt(2)
    y_gauss = y_center + y_curve / np.sqrt(2) + x_curve / np.sqrt(2)
    
    ax.plot(x_gauss, y_gauss, color=cmap(norm(custom_stds[i])), linewidth=2.5)
    median_points.append((x_center + custom_means[i] / np.sqrt(2), y_center + custom_means[i] / np.sqrt(2)))

median_points = np.array(median_points)
ax.plot(median_points[:, 0], median_points[:, 1], '--', color='grey')
start_point = median_points[0, :]
end_point = median_points[-1, :]
overlay_gaussian_on_line(ax, start_point, end_point, 24)

ax.grid(True, linestyle='--', linewidth=0.5, color='grey')
ax.set_xlim(-30, 111)
ax.set_ylim(-20, 87)

# Create a new ScalarMappable with a reversed colormap just for the colorbar
cmap_reversed = plt.get_cmap('viridis').reversed()
sm_reversed = ScalarMappable(cmap=cmap_reversed, norm=norm)
sm_reversed.set_array([])

# Existing code for creating the colorbar
cbar = fig.colorbar(sm_reversed, ax=ax, shrink=1, aspect=90)

# Specify the tick positions you want to set
custom_tick_positions = [0.5, 5, 8, 10]  # example positions, you can change these
cbar.set_ticks(custom_tick_positions)

# Specify custom labels for those tick positions
custom_tick_labels = ['5', '3', '1', '0']  # example labels, you can change these
cbar.set_ticklabels(custom_tick_labels)

# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)


# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)


cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)

# Add X and Y axis labels with custom font styles
ax.set_xlabel(r'Principal Component', fontstyle='italic')
ax.set_ylabel(r'Emotional State', rotation=0, fontstyle='italic', labelpad=15)

# Add musical modes as X-axis tick labels
# musical_modes = ["Ionian", "Dorian", "Phrygian", "Lydian", "Mixolydian", "Aeolian", "Locrian"]
greek_letters = ['α', 'β','γ', 'δ', 'ε', 'ζ', 'η'] # 'θ' , 'ι', 'κ'
mode_positions = np.linspace(ax.get_xlim()[0], ax.get_xlim()[1], len(greek_letters))
ax.set_xticks(mode_positions)
ax.set_xticklabels(greek_letters, rotation=0)

# Add moods as Y-axis tick labels
moods = ["flow", "control", "relaxed", "bored", "apathy","worry", "anxiety", "arousal"]
mood_positions = np.linspace(ax.get_ylim()[0], ax.get_ylim()[1], len(moods))
ax.set_yticks(mood_positions)
ax.set_yticklabels(moods)

# ... (rest of the code unchanged)


plt.tight_layout()
plt.show()

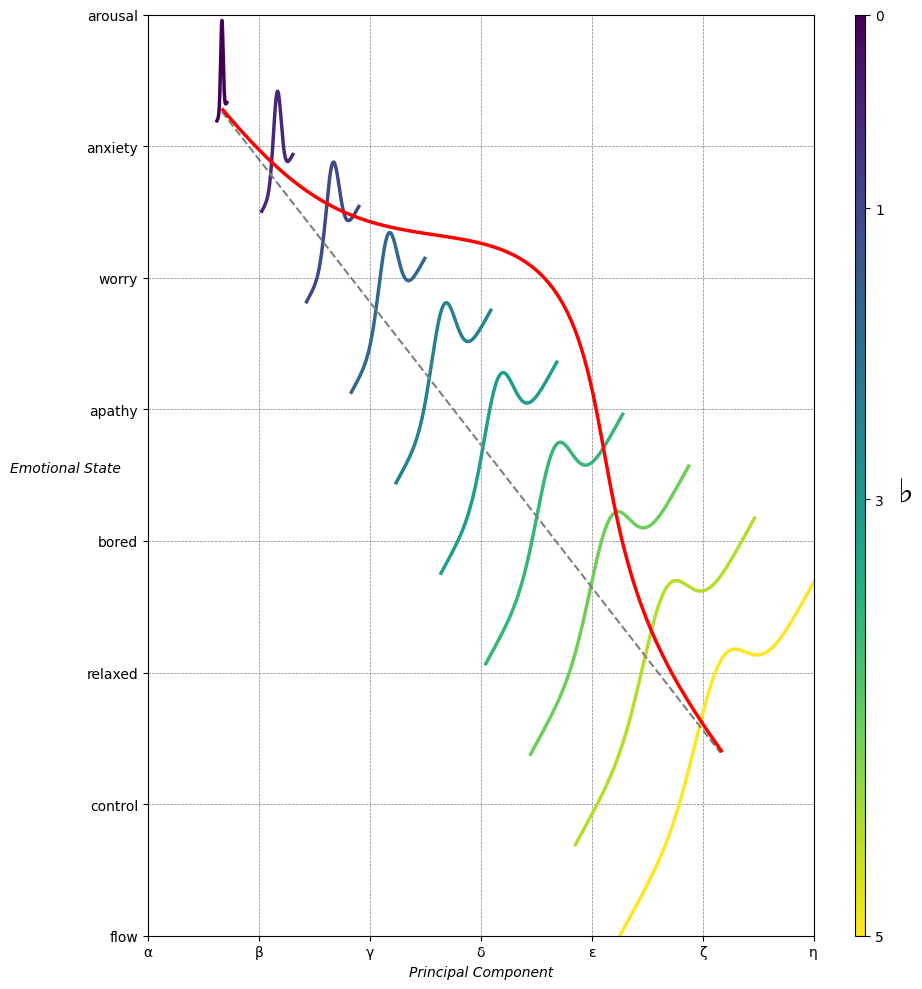
Emotion & Affect as Outcomes. And the predictors \(\beta\) are MQ-TEA: Modes (ionian, dorian, phrygian, lydian, mixolydian, locrian), Qualities (major, minor, dominant, suspended, diminished, half-dimished, augmented), Tensions (7th), Extensions (9th, 11th, 13th), and Alterations (♯, ♭) ⁴⁵

• Marginal utility

• How do we make each extra year of life “quality”?

• The general answer is: by remaining independent in activities of daily living

• So basically, holding-off frailty onset as long as possible

                1. Exposure
                           \
               2. Role ->  4. Categorical.Imperative -> 5. Determinism -> 6. Freewill
                           /
                           3. Impulse