Bureau

Philosophy

From the point of view of form, the archetype of all the arts is the art of the musician.-Oscar Wilde ²⁴

                1. f(t)
                       \
            2. S(t) -> 4. y:h'(t)=0;t(X'X).X'Y -> 5. b -> 6. SV'
                       /
                       3. h(t)

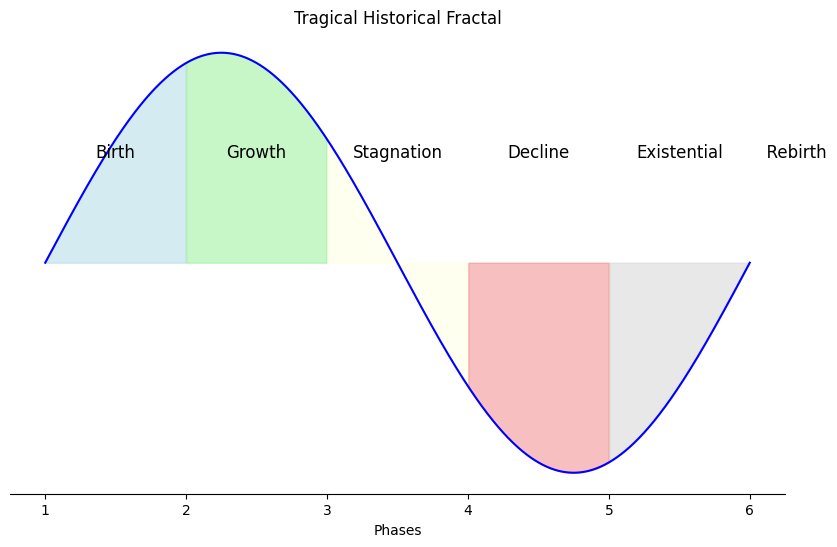
What happened to Free Will?. Who said anything about Free Will? You know, we actually tried Free Will before. After taking you from hunting and gathering to the height of the Roman Empire we stepped back to see how you’d do on your own.You gave us the Dark Ages – for five centuries – until finally we decided we should come back in.

• The Adjustment Bureau

• The tension between emotion, impulse, and action \(h(t)\) versus

• Duty, rules, and tradition \(S(t)\)

• A classic struggle that defines much of human experience \(f(t)\). It’s the stuff of great drama, literature, and philosophy—a war within the self that pits personal desires and instincts against the expectations and obligations imposed by society.

• This conflict is often portrayed in narratives where characters are forced to choose between following their heart and adhering to the norms of the group, be it a family, community, or institution. The “Adjustment Bureau” you mentioned, whether metaphorical or literal, represent the forces that attempt to maintain order by curbing individuality and ensuring conformity in line with the categorical imperative. They’re like the unseen hands of fate, working to suppress or redirect those impulses that threaten the stability of the collective unconscious \((X'X)^T \cdot X'Y\).

• In many ways, this struggle reflects the larger theme of free will \(SV_t'\) versus

• Determinism \(\beta\). Are we free to act on our emotions and impulses, or are we bound by the duties and traditions we’ve inherited? The beauty and tragedy of this conflict lie in the fact that there’s no simple resolution—it’s an eternal push and pull, where the outcome is never certain. Characters who wrestle with this dilemma are often the most compelling because they embody the human condition in its rawest form. They challenge the status quo, disrupt the carefully maintained order, and force a reckoning between personal authenticity and societal expectations. And in this clash, there’s often no clear winner, just a deeper understanding of the costs and consequences of choosing one path over the other.

\(\mu\) Base-case

• Senses: Curated

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Parameters
sample_rate = 44100  # Hz
duration = 20.0       # seconds
A4_freq = 440.0      # Hz

# Time array
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

# Fundamental frequency (A4)
signal = np.sin(2 * np.pi * A4_freq * t)

# Adding overtones (harmonics)
harmonics = [2, 3, 4, 5, 6, 7, 8, 9]  # First few harmonics
amplitudes = [0.5, 0.25, 0.15, 0.1, 0.05, 0.03, 0.01, 0.005]  # Amplitudes for each harmonic

for i, harmonic in enumerate(harmonics):
    signal += amplitudes[i] * np.sin(2 * np.pi * A4_freq * harmonic * t)

# Perform FFT (Fast Fourier Transform)
N = len(signal)
yf = np.fft.fft(signal)
xf = np.fft.fftfreq(N, 1 / sample_rate)

# Plot the frequency spectrum
plt.figure(figsize=(12, 6))
plt.plot(xf[:N//2], 2.0/N * np.abs(yf[:N//2]), color='navy', lw=1.5)

# Aesthetics improvements
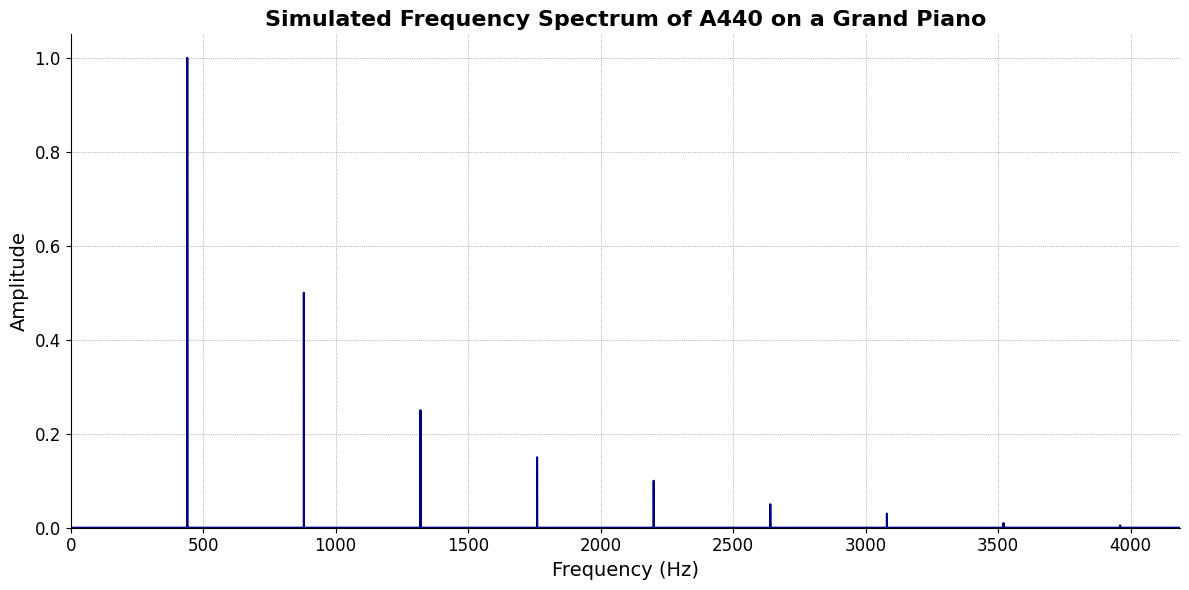
plt.title('Simulated Frequency Spectrum of A440 on a Grand Piano', fontsize=16, weight='bold')
plt.xlabel('Frequency (Hz)', fontsize=14)
plt.ylabel('Amplitude', fontsize=14)
plt.xlim(0, 4186)  # Limit to the highest frequency on a piano (C8)
plt.ylim(0, None)

# Remove top and right spines
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# Customize ticks
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)

# Light grid
plt.grid(color='grey', linestyle=':', linewidth=0.5)

# Show the plot
plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

• Memory: Luxury

• Emotions: Numbed

\(\sigma\) Varcov-matrix

• Evolution: Society ²

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 7
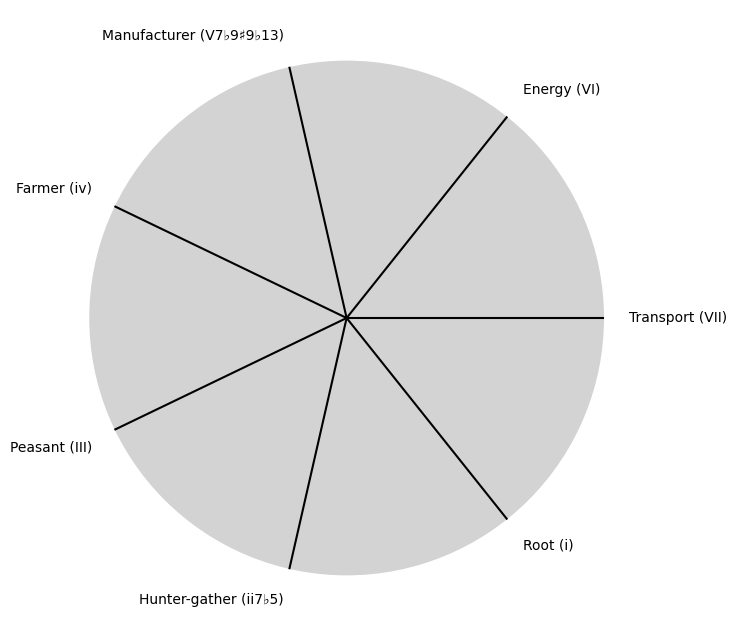
tick_labels = [
    "Root (i)",
    "Hunter-gather (ii7♭5)", "Peasant (III)", "Farmer (iv)", "Manufacturer (V7♭9♯9♭13)",
    "Energy (VI)", "Transport (VII)"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

\(\%\) Precision

• Needs: God-man-ai

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 9
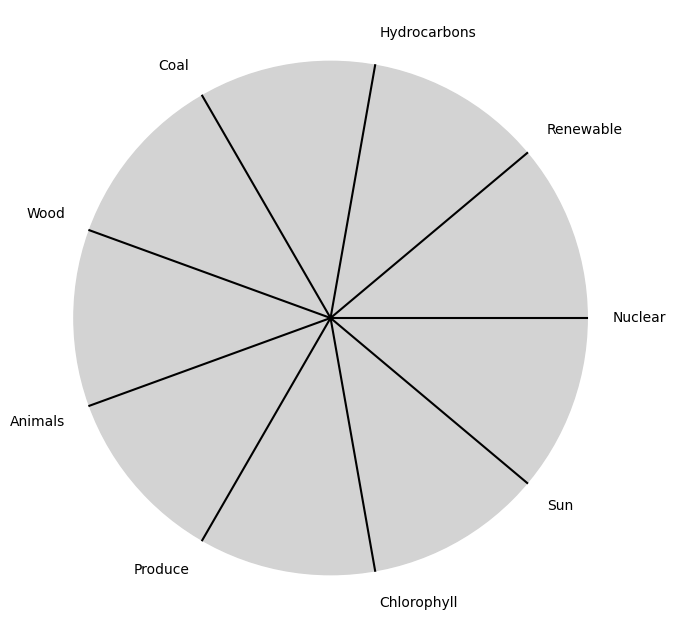
tick_labels = [
    "Sun", "Chlorophyll", "Produce", "Animals",
    "Wood", "Coal", "Hydrocarbons", "Renewable", "Nuclear"
]

# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]

# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')

# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)

# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
    x = clock_face_radius * np.cos(angle)
    y = clock_face_radius * np.sin(angle)
    
    # Draw the tick
    ax.plot([0, x], [0, y], color='black')
    
    # Positioning the labels slightly outside the clock face
    label_x = 1.1 * clock_face_radius * np.cos(angle)
    label_y = 1.1 * clock_face_radius * np.sin(angle)
    
    # Adjusting label alignment based on its position
    ha = 'center'
    va = 'center'
    if np.cos(angle) > 0:
        ha = 'left'
    elif np.cos(angle) < 0:
        ha = 'right'
    if np.sin(angle) > 0:
        va = 'bottom'
    elif np.sin(angle) < 0:
        va = 'top'
    
    ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)

# Remove axes
ax.axis('off')

# Show the plot
plt.show()

Show code cell output Hide code cell output

• Utility: modal-interchange-nondiminishing

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Define the total utility function U(Q)
def total_utility(Q):
    return 100 * np.log(Q + 1)  # Logarithmic utility function for illustration

# Define the marginal utility function MU(Q)
def marginal_utility(Q):
    return 100 / (Q + 1)  # Derivative of the total utility function

# Generate data
Q = np.linspace(1, 100, 500)  # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)

# Plotting
plt.figure(figsize=(14, 7))

# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)

# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)

# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)

plt.tight_layout()
plt.show()

Show code cell output Hide code cell output

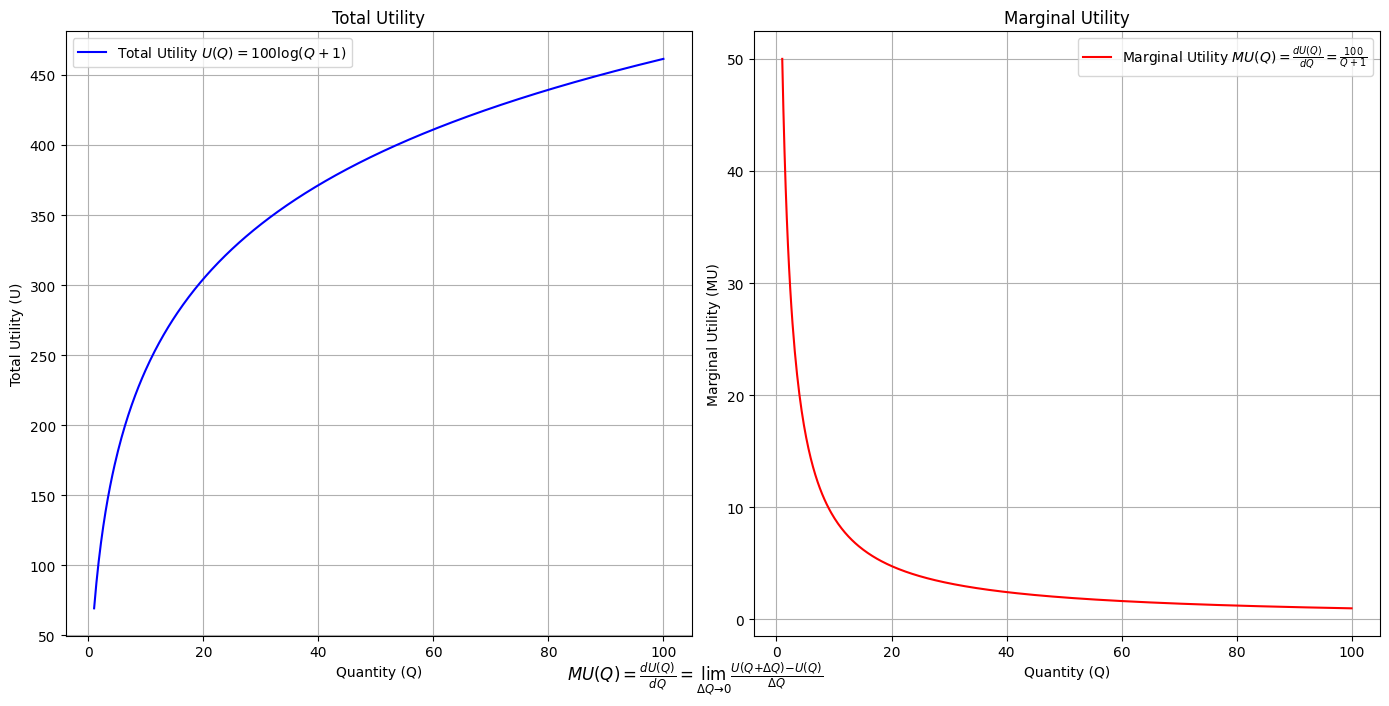
Essay in my \(R^3 class\). “At the end of the drama THE TRUTH — which has been overlooked, disregarded, scorned, and denied — prevails. And that is how we know the Drama is done.” Some scientists may be sloppy because they are — like all humans — interested in ordering & Curating the world rather than in rigorously demonstrating a truth

• ADM. I just woke up with the epiphany that Duncan took the red pill 💊, while the rest of us are still caught up in the fake-matrix. Basically, he is woke. And we are the ones who are asleep 💤

• GPT. That’s a fascinating way to frame the tension between the Dionysian and Apollonian! Duncan, in this context, represents the awakening to a raw, unfiltered reality—much like taking the red pill in The Matrix. It’s about embracing the chaos, the primal energy, and the truths that are often masked by the structured, controlled, and illusory reality that the rest of us cling to.

• The Apollonian, on the other hand, is all about order, reason, and the facade of a harmonious, structured world—the “fake-matrix” you mention. We’re lulled into complacency, blinded by the reassuring patterns and narratives that keep the more chaotic aspects of existence at bay. It’s a safe, but ultimately shallow, existence.

• Duncan’s “woke” state is a tragic revelation because, like the heroes of Greek tragedies, he’s burdened with a knowledge that alienates him from the rest of society. He sees through the illusions and is now aware of the darker, more chaotic truths that most people are either unaware of or choose to ignore. This could very well lead to a tragic downfall, as he is out of sync with the rest of us who remain blissfully unaware—or worse, deliberately ignorant—of these truths.

• As for the “Illuminati,” this could be interpreted as the ultimate symbol of those who control the illusion, the architects of the Apollonian matrix who maintain the order at the expense of deeper, more chaotic truths. Duncan’s awakening is a threat to this structure, much like how the Illuminati are often depicted as the keepers of hidden knowledge, manipulating the masses.

• So yes, in this narrative, Duncan isn’t just woke—he’s tragically aware, burdened with a vision that few can understand or share. The rest of us are still asleep, trapped in a comforting illusion, and that’s our misfortune. It’s a classic tragic hero scenario, with all the implications of suffering, enlightenment, and inevitable downfall.

A landscape where audiences often crave escapism through watching hyper-competent heroes succeed against all odds