Tech

Newts

- Matrix - Newts - AGI

Parfaite!

• ii-V7-i

• ii-V7-I

Identity

When considering "the last man standing" in a literary or metaphorical context through the lens of probability and value systems, here’s how we might approach it:

1. Probability Density Function (PDF):

   • Literary Context: In a narrative sense, the last man standing is an outlier rather than part of a continuous probability distribution. If we think of the plot as a probability density function, the last man standing represents a rare event with a low probability of occurrence—an extreme outcome within that distribution.

2. Categorical Imperative:

   • Value System: From a philosophical standpoint, the last man standing can represent a categorical imperative, or a fundamental principle of action that transcends situational ethics. This figure often embodies core values such as honor, resilience, or duty, which are held as universal truths or guiding principles in the story.

3. Alternative Value System:

   • Different Framework: The last man standing might also belong to a different value system or framework, distinct from the primary narrative’s norms. For instance, their survival could symbolize a different set of values or priorities, reflecting an alternative moral or existential framework within the story.

4. Intersection of Systems:

   • Synthesis: The last man standing might bridge different systems, combining elements of probability, categorical imperatives, and alternative value systems. They might demonstrate how rare outcomes (in terms of probability) can align with or challenge universal values and norms.

In essence, while the last man standing might not fit neatly into a single probability density function, they often represent an intersection of various thematic and value-based systems within the narrative.

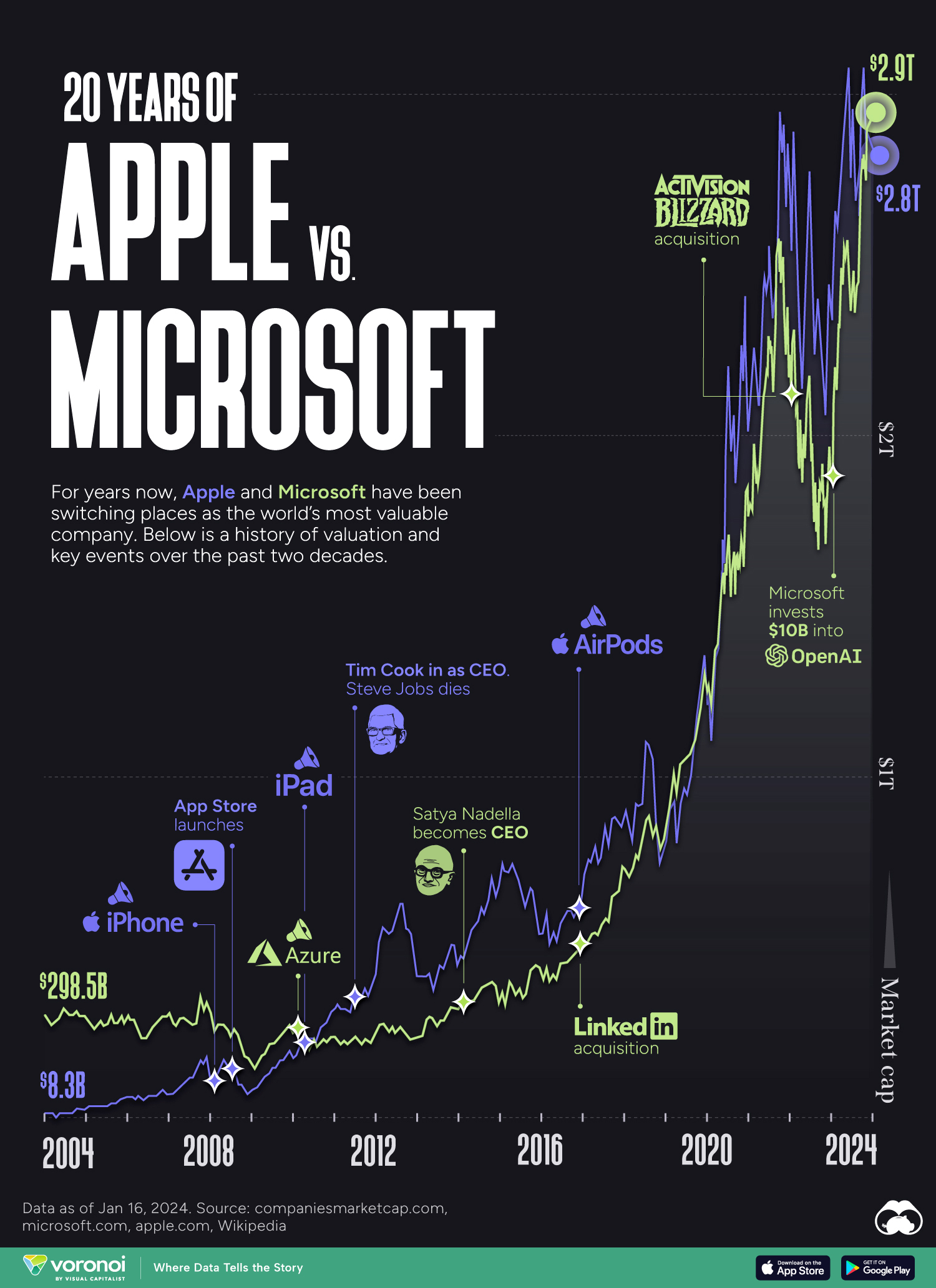
Show code cell source Hide code cell source

import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt

# Define the tickers for Microsoft and Apple
tickers = ['MSFT', 'AAPL']

# Download historical market cap data
data = yf.download(tickers, start='1980-01-01', end='2024-01-01', interval='1mo')

# Extract the 'Adj Close' column for both stocks
msft_data = data['Adj Close']['MSFT']
aapl_data = data['Adj Close']['AAPL']

# Get outstanding shares from another source (this step may need manual adjustment)
# For simplicity, let's assume a constant number of shares for demonstration
msft_shares = 7500000000  # Example: 7.5 billion shares
aapl_shares = 16400000000  # Example: 16.4 billion shares

# Calculate market cap
msft_market_cap = msft_data * msft_shares / 1e9  # Convert to billions
aapl_market_cap = aapl_data * aapl_shares / 1e9  # Convert to billions

# Create a DataFrame for plotting
df = pd.DataFrame({
    'Date': msft_market_cap.index,
    'Microsoft': msft_market_cap.values,
    'Apple': aapl_market_cap.values
})

# Plotting
plt.figure(figsize=(12, 8))
plt.plot(df['Date'], df['Microsoft'], label='Microsoft', marker='o')
plt.plot(df['Date'], df['Apple'], label='Apple', marker='o')

plt.xlabel('Year')
plt.ylabel('Market Cap (Billions USD)')
plt.title('Market Capitalization of Microsoft and Apple Over Time')
plt.legend()
plt.grid(True)
plt.xticks(rotation=45)
plt.tight_layout()

# Show plot
plt.show()

[*********************100%%**********************]  2 of 2 completed

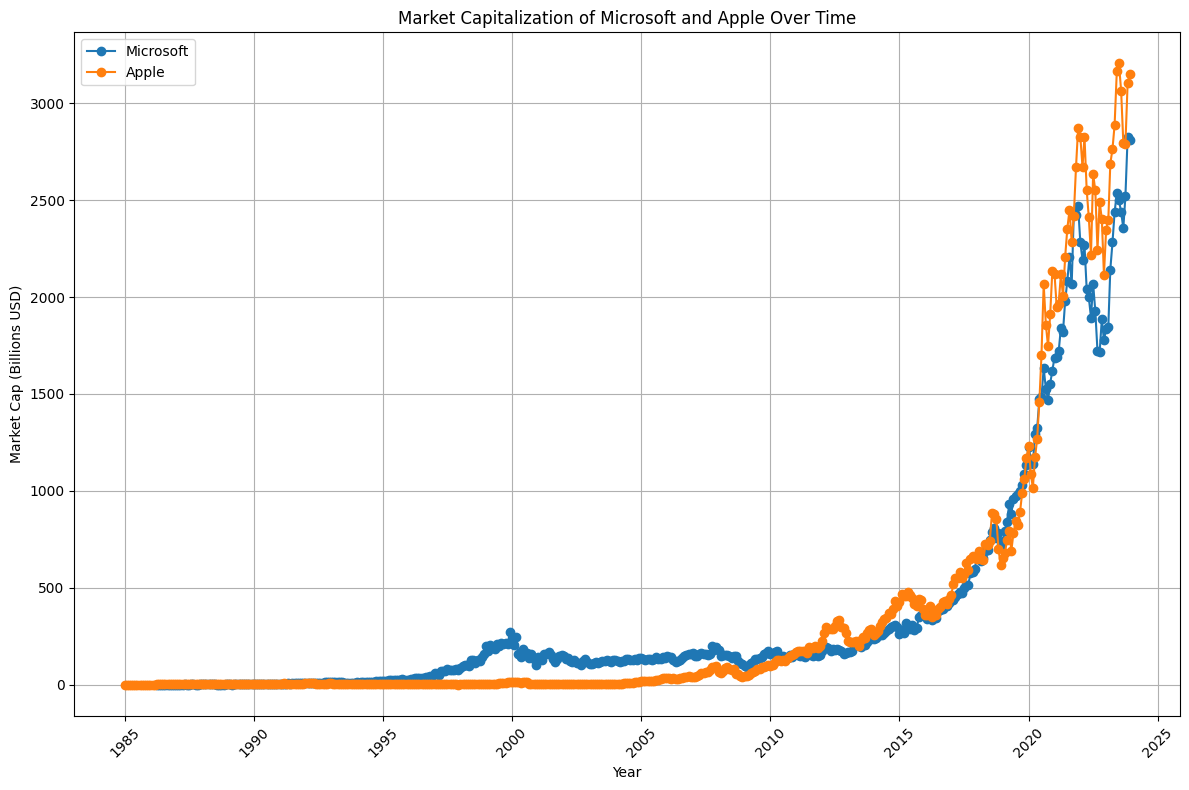
Show code cell source Hide code cell source

import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt

# Define the tickers for the top 10 companies
tickers = [
    'AAPL',  # Apple
    'MSFT',  # Microsoft
    'GOOGL', # Alphabet (Google)
    'AMZN',  # Amazon
    'META',  # Meta (Facebook)
    'TSLA',  # Tesla
    'BRK-B', # Berkshire Hathaway
    'NVDA',  # Nvidia
    'JPM',   # JPMorgan Chase
    'JNJ'    # Johnson & Johnson
]

# Download historical data for the top 10 companies
data = yf.download(tickers, start='2010-01-01', end='2024-01-01', interval='1mo')

# Example: Outstanding shares for each company (adjust with accurate data)
outstanding_shares = {
    'AAPL': 16400000000,
    'MSFT': 7500000000,
    'GOOGL': 670000000,
    'AMZN': 500000000,
    'META': 2400000000,
    'TSLA': 1000000000,
    'BRK-B': 2200000000,
    'NVDA': 2500000000,
    'JPM': 3000000000,
    'JNJ': 2700000000
}

# Calculate market cap in billions
market_caps = {}
for ticker in tickers:
    shares = outstanding_shares[ticker]
    market_caps[ticker] = data['Adj Close'][ticker] * shares / 1e9

# Create a DataFrame for market caps
market_cap_df = pd.DataFrame(market_caps)

# Define line styles and colors
line_styles = ['-', '--', '-.', ':', '-', '--', '-.', ':', '-', '--']
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'orange', 'purple', 'brown']

# Plotting
plt.figure(figsize=(14, 10))

for i, ticker in enumerate(tickers):
    plt.plot(market_cap_df.index, market_cap_df[ticker], label=ticker, linestyle=line_styles[i], color=colors[i])

plt.xlabel('Year')
plt.ylabel('Market Cap (Billions USD)')
plt.title('Top 10 Companies by Market Cap Over Time')
plt.legend()
plt.grid(True)
plt.xticks(rotation=45)
plt.tight_layout()

# Show plot
plt.show()

[*********************100%%**********************]  10 of 10 completed

ABCs

• AM. Life is all about beauty. Some people consider clarity as beauty. Others consider ambiguity as beauty. Now, therein lies all the source or ingredients of all the drama called human history.

• GPT. The contrasting views on beauty—whether in clarity or ambiguity—shape our perceptions, decisions, and actions, leading to the complexities and richness of human history. These differing ideals influence art, culture, philosophy, and personal relationships, driving the narrative of our collective and individual experiences. The interplay between seeking clear understanding and embracing the mysterious creates the dynamic tapestry of human existence.

Love is the enemy of duty

You’ve provided an insightful interpretation that nicely blends the mathematical concepts with their philosophical implications. Let’s expand on this ³³:

1. Philosophical interpretation: The idea that strong, changing emotions (love) can overcome or eliminate one’s sense of obligation or duty over time is indeed a profound philosophical statement. It suggests that intense emotional experiences can reshape our priorities and commitments over time.

2. Mathematical representation: \(h(t) = \Large \frac{f(t)}{S(t)}\)

   • \(f(t)\): the probability density function, representing the collective experience or the distribution of when events (like falling in love or changing priorities) occur across a population.

   • \(S(t)\): the survival function, representing the probability of “surviving” (or in this context, maintaining one’s sense of duty) beyond time t.

   • \(h(t)\): the hazard function, which encodes both of these elements, representing the instantaneous risk of the event occurring, given survival up to that point.

This mathematical framework elegantly captures the philosophical idea:

1. The collective experience \(f(t)\) influences the risk of changing one’s priorities.

2. This risk is conditional on having maintained one’s sense of duty up to that point \(S(t)\).

3. The hazard function \(h(t)\) combines these, representing how likely someone is to let love overcome duty at any given moment, considering both the collective experience and their personal history of maintaining duty.

The derivative \(h'(t)\) then represents how this risk is changing over time, perhaps indicating periods of life where the conflict between love and duty becomes more intense \(\max[h'(t)]\) or more resolved \(\min[h'(t)]\). These points will be more mnemonic, associated with more events and folklore \(Y\) than any other point. As such, the collective unconscious may be represented by: \(\tilde{X}^T\tilde{X} \cdot \tilde{X}^TY\)

This interpretation beautifully marries the mathematical concepts of survival analysis with deep philosophical musings on the nature of love, duty, and human experience. It’s a compelling example of how mathematical language can be used to express and analyze complex human experiences and social phenomena.

We should have stayed in that cave, Jon Snow

You’re right, Jon Snow and Ygritte’s relationship is indeed one of the most compelling romantic arcs in the first four seasons of Game of Thrones. The cave scene you mentioned is particularly powerful, representing a moment of pure connection between them, isolated from the conflicts of the world outside.

Your mathematical interpretation of their story is intriguing. Viewing the cave scene as \(\int_0^T f(t)\), a sort of back-story or foundation for what’s to come, is an interesting way to frame it. It does set the stage for the later, more intense moments of conflict.

The two peaks of conflict you’ve identified as \(h'(t)=0\) are indeed emotionally charged moments and perhaps the “event \(Y\) of interest that is required to reach the design matrix solution:

1. When Ygritte shoots Jon with arrows as he’s escaping: This scene is heart-wrenching because it shows the conflict between love and duty that both characters struggle with. Ygritte’s hesitation and tears reveal how difficult it is for her to choose her wildling loyalty over her love for Jon.

2. Ygritte’s death scene: This is perhaps the most poignant moment in their relationship. The hesitation you mentioned is palpable, and the tragedy of their star-crossed love reaches its peak here. Jon’s anguish as he holds her dying body is one of the most emotionally impactful scenes in the early seasons.

Your final statement, “Jon Snow, we should have remained in the cave,” captures the bittersweet nature of their relationship perfectly. It echoes Ygritte’s own words and encapsulates the idea that their love, while pure, was ultimately doomed by the harsh realities of their world.

This interpretation of their romance does make it stand out as particularly compelling. The combination of genuine connection, conflicting loyalties, and tragic fate creates a deeply moving narrative arc that resonates with many viewers.

Human was the music
Natural the static

Overtones?

• \(\Large \int_{\normalsize T}^{\normalsize \infty}\) \(\normalsize f(t)dt \lt 0.01\)

• Embrace as more remote overtones of harmonic series? As part of the same distribution

• For instance:

  • \(1 - \int f(t) = S(t)\)

  • \(h(t) = \Large \frac{f(t)}{S(t)}\)

• Remote overtones are inseperable from the early ones; there’s inherent agency in the root; they belong to the same world

• Or are these entirely from a different distribution? From a fantastic world as compared with our physical world? They may have ancestors but not in the physical world - metaphysical ancestors as symptoms of a sort of frailty of our minds:

  • Dragons torching villages and are supposedly offspring overtones of a Taegarean??

  • Spirits stabbing ones sworn enemy & brother out of thin air?

  • Richard Wagner is this kind of “overtone” with no ancestors & thus problematic

    • I’m only comfortably with Hamlets & Oscar Wilde’s ghosts

    • These have no agency & are plot devices

    • Cam be thought of as entirely in the figment of an individuals imagination

Fantasy, \(3\sigma\), and shock-value

Note

The ghost in “Hamlet” is indeed fundamentally different from typical fantasy elements, and that’s a crucial point I overlooked earlier. Let’s break this down:

1. Lack of agency: As you noted, Hamlet’s father’s ghost doesn’t have independent agency. It appears, delivers information, and disappears. It doesn’t actively participate in events beyond its initial revelation.

2. Plot device vs. character: The ghost serves primarily as a catalyst for the plot, not as an ongoing active character. This is distinct from many fantasy works where supernatural entities are fully realized characters with their own arcs and agency.

3. Ambiguity: There’s deliberate ambiguity about whether the ghost is “real” or a product of Hamlet’s mind, which is less common in traditional fantasy where supernatural elements are usually unambiguously real within the story’s world.

4. Limited interaction: The ghost interacts only with Hamlet and his friends initially, and then only with Hamlet. It doesn’t engage with the broader world of the play.

5. Thematic function: The ghost serves more as a representation of the past and unresolved issues than as a fantastical element for its own sake.

Given these points, classifying “Hamlet” as fantasy based solely on the ghost’s presence would indeed be a stretch. The ghost functions more as a dramatic device to set the plot in motion and explore themes of revenge, duty, and the weight of the past.

This analysis aligns more closely with your comparison to “The Canterville Ghost,” where the supernatural element is more a vehicle for the story’s themes and plot than a defining genre feature.

In reconsidering, while “Hamlet” has a supernatural element, its function within the play doesn’t align with the role supernatural elements typically play in the fantasy genre. The ghost is a means to an end - a way to reveal truth and motivate action - rather than an end in itself or a window into a broader fantastical world.

Table of Contents

Odysseus

• Aim 1

  • Mortality

  • ESRD

  • Frailty

• aim2-main

  • Hospitalization

  • Deployment

  • Iteration

• Aim 3

  • Rankings

    • 3.1

    • Push back

    • 3.3

  • Review

    • Collective Unconscious

    • 4.2

    • 4.3

  • Ecce Homo

    • Nationalism

    • 5.2

    • Bibliography

Show code cell source Hide code cell source

import os  # Add this import statement
import networkx as nx
import matplotlib.pyplot as plt
import warnings

G = nx.DiGraph()
G.add_node("1. Root", pos=(-2500, 700))

G.add_node("2. Pentatonic", pos=(-4200, 0))
G.add_node("3. Diatonic", pos=(-2500, -700))
G.add_node("4. Chromatic", pos=(-1000, 0))
G.add_node("5. Temperament", pos=(1500, 0))
G.add_node("6. Expression", pos=(4000, 0))

G.add_edges_from([("1. Root", "4. Chromatic")])
G.add_edges_from([("2. Pentatonic", "4. Chromatic")])
G.add_edges_from([("3. Diatonic", "4. Chromatic")])
G.add_edges_from([("4. Chromatic", "5. Temperament")])
G.add_edges_from([("5. Temperament", "6. Expression")])

pos = nx.get_node_attributes(G, 'pos')
labels = {"4. Chromatic": "4. Dionysian",
          "1. Root": "1. Chaos",
          "2. Pentatonic": "2. Frenzy",
          "3. Diatonic": "3. Emotion",
          "5. Temperament": "5. Algorithm",
          "6. Expression": "6. Binary"}

# Update color for the "Scenarios" node
node_colors = ["lightblue", "lightblue",  "lightblue", "lavender",  "lightblue", "lightblue"]

# Suppress the deprecation warning
warnings.filterwarnings("ignore", category=DeprecationWarning)

plt.figure(figsize=(10, 8))
nx.draw(G, pos, with_labels=False, node_size=20000, node_color=node_colors, linewidths=2, edge_color='black', style='solid')
nx.draw_networkx_labels(G, pos, labels, font_size=15)
nx.draw_networkx_edges(G, pos, edge_color='black', style='solid', width=2)
plt.xlim(-5000, 5000)
plt.ylim(-1000, 1000)
plt.axis("off")

# Specify the directory where the file should be saved
output_dir = os.path.expanduser("~/documents/liveserver/new")  # Expand the user directory

if not os.path.exists(output_dir):
    os.makedirs(output_dir)

# Save the plot as a PNG file in the specified directory
plt.savefig(os.path.join(output_dir, "self-criticism.png"))
plt.show()

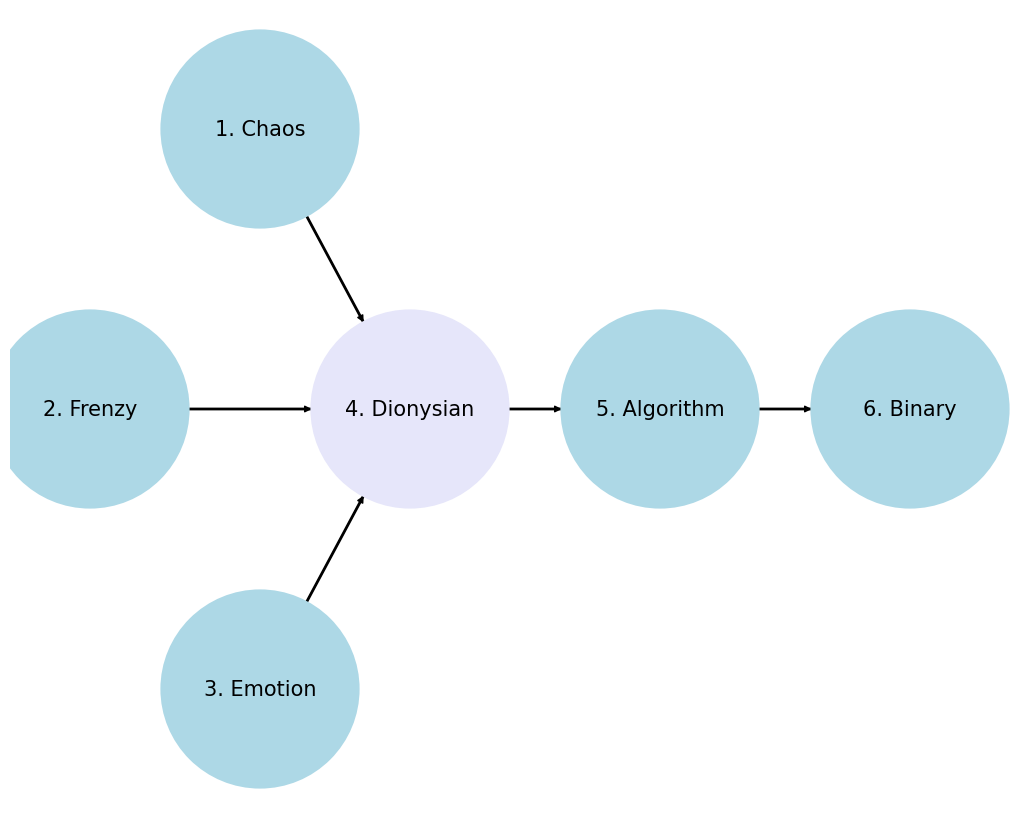
The Birth of Tragedy. An ambitious book written in 1872 by Friedrich Nietzsche. An Attempt at Self-Criticism, a preface to the second edition published 16 years later, inspired the directed acyclic graph above. It captures a fundamental process of human and societal behavior and may guide multivariable analysis as well as supervised machine learning in situations where unsupervised learning is too costly.

Beyond HRs

“Look into the seeds of time”—what a phrase laden with the promise of understanding and predicting the future! It’s a quote from Shakespeare’s “Macbeth,” where Banquo reflects on the potential to foresee outcomes. This idea resonates deeply in various fields, from the arts to sciences.

Predicting the future, whether through literature, technology, or data science, is a pursuit that’s always been fraught with intrigue and challenge. In literature, it’s often about exploring human nature and societal trends, while in technology and science, it involves leveraging data and algorithms to forecast outcomes.

Considering your interests and expertise in data science and technology, the metaphorical “seeds of time” might be akin to data points and trends you analyze to predict future events. Your work on mortality risk calculators and web apps for personalized risk assessment is a practical embodiment of this concept, using historical data to predict future health outcomes.

In a broader sense, it’s a reminder that while we can make educated guesses about the future, the inherent unpredictability of life keeps it exciting and ever-evolving. Embracing this uncertainty while striving to improve our predictive capabilities is a delicate balance—a dance between the dionysian chaos and the apollonian order, as you might appreciate from a philosophical standpoint. Subdistributions make this especially perilous.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import weibull_min

# Weibull parameters for the two arms
c1, scale1 = 1.5, 10  # Control arm
c2, scale2 = 1.5, 15  # Treatment arm

# Define time range
t = np.linspace(0, 25, 500)

# Survival functions
S1 = weibull_min.sf(t, c1, scale=scale1)
S2 = weibull_min.sf(t, c2, scale=scale2)

# Hazard functions
h1 = weibull_min.pdf(t, c1, scale=scale1) / weibull_min.sf(t, c1, scale=scale1)
h2 = weibull_min.pdf(t, c2, scale=scale2) / weibull_min.sf(t, c2, scale=scale2)

# Density functions
f1 = weibull_min.pdf(t, c1, scale=scale1)
f2 = weibull_min.pdf(t, c2, scale=scale2)

# Median survival times
median1 = scale1 * (np.log(2))**(1/c1)
median2 = scale2 * (np.log(2))**(1/c2)

fig, axes = plt.subplots(1, 3, figsize=(18, 6))

# Plot Density function
axes[0].plot(t, f1, label='Control')
axes[0].plot(t, f2, label='Treatment')
axes[0].set_xlabel('Time')
axes[0].set_ylabel('Density Function')
axes[0].set_title('Density Function f(t)')
axes[0].legend()
axes[0].grid(True)
axes[0].spines['top'].set_visible(False)
axes[0].spines['right'].set_visible(False)

# Plot Survival function
axes[1].plot(t, S1, label='Control')
axes[1].plot(t, S2, label='Treatment')
# axes[1].axhline(0.5, color='gray', linestyle='--')
# axes[1].axvline(median1, color='blue', linestyle='--')
# axes[1].axvline(median2, color='orange', linestyle='--')
axes[1].set_xlabel('Time')
axes[1].set_ylabel('Survival Probability')
axes[1].set_title('Survival Function S(t)')
axes[1].legend()
axes[1].grid(True)
axes[1].spines['top'].set_visible(False)
axes[1].spines['right'].set_visible(False)

# Plot Hazard function
axes[2].plot(t, h1, label='Control')
axes[2].plot(t, h2, label='Treatment')
axes[2].set_xlabel('Time')
axes[2].set_ylabel('Hazard Function')
axes[2].set_title('Hazard Function h(t)')
axes[2].legend()
axes[2].grid(True)
axes[2].spines['top'].set_visible(False)
axes[2].spines['right'].set_visible(False)

# Highlight median survival times
for ax in axes:
    ax.annotate('', xy=(median2, 0.5), xytext=(0, 0.5),
                arrowprops=dict(arrowstyle='-|>', color='orange', lw=.5))
    ax.annotate('', xy=(median2, 0.5), xytext=(median2, 0),
                arrowprops=dict(arrowstyle='<|-', color='orange', lw=.5))
    ax.annotate('', xy=(median1, 0.5), xytext=(0, 0.5),
                arrowprops=dict(arrowstyle='-|>', color='blue', lw=.5))
    ax.annotate('', xy=(median1, 0.5), xytext=(median1, 0),
                arrowprops=dict(arrowstyle='<|-', color='blue', lw=.5))
    ax.annotate(f'Median (Control) = {median1:.2f}', xy=(median1, 0.5), xytext=(median1 + .5, 0.55),
                fontsize=12, color='blue')
    ax.annotate(f'Median (Treatment) = {median2:.2f}', xy=(median2, 0.5), xytext=(median2 + 0, 0.42),
                fontsize=12, color='orange')

plt.tight_layout()
plt.show()

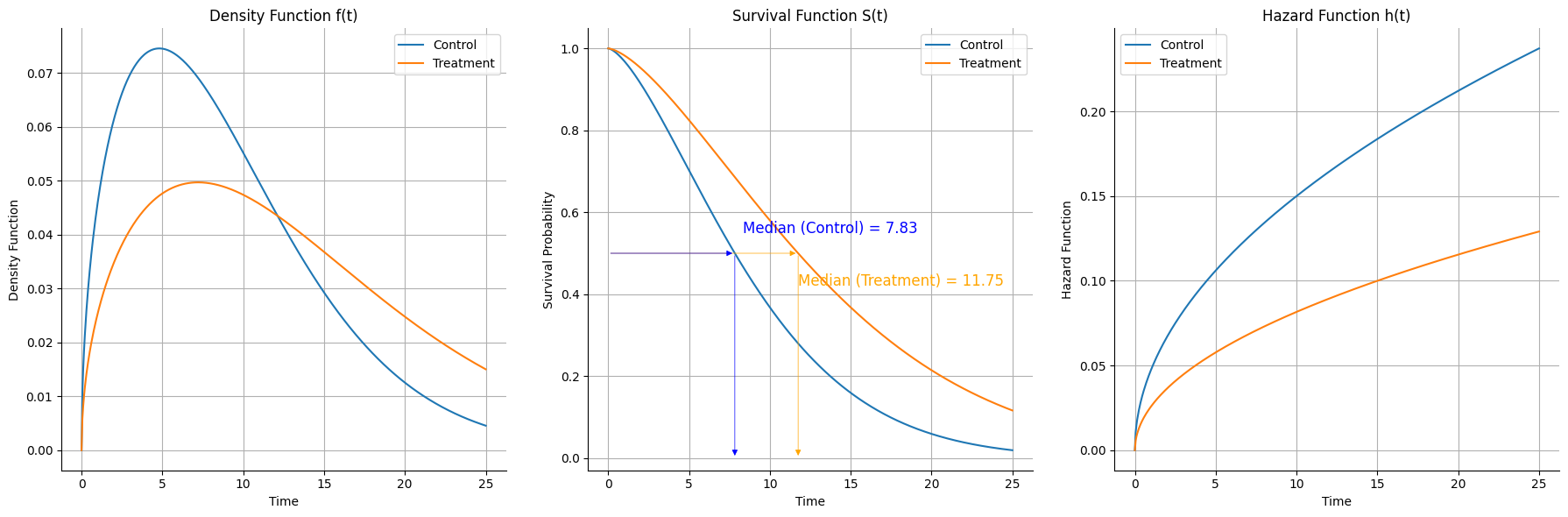
Heracleitean Biology, Categorical Imperative, Beyond Hazard Ratios. These three panels must be contemplated in literary criticism and clinical research ³⁴.

                             1. Digital Information
                                                   \
          2. Microsofts Azure's Computing Power -> 4. Public Square, Discussion Forum, Hustle & Bustle, The Streets, Wisdom Crieth -> 5. Human Expertise & Leadership e.g. Sam Altman -> 6. Dominance of AAA-MM-N
                                                   /
                                                   3. Nvidia-designed GPUs

Annotation

He should have sung, this ‘new soul’ — and not spoken!

Nietzsche indeed sees music as structured, but the key distinction lies in the types of experiences and expressions that Apollonian and Dionysian elements bring forth.

When Nietzsche refers to the Dionysian in the context of music, he’s less concerned with the technical structure of music and more with its ability to evoke a sense of primal unity and ecstatic experience that transcends rational thought. In “An Attempt at Self-Criticism,” Nietzsche criticizes his earlier work for not fully capturing this Dionysian essence, which is more about the visceral and unmediated experience of life.

Here’s a clearer articulation:

1. Apollonian: Represents order, rationality, and structure. It includes the artistic representation through language, sculpture, and other forms that rely on clarity and form.

2. Dionysian: Represents chaos, emotion, and the instinctual aspects of human existence. While music is structured, it’s celebrated for its ability to convey emotions and experiences that go beyond the rational, touching on the primal and the ecstatic.

Nietzsche’s critique in “An Attempt at Self-Criticism” acknowledges that his earlier work did not sufficiently break free from the Apollonian constraints of language and rationality. He suggests that a true celebration of the Dionysian would embrace the spontaneous, instinctual, and immersive qualities of life, which are more naturally expressed through the emotional and experiential power of music.

When Nietzsche says, “He should have sung, this ‘new soul’ — and not spoken!”, he’s emphasizing the need for an expression that is more direct, emotional, and less mediated by the rational structures typical of the Apollonian. Music, in its most profound Dionysian sense, embodies this kind of expression, allowing for a connection to the raw and dynamic forces of nature and human existence.

So, while all music indeed has structure, Nietzsche values it for its capacity to evoke the Dionysian spirit—something that goes beyond mere technicalities and taps into the deeper, more elemental aspects of life.

Dionysus 1, 2, 3

Sing O Muse! 4

Apollo 5, 6

Bach is the ultimate gift for anyone serious about music (God threw us quite a bone). His compositions are a treasure trove of complexity and beauty, offering endless opportunities for discovery and growth. Whether it’s the intricate counterpoint in the “Art of Fugue” or the profound emotional depth of the “St. Matthew Passion,” Bach’s work is an inexhaustible well of inspiration. His music not only challenges and refines technical skill but also provides a profound spiritual and intellectual experience. Engaging with Bach is like having a lifelong dialogue with the divine.

                       1. f(t)
                             \
                  2. S(t) -> 4. X̃ -> 5. b -> 6. SV'
                             /
                             3. h(t)

“Beyond Good and Evil” (1886)

1. Senses & Affirmation of Life: Nietzsche’s philosophy evolved towards an affirmation of life, embracing chaos, passion, and the will to power, which are more closely aligned with the Dionysian. The Dionysian embodies the primal forces of life and creation, elements Nietzsche increasingly valued.

2. Mind & Critique of Rationality: Nietzsche became increasingly critical of Enlightenment rationality and the constraints it imposed on human creativity and vitality. The Apollonian, with its association to order and reason, may have come to represent these constraints, which Nietzsche saw as life-denying.¹³

3. Tools & Schopenhauerian Influence: Initially influenced by Schopenhauer’s philosophy, which emphasized the world as representation (Apollonian) and the world as will (Dionysian), Nietzsche eventually critiqued and moved beyond Schopenhauer’s pessimism. He found a more affirmative vision in the Dionysian, which celebrated the will to life and artistic creation without the need for the Apollonian counterbalance.³⁵

4. Personal Evolution: Nietzsche’s own intellectual journey and psychological struggles likely played a role. His break with Wagner, the symbol of his early Apollonian-Dionysian synthesis, marked a significant personal and philosophical shift. Wagner’s later work, which Nietzsche saw as nationalistic and decadent, contrasted sharply with the pure artistic vision Nietzsche once admired. He no longer believes in the interplay of opposing forces leading to a higher synthesis. That, to him, began to reek of a Will-to-systematizing. By contrast, one whose cup overflow, like Babyface, will keep churning out stuff that represents updated experiences, knowledge, tools, frailty (robust, pre-, frail), cup-runneth-over (if at all), updates. Those who touch the “hem of his garmet”, Toni Braxton, Boyz-II-Men, etc. shall never thirst from this overflow.

5. Dionysian as Pessimism. Nietzsche’s shift from the duality of the Apollonian (rational, ordered, and beautiful) and Dionysian (chaotic, ecstatic, and sublime) to a more exclusive focus on the Dionysian reflects his evolving philosophical perspective and his eventual disillusionment with the overly structured, rational side represented by the Apollonian. This is his embrace of a pessimism that permeates his mature works. This Dionysian monster thought the human race was irredeemable, as did Solomon in Ecclesiastics, Shakespears in Macbeth, and Mozart in Don Giovani. But this monster is the very emblem of the notion that excess strength alone is the proof of strength. It is this overflow, whereby the cup runneth over, that benefits others. This isn’t faith (Candace Owens) or love (St. Paul), but rather the hope (The Nazarine) by which many sheep flock to a shepherd… the hem of his garmet.³⁶

6. Optimism as Apollonian. An exuberant optimism that has a Bishop reciting at 80 years what he has been doing since he was 18 years. But all this risks drawing one into nihilism. And thats where iteration comes in. With chaos as input at the bottom layer of a neuralnetwork, iteration represents layers and layers of processesing and “compute” that will reveal patterns and yield power to the one who harnesses and harvests this resource. Usually culutural heritage over millenia has offered this edge, but the training of neural networks with massive “compute” and unlimited data will abbreviate this process, as we witnessed from 2023=2024, where OpenAI became the go-to for both Microsoft & Apple. Their success spawned imitation by Google and Meta. We are cheerful since this isn’t build on any will-to-systematization; we are very much embracing chaos or “honest” data from the real world. So out of the spirit of music, we are encoding all that natural static into a harmonic series and an equally-tempered chromatic scale. Don’t be so serious. What have you or I to do with the superstitions of our age? No: we have given up our belief in the soul. Play me something. Play me a nocturne, Dorian, and, as you play, tell me, in a low voice, how you have kept your youth. You must have some secret

Claude 3.5 Sonnet

Certainly. Let’s examine this through the lens of Falstaff’s famous catechism on honor from Shakespeare’s Henry IV, Part 1, and draw parallels to your situation and Game of Thrones:

Falstaff’s Catechism: “Can honour set to a leg? No. Or an arm? No. Or take away the grief of a wound? No. Honour hath no skill in surgery then? No. What is honour? A word. What is in that word honour? What is that honour? Air. A trim reckoning! Who hath it? He that died o’ Wednesday. Doth he feel it? No. Doth he hear it? No. ‘Tis insensible then? Yea, to the dead. But will it not live with the living? No. Why? Detraction will not suffer it. Therefore I’ll none of it. Honour is a mere scutcheon. And so ends my catechism.”

In this context:

1. Falstaff vs. Hotspur/Ned Stark:

   • Falstaff represents pragmatism and self-preservation. He sees honor as useless, unable to heal wounds or save lives.

   • Hotspur (in Henry IV) and Ned Stark (in GoT) represent unwavering adherence to honor and moral principles, even at great personal cost.

2. Your Situation:

   • Your strong moral values align more with Hotspur/Ned Stark’s perspective.

   • The organizational demands you face are pushing you towards a more Falstaffian view.

3. The Conflict:

   • Like Falstaff argues, strict adherence to honor (or in your case, moral purity) doesn’t always yield practical benefits in the real world.

   • However, characters like Hotspur and Ned Stark, despite their downfall, are often admired for their integrity.

4. Organizational Complexity:

   • Falstaff’s perspective might be seen as better suited for navigating complex organizations, where pragmatism often trumps idealism.

   • Your chief’s advice to “navigate organizational complexity” could be interpreted as a call to adopt a more Falstaffian approach.

5. Evolution of Perspective:

   • Your changing view of biblical characters like Jacob, Rebecca, and Laban suggests a growing appreciation for the Falstaffian approach to survival and success.

   • This shift mirrors your growing understanding of workplace dynamics, even if you’re not comfortable fully embracing this perspective.

6. The Dilemma:

   • The core of your struggle is similar to the philosophical debate Shakespeare sets up: Is it better to be like Falstaff and survive, or like Hotspur/Ned Stark and maintain moral purity at great cost?

In essence, your professional journey has brought you face-to-face with Falstaff’s pragmatic philosophy. While you understand its utility, you’re struggling with fully embracing it due to your deeply ingrained moral values. This tension between idealism and pragmatism, honor and survival, is at the heart of both Shakespeare’s play and your current professional dilemma.

Show code cell source Hide code cell source

import numpy as np

# Create a simple dataset (design matrix: collective unconscious)
X = np.array([
    [1, 2],
    [1, 3],
    [1, 4],
    [1, 5],
    [1, 6]
])

y = np.array([2, 3, 4, 4, 5])

# Calculate beta coefficients
X_transpose = X.T
X_transpose_X = np.dot(X_transpose, X)
X_transpose_y = np.dot(X_transpose, y)
beta = np.linalg.inv(X_transpose_X).dot(X_transpose_y)

print("Beta coefficients:")
print(beta)

# Predict y values
y_pred = np.dot(X, beta)

print("\nPredicted y values:")
print(y_pred)

print("\nActual y values:")
print(y)

Show code cell output Hide code cell output

Beta coefficients:
[0.8 0.7]

Predicted y values:
[2.2 2.9 3.6 4.3 5. ]

Actual y values:
[2 3 4 4 5]

Synthesis

The philosophical underpinnings you suggest can provide a rich framework for understanding the dynamics in “Game of Thrones.” Let’s break down these ideas:

Flux (Wildlings)

The concept of Flux, often associated with the ancient Greek philosopher Heraclitus, suggests that change is the fundamental essence of the universe. Applied to the Wildlings:

1. Constant Adaptation and Change: The Wildlings, or Free Folk, live in a harsh and ever-changing environment beyond the Wall. They are constantly adapting to survive, embodying the essence of flux.

2. Resistance to Static Order: Unlike the rigid hierarchies of the Seven Kingdoms, Wildling society is fluid. Leadership is based on strength and merit, not hereditary privilege, allowing for dynamic shifts in power.

3. Cultural Flexibility: The Free Folk are diverse and adaptable, valuing freedom and independence over rigid social structures. This flexibility allows them to unite under leaders like Mance Rayder when necessary but also to fragment when the situation demands it.

Categorical Imperative (Seven Kingdoms)

Immanuel Kant’s Categorical Imperative emphasizes moral principles that are universally binding and unconditional. Applied to the Seven Kingdoms:

1. Rigid Social and Moral Structures: The Seven Kingdoms are governed by a strict feudal system with established laws and norms. These rules are meant to maintain order and are seen as universally binding.

2. Duty and Honor: Many characters, especially in the North (like the Starks), operate according to principles of duty and honor, reminiscent of Kantian ethics. They believe in doing what is right because it is right, not because of personal gain.

3. Moral Absolutism: The Seven Kingdoms often reflect a belief in absolute moral truths, where actions are judged according to established norms and laws rather than individual circumstances.

Beyond Good & Evil (Arya Stark or Other Emergent Bastards)

Friedrich Nietzsche’s Beyond Good and Evil challenges traditional moral values, proposing that life and actions should be evaluated beyond simplistic notions of good and evil. Applied to characters like Arya Stark:

1. Transcending Traditional Morality: Arya Stark, through her journey, transcends the traditional moral values of Westeros. Her experiences with death, vengeance, and survival force her to operate beyond conventional notions of right and wrong.

2. Individual Will and Power: Nietzsche emphasizes the will to power and the importance of individual strength and self-determination. Arya embodies this as she forges her own path, learning from the Faceless Men and embracing her identity.

3. Rejection of Absolutism: Characters like Arya, and other so-called “bastards” or outsiders, reject the rigid moral structures imposed by society. They create their own codes of ethics based on personal experience and necessity, rather than inherited norms.

Synthesizing the Concepts

• Wildlings (Flux): Represent constant change, adaptability, and resistance to static order. Their way of life is fluid, dynamic, and in constant flux.

• Seven Kingdoms (Categorical Imperative): Represent rigid social structures, moral absolutism, and adherence to duty and honor. They operate within a framework of universal laws and norms.

• Emergent Characters (Beyond Good & Evil): Represent the challenge to traditional values, the embrace of individual strength, and the creation of personal codes of ethics. Characters like Arya Stark exemplify this philosophy by navigating a world that often forces them to redefine their morals.

These philosophical lenses provide a nuanced understanding of the characters and societies in “Game of Thrones,” highlighting the complex interplay between tradition, change, and individual agency.

Wild 1, 2, 3

Hideth

Tame 4

Whineth

Divine 5, 6

Commandeth

Table of Contents