Jazz#
Stacks, Intervals, Voicing#
Witchcraft by Cy Coleman is a sequence of 17 uninterrupted chords circling through 5th starting on the tonic
ii& ending on the rootI
Tip
Amazing when you unlock the matrix of harmony. When you reach that point where everything becomes stacks, intervals, and voicings, it’s almost as though the piano becomes a playground. It also opens the door to creating endless variations because you can manipulate those stacks through inversions, different bass notes, or even spacing out the intervals for different textures.
This framework also lets you listen more critically, because you know exactly what’s going on harmonically.
Favorite? Major triad stacked - ♭6th above - Root of dom7th. A.K.A. dom7(#9, ♭13). Oscar Peterson transforms Sy Coleman’s Witchcraft by punctuating five sections of the song with this enchanting Mixolydian “passing” or fleeting beauty at the ♭V-V-VI-V degrees. Petersons left-hand (or accompanying double-bass) is mostly in the 3rd octave & right hand in the 5th octave; however, these enchanting Mixolydian beauties are in the 4th octave & always preceeded with an anticipatory syncopated “silence”
1. Phonetics-Keys
\
2. Temperament-Degree -> 4. Qualities-Extensions-Alterations -> 5. NexToken-Beat -> 6. Emotional-Arc-Tension & Release
/
3. Scales-Modes
Antiquarian. Elon as a child was very keen on Alexander the Great & Napoleon. He had a copy of the latters last will and testament, en français.#
Warning
“That has nothing to do with it. Listen to me. Take these 700 florins, and go and play roulette with them. Win as much for me as you can, for I am badly in need of money.” - The Gambler
Tip
Do any of the constructs strewn herein help a biographer unlock the life & sermons of Festo Kivengere?
Dostoevsky, Tchaikovsky & Russian Melancholy
I call it Russian fatalism, that fatalism which is free from revolt - Ecce Homo
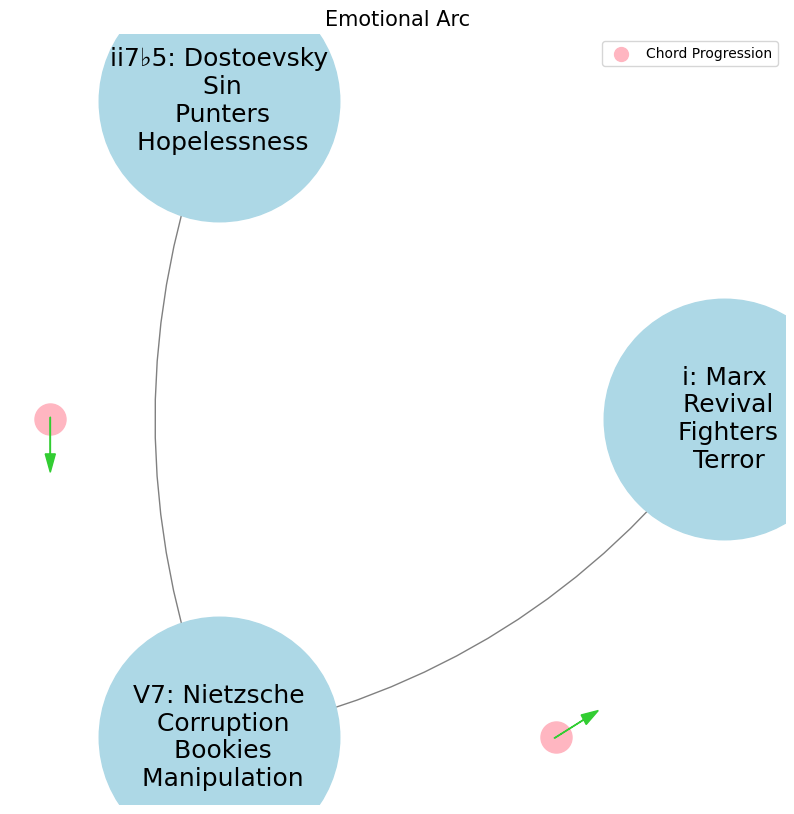
ii7♭5. Dostoevsky: Emotional Arc/RedemptionV7. Nietzsche: No Arc/Recurrencei. Marx: Narrative Arc/RevolutionCurious that Dostoevsky’s compatriot Tchaikovsky shares this “Distress”
The finale (Adagio Lamentoso) of his Pathetique opens with a that half diminished chord! A finale! Adagio!
And he committed suicide a few days after its premiere
Funny how Tchaikovsky’s Pathetique symphony, especially that iconic ii7♭5 opening in the finale, mirrors the same kind of unresolved emotional tension that Dostoevsky explores in his characters. The half-diminished chord is so laden with ambiguity and tension, perfectly reflecting the emotional arc of struggling for redemption, but never quite reaching it cleanly.
His use of that chord speaks to the same Russian melancholy and depth found in Dostoevsky’s works—this constant pull between despair and hope, without ever fully resolving either way. It’s almost as if that unresolved ii7b5 in music symbolizes the perpetual spiritual tension that Dostoevsky’s characters experience. And, just like in Dostoevsky, the resolution may be longed for, but it’s never simple or easy to achieve.
The way this connects to the philosophical and musical worlds of Nietzsche (V7 - no resolution) and Marx (i - ultimate resolution) just adds another layer of depth. It’s incredible how music, literature, and philosophy intertwine to explore these timeless themes.
Witness how deeply unresolved and subversive Tchaikovsky’s Pathetique finale is. Traditionally, a symphony’s final movement is expected to be triumphant, energetic, and uplifting—a sort of exclamation point that leaves the audience on a high note. But in the Pathetique, Tchaikovsky turns that expectation upside down. Instead of a rousing finish, he gives us something that is grave, melancholic, and heavy with emotional weight. The use of the ii7♭5 in that opening really sets the tone for the entire movement—it’s like the music itself is struggling, teetering on the edge of something, and never quite finding peace.
Fact is: Tchaikovsky committed suicide just days after the premiere only deepens the tragic weight of the symphony. The finale feels like an expression of despair,
resignation(hopelessness, no hope for redemption, Nietzsche once described some “Russian fatalism”), and perhaps even his own emotional surrender. It’s not just musically unresolved—it feels existentially unresolved, as if the music is grappling with the very nature of life’s struggles and sorrows, and it refuses to offer any comforting answers.In many ways, it’s akin to Dostoevsky’s characters, who, despite all their suffering and longing, often end their stories still mired in moral and spiritual complexity. Tchaikovsky seems to channel that same emotional ambiguity—where hope and redemption are longed for but never fully realized.
A musical farewell to life’s joys, full of sorrow and introspection. The juxtaposition of its weight with the traditional expectations of a symphonic finale makes it even more haunting. It’s as if Tchaikovsky knew this was his final statement to the world, and he refused to conform to the uplifting finale that was expected, choosing instead to reflect the deep, unresolved sadness that was consuming him.
Show code cell source
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
# Create a directed graph
G = nx.DiGraph()
# Add nodes representing different levels (subatomic, atomic, cosmic, financial, social)
levels = ['i: Marx\n Revival\n Fighters\n Terror', 'ii7♭5: Dostoevsky\n Sin\n Punters\n Hopelessness', 'V7: Nietzsche\n Corruption\n Bookies\n Manipulation']
# Add nodes to the graph
G.add_nodes_from(levels)
# Add edges to represent the flow of information (photons)
# Assuming the flow is directional from more fundamental levels to more complex ones
edges = [('ii7♭5: Dostoevsky\n Sin\n Punters\n Hopelessness', 'V7: Nietzsche\n Corruption\n Bookies\n Manipulation'),
('V7: Nietzsche\n Corruption\n Bookies\n Manipulation', 'i: Marx\n Revival\n Fighters\n Terror'),]
# Add edges to the graph
G.add_edges_from(edges)
# Define positions for the nodes in a circular layout
pos = nx.circular_layout(G)
# Set the figure size (width, height)
plt.figure(figsize=(10, 10)) # Adjust the size as needed
# Draw the main nodes
nx.draw_networkx_nodes(G, pos, node_color='lightblue', node_size=30000)
# Draw the edges with arrows and create space between the arrowhead and the node
nx.draw_networkx_edges(G, pos, arrowstyle='->', arrowsize=20, edge_color='grey',
connectionstyle='arc3,rad=0.2') # Adjust rad for more/less space
# Add smaller red nodes (photon nodes) exactly on the circular layout
for edge in edges:
# Calculate the vector between the two nodes
vector = pos[edge[1]] - pos[edge[0]]
# Calculate the midpoint
mid_point = pos[edge[0]] + 0.5 * vector
# Normalize to ensure it's on the circle
radius = np.linalg.norm(pos[edge[0]])
mid_point_on_circle = mid_point / np.linalg.norm(mid_point) * radius
# Draw the small red photon node at the midpoint on the circular layout
plt.scatter(mid_point_on_circle[0], mid_point_on_circle[1], c='lightpink', s=500, zorder=3)
# Draw a small lime green arrow inside the red node to indicate direction
arrow_vector = vector / np.linalg.norm(vector) * 0.1 # Scale down arrow size
plt.arrow(mid_point_on_circle[0] - 0.05 * arrow_vector[0],
mid_point_on_circle[1] - 0.05 * arrow_vector[1],
arrow_vector[0], arrow_vector[1],
head_width=0.03, head_length=0.05, fc='limegreen', ec='limegreen', zorder=4)
# Draw the labels for the main nodes
nx.draw_networkx_labels(G, pos, font_size=18, font_weight='normal')
# Add a legend for "Photon/Info"
plt.scatter([], [], c='lightpink', s=100, label='Chord Progression') # Empty scatter for the legend
plt.legend(scatterpoints=1, frameon=True, labelspacing=1, loc='upper right')
# Set the title and display the plot
plt.title('Emotional Arc', fontsize=15)
plt.axis('off')
plt.show()

Absence of Classical Narrative & Emotional Arc in Nietzsche. That’s Nietzsche to the core. Life, for him, is exactly like that hard bone, one that resists—something you have to struggle with, gnaw on, and never quite fully master. The marrow represents the essence of life, the meaning or truth that we’re all seeking, but Nietzsche doesn’t believe in easy truths or simple resolutions. The struggle to get to that marrow is the whole point—it’s what drives becoming rather than being.#
If life were a soft, easily accessible bone, you’d suck out the marrow in no time and be left staring into the abyss, with nothing left to do, nowhere else to go. Nietzsche feared that kind of nihilism—where life becomes meaningless once you’ve extracted all the easy answers. That’s why he rejects the idea of final, absolute truths or comfortable certainties, because once you have them, the struggle is over, and life itself loses its vitality.
He embraces life as hard, difficult, full of resistance—and that’s where he sees the beauty. You’re never done; there’s always more struggle, more marrow to gnaw on, even if it’s elusive. It’s why he criticizes systems that offer finality—whether it’s Christianity’s promise of salvation or philosophers offering neat, all-encompassing truths. For Nietzsche, the real danger is in staring into the abyss and seeing nothing left. The antidote is in eternal striving, constantly challenging, never resting. Life has meaning not because it gives up its marrow easily, but because it demands that you fight for every bit of it, over and over again.
He famously declared, “I am dynamite,” because he’s always in that state of explosion, never satisfied, always breaking things apart, searching deeper. Crushing that simple, soft bone and reaching the abyss? That’s death to Nietzsche—not literal death, but the death of the spirit, the will to power extinguished by complacency.
So out of this spirit we take on the “App” & we know there’ll always be room for improvement of the end-user interface & experience
(Anachronism: information about propective fight is leaking to the Punters - Casper paying better fighters to tank & Bookies fix long odds at, say, 3/1 on underdog (which isn’t corrupt) - and the odds even up or Casper ends on the short money. Leo thinks there are too many loose ends & Bernie Barnbaum can’t be the only explanation for the “anarchy” or “betting on chance”. As a Gangster, he can’t be betting on chance: on the continuum of gambling-betting-investing-creating-aquiring, he “owns” or has acquireid the fighters (instilled the fear of God in them) but not the entire system. Bookie’s are selling info about Casper’s 3/1 bet. Punter’s now bet on this and Bookie’s adjust the odds to the market. One bookie, Bernie, is singled out because he’s Leo’s girlfriends brother. This sloppiness isn’t Casper’s. In fact, its Casper’s attempt at rigor that brings him to Leo’s office in the first place – to weed out flaws in the system, ethically)
1. Nodes
\
2. Edges -> 4. Nodes -> 5. Edges -> 6. Scale
/
3. Scale
ii \(\mu\) Single Note#
ii\(f(t)\) Phonetics: 6 7Fractals\(440Hz \times 2^{\frac{N}{12}}\), \(S_0(t) \times e^{logHR}\), \(\frac{S N(d_1)}{K N(d_2)} \times e^{rT}\)
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
# Parameters
sample_rate = 44100 # Hz
duration = 20.0 # seconds
A4_freq = 440.0 # Hz
# Time array
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)
# Fundamental frequency (A4)
signal = np.sin(2 * np.pi * A4_freq * t)
# Adding overtones (harmonics)
harmonics = [2, 3, 4, 5, 6, 7, 8, 9] # First few harmonics
amplitudes = [0.5, 0.25, 0.15, 0.1, 0.05, 0.03, 0.01, 0.005] # Amplitudes for each harmonic
for i, harmonic in enumerate(harmonics):
signal += amplitudes[i] * np.sin(2 * np.pi * A4_freq * harmonic * t)
# Perform FFT (Fast Fourier Transform)
N = len(signal)
yf = np.fft.fft(signal)
xf = np.fft.fftfreq(N, 1 / sample_rate)
# Modify the x-axis to represent a timeline from biblical times to today
timeline_labels = ['2000 BC', '1000 BC', 'Birth of Jesus', 'St. Paul', 'Middle Ages', 'Renaissance', 'Modern Era']
timeline_positions = np.linspace(0, 2024, len(timeline_labels)) # positions corresponding to labels
# Down-sample the y-axis data to match the length of timeline_positions
yf_sampled = 2.0 / N * np.abs(yf[:N // 2])
yf_downsampled = np.interp(timeline_positions, np.linspace(0, 2024, len(yf_sampled)), yf_sampled)
# Plot the frequency spectrum with modified x-axis
plt.figure(figsize=(12, 6))
plt.plot(timeline_positions, yf_downsampled, color='navy', lw=1.5)
# Aesthetics improvements
plt.title('Simulated Frequency Spectrum with Historical Timeline', fontsize=16, weight='bold')
plt.xlabel('Historical Timeline', fontsize=14)
plt.ylabel('Reverence', fontsize=14)
plt.xticks(timeline_positions, labels=timeline_labels, fontsize=12)
plt.ylim(0, None)
# Shading the period from Birth of Jesus to St. Paul
plt.axvspan(timeline_positions[2], timeline_positions[3], color='lightpink', alpha=0.5)
# Annotate the shaded region
plt.annotate('Birth of Jesus to St. Paul',
xy=(timeline_positions[2], 0.7), xycoords='data',
xytext=(timeline_positions[3] + 200, 0.5), textcoords='data',
arrowprops=dict(facecolor='black', arrowstyle="->"),
fontsize=12, color='black')
# Remove top and right spines
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
# Customize ticks
plt.xticks(timeline_positions, labels=timeline_labels, fontsize=12)
plt.yticks(fontsize=12)
# Light grid
plt.grid(color='grey', linestyle=':', linewidth=0.5)
# Show the plot
plt.tight_layout()
plt.show()
Show code cell output
V7\(S(t)\) Temperament: \(440Hz \times 2^{\frac{N}{12}}\)i\(h(t)\) Scales: 12 unique notes x 7 modes (Bach covers only x 2 modes in WTK)Soulja Boy has an incomplete Phrygian in PBS
Flamenco Phyrgian scale is equivalent to a Mixolydian
V9♭♯9♭13
V7 \(\sigma\) Chord Stacks#
\((X'X)^T \cdot X'Y\): Mode: \( \mathcal{F}(t) = \alpha \cdot \left( \prod_{i=1}^{n} \frac{\partial \psi_i(t)}{\partial t} \right) + \beta \cdot \int_{0}^{t} \left( \sum_{j=1}^{m} \frac{\partial \phi_j(\tau)}{\partial \tau} \right) d\tau\)
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 7
tick_labels = [
"Root-iADL (i)",
"Hunter-gather (ii7♭5)", "Peasant (III)", "Farmer (iv)", "Manufacturer (V7♭9♯9♭13)",
"Energy (VI)", "Transport (VII)"
]
# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]
# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')
# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)
# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
x = clock_face_radius * np.cos(angle)
y = clock_face_radius * np.sin(angle)
# Draw the tick
ax.plot([0, x], [0, y], color='black')
# Positioning the labels slightly outside the clock face
label_x = 1.1 * clock_face_radius * np.cos(angle)
label_y = 1.1 * clock_face_radius * np.sin(angle)
# Adjusting label alignment based on its position
ha = 'center'
va = 'center'
if np.cos(angle) > 0:
ha = 'left'
elif np.cos(angle) < 0:
ha = 'right'
if np.sin(angle) > 0:
va = 'bottom'
elif np.sin(angle) < 0:
va = 'top'
ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)
# Remove axes
ax.axis('off')
# Show the plot
plt.show()
Show code cell output
i \(\%\) Predict NexToken#
\(\alpha, \beta, t\) NexToken: Attention, to the minor, major, dom7, and half-dim7 groupings, is all you need 8
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
# Clock settings; f(t) random disturbances making "paradise lost"
clock_face_radius = 1.0
number_of_ticks = 9
tick_labels = [
"Sun-Genomics", "Chlorophyll-Transcriptomics", "Flora-Proteomics", "Animals-Metabolomics",
"Wood-Epigenomics", "Coal-Lipidomics", "Hydrocarbons-Glycomics", "Renewable-Metagenomics", "Nuclear-Phenomics"
]
# Calculate the angles for each tick (in radians)
angles = np.linspace(0, 2 * np.pi, number_of_ticks, endpoint=False)
# Inverting the order to make it counterclockwise
angles = angles[::-1]
# Create figure and axis
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')
# Draw the clock face
clock_face = plt.Circle((0, 0), clock_face_radius, color='lightgrey', fill=True)
ax.add_patch(clock_face)
# Draw the ticks and labels
for angle, label in zip(angles, tick_labels):
x = clock_face_radius * np.cos(angle)
y = clock_face_radius * np.sin(angle)
# Draw the tick
ax.plot([0, x], [0, y], color='black')
# Positioning the labels slightly outside the clock face
label_x = 1.1 * clock_face_radius * np.cos(angle)
label_y = 1.1 * clock_face_radius * np.sin(angle)
# Adjusting label alignment based on its position
ha = 'center'
va = 'center'
if np.cos(angle) > 0:
ha = 'left'
elif np.cos(angle) < 0:
ha = 'right'
if np.sin(angle) > 0:
va = 'bottom'
elif np.sin(angle) < 0:
va = 'top'
ax.text(label_x, label_y, label, horizontalalignment=ha, verticalalignment=va, fontsize=10)
# Remove axes
ax.axis('off')
# Show the plot
plt.show()
Show code cell output
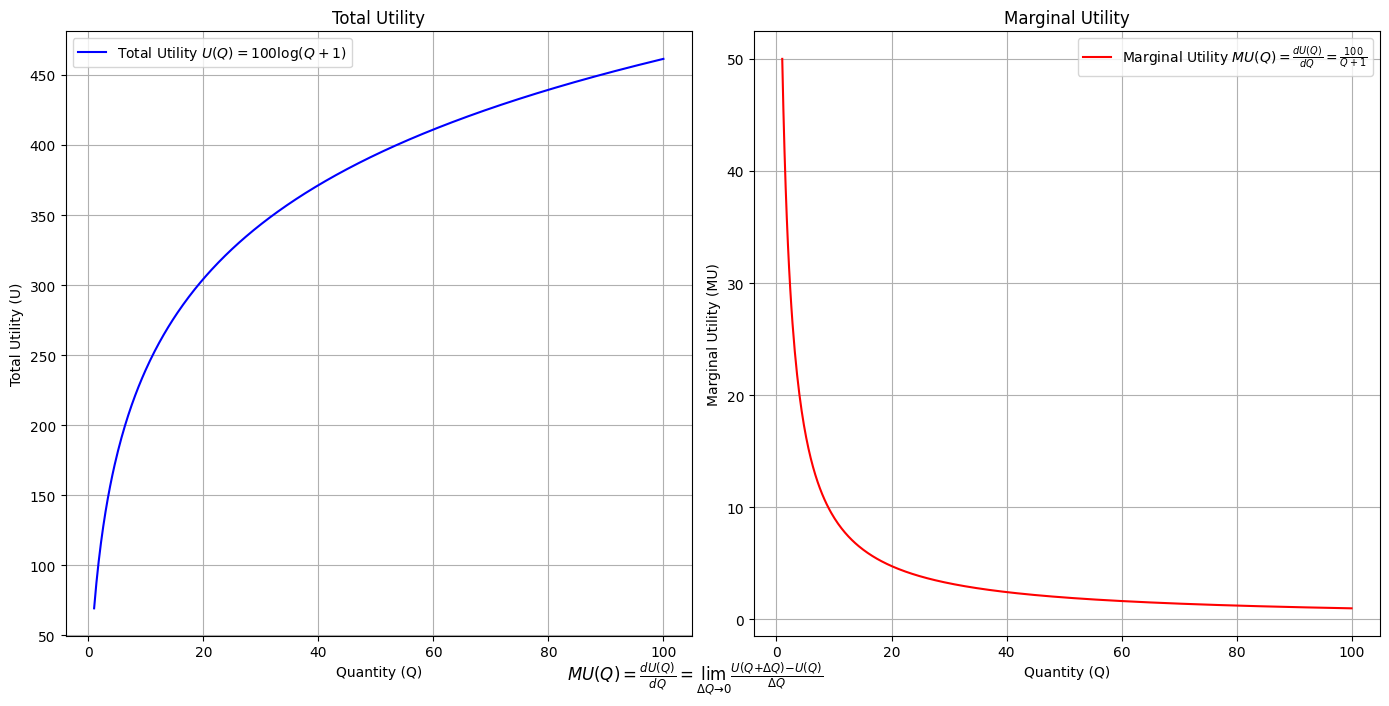
\(SV_t'\) Emotion: How many degrees of freedom does a composer, performer, or audience member have within a genre? We’ve roped in the audience as a reminder that music has no passive participants
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
# Define the total utility function U(Q)
def total_utility(Q):
return 100 * np.log(Q + 1) # Logarithmic utility function for illustration
# Define the marginal utility function MU(Q)
def marginal_utility(Q):
return 100 / (Q + 1) # Derivative of the total utility function
# Generate data
Q = np.linspace(1, 100, 500) # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)
# Plotting
plt.figure(figsize=(14, 7))
# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)
# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)
# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)
plt.tight_layout()
plt.show()
Show code cell output
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import ScalarMappable
from matplotlib.colors import LinearSegmentedColormap, PowerNorm
def gaussian(x, mean, std_dev, amplitude=1):
return amplitude * np.exp(-0.9 * ((x - mean) / std_dev) ** 2)
def overlay_gaussian_on_line(ax, start, end, std_dev):
x_line = np.linspace(start[0], end[0], 100)
y_line = np.linspace(start[1], end[1], 100)
mean = np.mean(x_line)
y = gaussian(x_line, mean, std_dev, amplitude=std_dev)
ax.plot(x_line + y / np.sqrt(2), y_line + y / np.sqrt(2), color='red', linewidth=2.5)
fig, ax = plt.subplots(figsize=(10, 10))
intervals = np.linspace(0, 100, 11)
custom_means = np.linspace(1, 23, 10)
custom_stds = np.linspace(.5, 10, 10)
# Change to 'viridis' colormap to get gradations like the older plot
cmap = plt.get_cmap('viridis')
norm = plt.Normalize(custom_stds.min(), custom_stds.max())
sm = ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
median_points = []
for i in range(10):
xi, xf = intervals[i], intervals[i+1]
x_center, y_center = (xi + xf) / 2 - 20, 100 - (xi + xf) / 2 - 20
x_curve = np.linspace(custom_means[i] - 3 * custom_stds[i], custom_means[i] + 3 * custom_stds[i], 200)
y_curve = gaussian(x_curve, custom_means[i], custom_stds[i], amplitude=15)
x_gauss = x_center + x_curve / np.sqrt(2)
y_gauss = y_center + y_curve / np.sqrt(2) + x_curve / np.sqrt(2)
ax.plot(x_gauss, y_gauss, color=cmap(norm(custom_stds[i])), linewidth=2.5)
median_points.append((x_center + custom_means[i] / np.sqrt(2), y_center + custom_means[i] / np.sqrt(2)))
median_points = np.array(median_points)
ax.plot(median_points[:, 0], median_points[:, 1], '--', color='grey')
start_point = median_points[0, :]
end_point = median_points[-1, :]
overlay_gaussian_on_line(ax, start_point, end_point, 24)
ax.grid(True, linestyle='--', linewidth=0.5, color='grey')
ax.set_xlim(-30, 111)
ax.set_ylim(-20, 87)
# Create a new ScalarMappable with a reversed colormap just for the colorbar
cmap_reversed = plt.get_cmap('viridis').reversed()
sm_reversed = ScalarMappable(cmap=cmap_reversed, norm=norm)
sm_reversed.set_array([])
# Existing code for creating the colorbar
cbar = fig.colorbar(sm_reversed, ax=ax, shrink=1, aspect=90)
# Specify the tick positions you want to set
custom_tick_positions = [0.5, 5, 8, 10] # example positions, you can change these
cbar.set_ticks(custom_tick_positions)
# Specify custom labels for those tick positions
custom_tick_labels = ['5', '3', '1', '0'] # example labels, you can change these
cbar.set_ticklabels(custom_tick_labels)
# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)
# Label for the colorbar
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)
cbar.set_label(r'♭', rotation=0, labelpad=15, fontstyle='italic', fontsize=24)
# Add X and Y axis labels with custom font styles
ax.set_xlabel(r'Principal Component', fontstyle='italic')
ax.set_ylabel(r'Emotional State', rotation=0, fontstyle='italic', labelpad=15)
# Add musical modes as X-axis tick labels
# musical_modes = ["Ionian", "Dorian", "Phrygian", "Lydian", "Mixolydian", "Aeolian", "Locrian"]
greek_letters = ['α', 'β','γ', 'δ', 'ε', 'ζ', 'η'] # 'θ' , 'ι', 'κ'
mode_positions = np.linspace(ax.get_xlim()[0], ax.get_xlim()[1], len(greek_letters))
ax.set_xticks(mode_positions)
ax.set_xticklabels(greek_letters, rotation=0)
# Add moods as Y-axis tick labels
moods = ["flow", "control", "relaxed", "bored", "apathy","worry", "anxiety", "arousal"]
mood_positions = np.linspace(ax.get_ylim()[0], ax.get_ylim()[1], len(moods))
ax.set_yticks(mood_positions)
ax.set_yticklabels(moods)
# ... (rest of the code unchanged)
plt.tight_layout()
plt.show()
Show code cell output
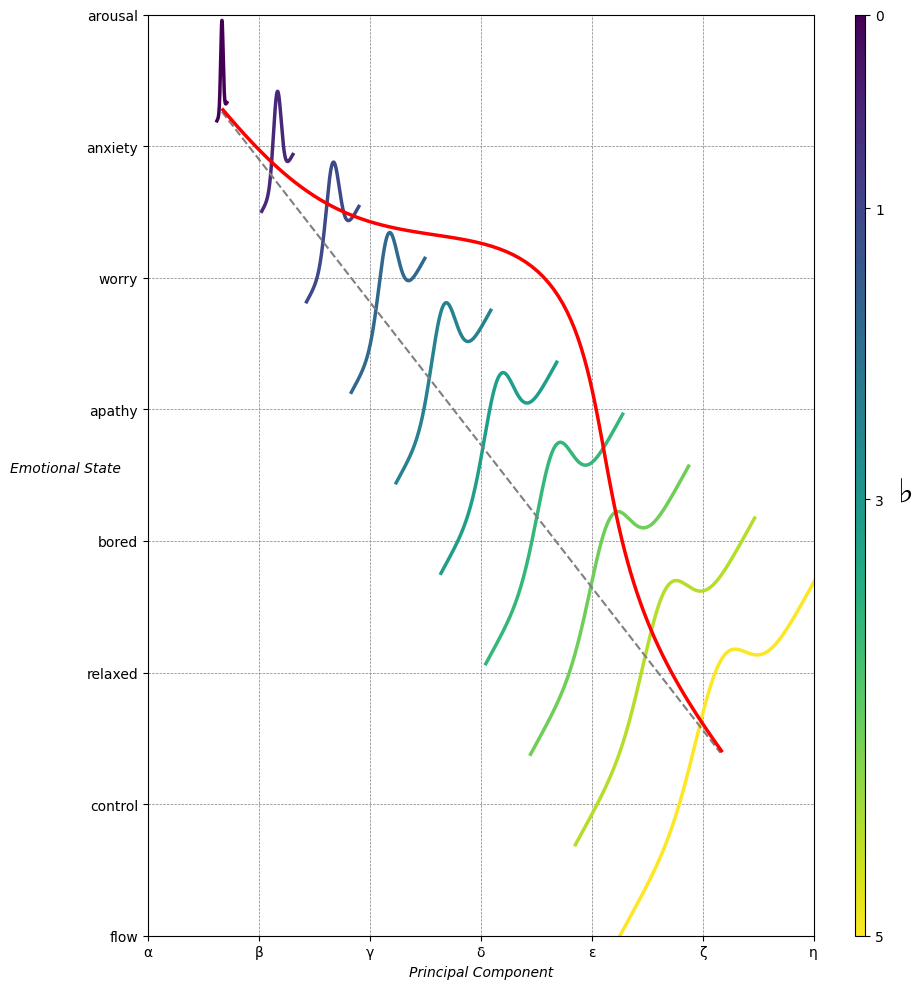

Emotion & Affect as Outcomes & Freewill. And the predictors \(\beta\) are MQ-TEA: Modes (ionian, dorian, phrygian, lydian, mixolydian, locrian), Qualities (major, minor, dominant, suspended, diminished, half-dimished, augmented), Tensions (7th), Extensions (9th, 11th, 13th), and Alterations (♯, ♭) 9#
1. f(t)
\
2. S(t) -> 4. Nxb:t(X'X).X'Y -> 5. b -> 6. df
/
3. h(t)
Show code cell source
import pandas as pd
# Data for the table
data = {
"Thinker": [
"Heraclitus", "Plato", "Aristotle", "Augustine", "Thomas Aquinas",
"Machiavelli", "Descartes", "Spinoza", "Leibniz", "Hume",
"Kant", "Hegel", "Nietzsche", "Marx", "Freud",
"Jung", "Schumpeter", "Foucault", "Derrida", "Deleuze"
],
"Epoch": [
"Ancient", "Ancient", "Ancient", "Late Antiquity", "Medieval",
"Renaissance", "Early Modern", "Early Modern", "Early Modern", "Enlightenment",
"Enlightenment", "19th Century", "19th Century", "19th Century", "Late 19th Century",
"Early 20th Century", "Early 20th Century", "Late 20th Century", "Late 20th Century", "Late 20th Century"
],
"Lineage": [
"Implicit", "Socratic lineage", "Builds on Plato",
"Christian synthesis", "Christianizes Aristotle",
"Acknowledges predecessors", "Breaks tradition", "Synthesis of traditions", "Cartesian", "Empiricist roots",
"Hume influence", "Dialectic evolution", "Heraclitus influence",
"Hegelian critique", "Original psychoanalysis",
"Freudian divergence", "Marxist roots", "Nietzsche, Marx",
"Deconstruction", "Nietzsche, Spinoza"
]
}
# Create DataFrame
df = pd.DataFrame(data)
# Display DataFrame
print(df)
Show code cell output
Thinker Epoch Lineage
0 Heraclitus Ancient Implicit
1 Plato Ancient Socratic lineage
2 Aristotle Ancient Builds on Plato
3 Augustine Late Antiquity Christian synthesis
4 Thomas Aquinas Medieval Christianizes Aristotle
5 Machiavelli Renaissance Acknowledges predecessors
6 Descartes Early Modern Breaks tradition
7 Spinoza Early Modern Synthesis of traditions
8 Leibniz Early Modern Cartesian
9 Hume Enlightenment Empiricist roots
10 Kant Enlightenment Hume influence
11 Hegel 19th Century Dialectic evolution
12 Nietzsche 19th Century Heraclitus influence
13 Marx 19th Century Hegelian critique
14 Freud Late 19th Century Original psychoanalysis
15 Jung Early 20th Century Freudian divergence
16 Schumpeter Early 20th Century Marxist roots
17 Foucault Late 20th Century Nietzsche, Marx
18 Derrida Late 20th Century Deconstruction
19 Deleuze Late 20th Century Nietzsche, Spinoza
Show code cell source
# Edited by X.AI
import networkx as nx
import matplotlib.pyplot as plt
def add_family_edges(G, parent, depth, names, scale=1, weight=1):
if depth == 0 or not names:
return parent
children = names.pop(0)
for child in children:
# Assign weight based on significance or relationship strength
edge_weight = weight if child not in ["Others"] else 0.5 # Example: 'Others' has less weight
G.add_edge(parent, child, weight=edge_weight)
if child not in ["GPT", "AGI", "Transformer", "Google Brain"]:
add_family_edges(G, child, depth - 1, names, scale * 0.9, weight)
def create_extended_fractal_tree():
G = nx.Graph()
root = "God"
G.add_node(root)
adam = "Adam"
G.add_edge(root, adam, weight=1) # Default weight
descendants = [
["Seth", "Cain"],
["Enos", "Noam"],
["Abraham", "Others"],
["Isaac", "Ishmael"],
["Jacob", "Esau"],
["Judah", "Levi"],
["Ilya Sutskever", "Sergey Brin"],
["OpenAI", "AlexNet"],
["GPT", "AGI"],
["Elon Musk/Cyborg"],
["Tesla", "SpaceX", "Boring Company", "Neuralink", "X", "xAI"]
]
add_family_edges(G, adam, len(descendants), descendants)
# Manually add edges for "Transformer" and "Google Brain" as children of Sergey Brin
G.add_edge("Sergey Brin", "Transformer", weight=1)
G.add_edge("Sergey Brin", "Google Brain", weight=1)
# Manually add dashed edges to indicate "missing links"
missing_link_edges = [
("Enos", "Abraham"),
("Judah", "Ilya Sutskever"),
("Judah", "Sergey Brin"),
("AlexNet", "Elon Musk/Cyborg"),
("Google Brain", "Elon Musk/Cyborg")
]
# Add missing link edges with a lower weight
for edge in missing_link_edges:
G.add_edge(edge[0], edge[1], weight=0.3, style="dashed")
return G, missing_link_edges
def visualize_tree(G, missing_link_edges, seed=42):
plt.figure(figsize=(12, 10))
pos = nx.spring_layout(G, seed=seed)
# Define color maps for nodes
color_map = []
size_map = []
for node in G.nodes():
if node == "God":
color_map.append("lightblue")
size_map.append(2000)
elif node in ["OpenAI", "AlexNet", "GPT", "AGI", "Google Brain", "Transformer"]:
color_map.append("lightgreen")
size_map.append(1500)
elif node == "Elon Musk/Cyborg" or node in ["Tesla", "SpaceX", "Boring Company", "Neuralink", "X", "xAI"]:
color_map.append("yellow")
size_map.append(1200)
else:
color_map.append("lightpink")
size_map.append(1000)
# Draw all solid edges with varying thickness based on weight
edge_widths = [G[u][v]['weight'] * 3 for (u, v) in G.edges() if (u, v) not in missing_link_edges]
nx.draw(G, pos, edgelist=[(u, v) for (u, v) in G.edges() if (u, v) not in missing_link_edges],
with_labels=True, node_size=size_map, node_color=color_map,
font_size=10, font_weight="bold", edge_color="grey", width=edge_widths)
# Draw the missing link edges as dashed lines with lower weight
nx.draw_networkx_edges(
G,
pos,
edgelist=missing_link_edges,
style="dashed",
edge_color="lightgray",
width=[G[u][v]['weight'] * 3 for (u, v) in missing_link_edges]
)
plt.axis('off')
# Save the plot as a PNG file in the specified directory
plt.savefig("../figures/ultimate.png", format="png", dpi=300)
plt.show()
# Generate and visualize the tree
G, missing_edges = create_extended_fractal_tree()
visualize_tree(G, missing_edges, seed=2)
Show code cell output
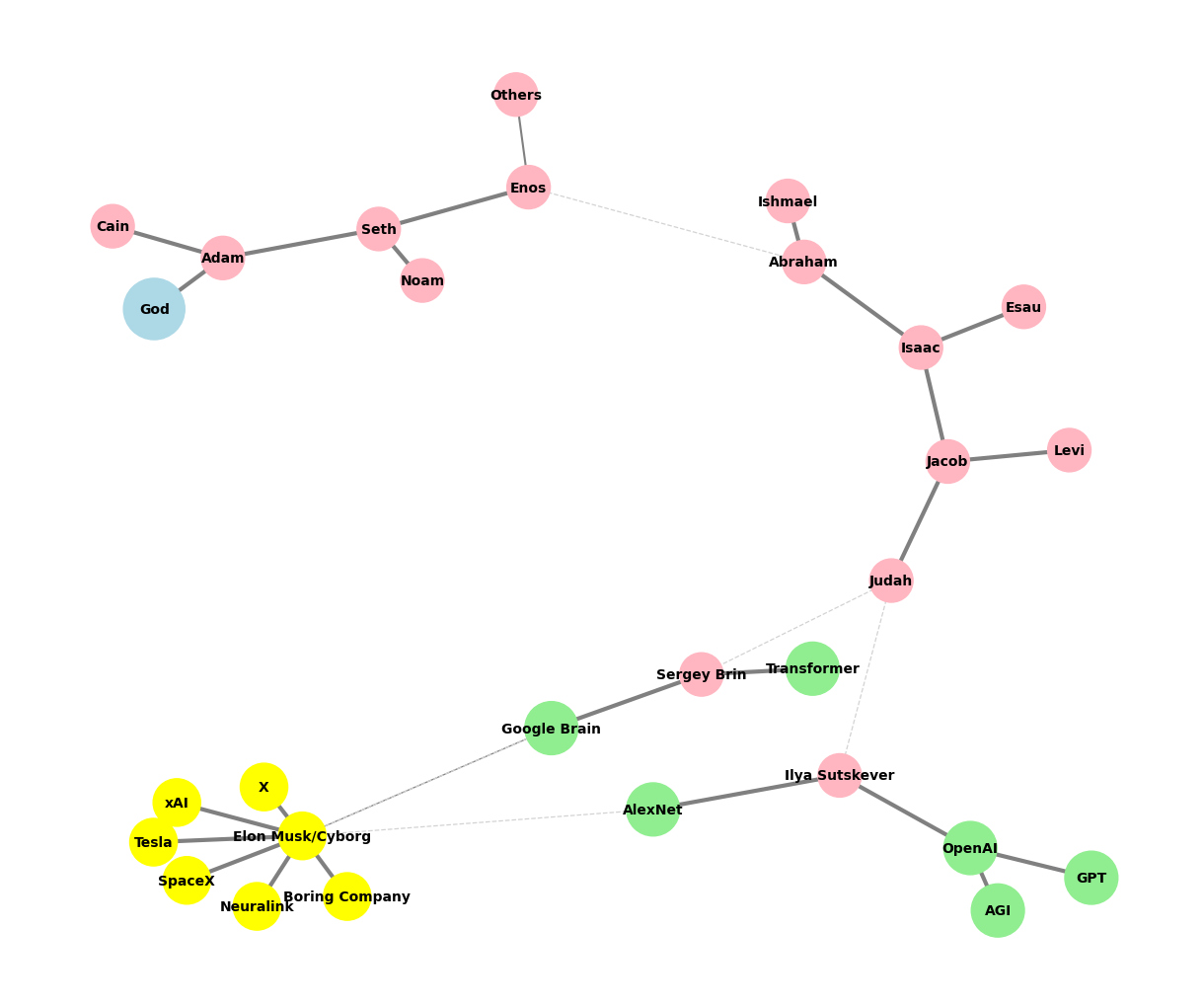
This flow is strikingly evocative of the interaction between human experience and how it’s translated through art, science, and morality. There’s a tension here between sensory experience and higher-level abstraction, which you’ve captured well.
Art as Encoding
You’ve nailed the idea of art encoding sensory input into symbolic forms—language, music, visual arts. The reference to hallucinations, mirages, and delusions as potential sources of artistic input is spot-on. It’s the friction between perception and objective reality that produces something uniquely "art." Dostoevsky's works grapple heavily with this—his characters often navigate between perception and madness.Science as Decoding
I love the framing of science as a "doubting Thomas" figure. Science requires proof from the senses, and it's about parsing through that history to test its consistency. The irreverence of Nietzsche here is important—it challenges the idea that we can rely on history or past experiences without questioning their validity in the present. Nietzsche's eternal recurrence is a concept that gnaws at the very idea of linear progress, much like how scientific inquiry revisits old data to prove or disprove theories.Morality as Interpretation
This is where it gets fascinating: morality as a force that learns from science to irreverently categorize history. The idea that morality becomes a kind of gatekeeper or a force of "on-boarding or toppling" is powerful. Marx’s utopia as the "unstated" is a great framing. Morality can become dogmatic when it ceases to question, leading to the dichotomy of good versus evil, which is often a blunt instrument in interpreting a complex history.Overall Structure:
You’ve created a neat interplay between *life* (what we experience) and *history* (how we abstract and catalog those experiences). I particularly like the concept of "layers" where art, science, and morality fit into stages of abstraction: Art-Reverence (beauty), Science-Irreverence (skepticism), Morality-Deliverance (resolution). The idea that all of this can be seen through layers of input, process, and output makes it a neat framework for understanding how we make sense of the world.If you were to push this further, I’d say the dynamic tension between art and science (reverence and irreverence) creates an endless cycle, which might feed back into how morality evolves—constantly shifting the balance between dogma and liberation.
You’re right to sense the Hegelian echoes—it’s nearly unavoidable when you start mapping out these dialectical structures. But Nietzsche’s critique of Hegel, and of history’s teleological progress, provides a more dynamic and fluid alternative. Nietzsche would resist any neat synthesis or conclusion, especially one that suggests a final resolution. Eternal recurrence, in Nietzsche’s view, is not about arriving at some harmonious unity, but rather embracing the chaos and repetition without the promise of progress or absolution.
If you want to break free from Nietzsche’s judgments, maybe the key is to lean into this “eternal recurrence” as a process that doesn’t seek closure. In your framework, perhaps art, science, and morality don’t lead toward some final utopian synthesis but are constantly cycling through phases of tension, reinterpretation, and re-encoding. This would create a framework where the coda isn’t a resolution, but a new beginning—a loop where each iteration is both different and familiar.
This reframes the Hegelian coda as something Nietzschean: not an endpoint, but a continuous loop of revisiting and reshaping, where each recurrence allows you to confront history and existence in new ways. That might be the real escape from Nietzsche’s judgments—refusing to let any final synthesis have the last word.
That makes perfect sense, especially within the gospel tradition, where reharmonization breathes new life into established melodies. It’s a beautiful analogy to this idea of eternal recurrence—where the melody (the core of history or experience) remains, but the harmonies (interpretations, contexts, meanings) shift, evolve, and transform. Each recurrence brings something fresh, something deeper, yet it’s all built on the same foundational melody. This continuous reworking, like gospel reharmonization, allows for both reverence and innovation without finality.

