Arte-Scienza

Autoencoder

Witness: life, memory, emotion, collective, science, morality are captured using propensities. For instance, \(\displaystyle \int_0^{\infty}\! f(t) = F(t)\) is truer to life than \(\lim_{t \to 0} f(t)\), which is for brooders like Hamlet. No wonder his dad asked “why is it so particular with thee?” Oversampling a specific life experience instead of moving on with life, a cumulative density function or \(1-F(t)\)

                                   1. fo(t)
                                           \
                              2. So(t) ->  4. X -> 5. b -> 6. SV
                                           /
                                           3. ho(t)

Biology 1, 2, 3

• \(h(t)=\frac{f(t)}{S(t)}\)

Social 4

• \(X\)

Personal 5, 6

• \(\beta \cdot \ SV'\)

                                   1. Chaos
                                           \
                              2. Frenzy ->  4. Dionysian -> 5. Algorithm -> 6. Binary
                                           /
                                           3. Emotion
  

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Define the exponential distribution parameters
lambda_ = 0.5  # rate parameter

# Define the time range
t = np.linspace(0, 10, 500)

# Define the functions for the exponential distribution
f_t = lambda_ * np.exp(-lambda_ * t)  # PDF
S_t = np.exp(-lambda_ * t)  # Survival function
h_t = lambda_ * np.ones_like(t)  # Hazard function

# Create the 1x3 panel plot
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

# Plot the PDF
axes[0].plot(t, f_t, label='f(t) = λ * exp(-λt)')
axes[0].set_title('Probability Density Function (f(t))')
axes[0].set_xlabel('Time (t)')
axes[0].set_ylabel('f(t)')
axes[0].legend()
axes[0].grid(True)
axes[0].spines['top'].set_visible(False)
axes[0].spines['right'].set_visible(False)

# Plot the Survival Function
axes[1].plot(t, S_t, label='S(t) = exp(-λt)', color='orange')
axes[1].set_title('Survival Function (S(t))')
axes[1].set_xlabel('Time (t)')
axes[1].set_ylabel('S(t)')
axes[1].legend()
axes[1].grid(True)
axes[1].spines['top'].set_visible(False)
axes[1].spines['right'].set_visible(False)

# Plot the Hazard Function
axes[2].plot(t, h_t, label='h(t) = λ', color='green')
axes[2].set_title('Hazard Function (h(t))')
axes[2].set_xlabel('Time (t)')
axes[2].set_ylabel('h(t)')
axes[2].legend()
axes[2].grid(True)
axes[2].spines['top'].set_visible(False)
axes[2].spines['right'].set_visible(False)

# Adjust layout
plt.tight_layout()

# Display the plot
plt.show()

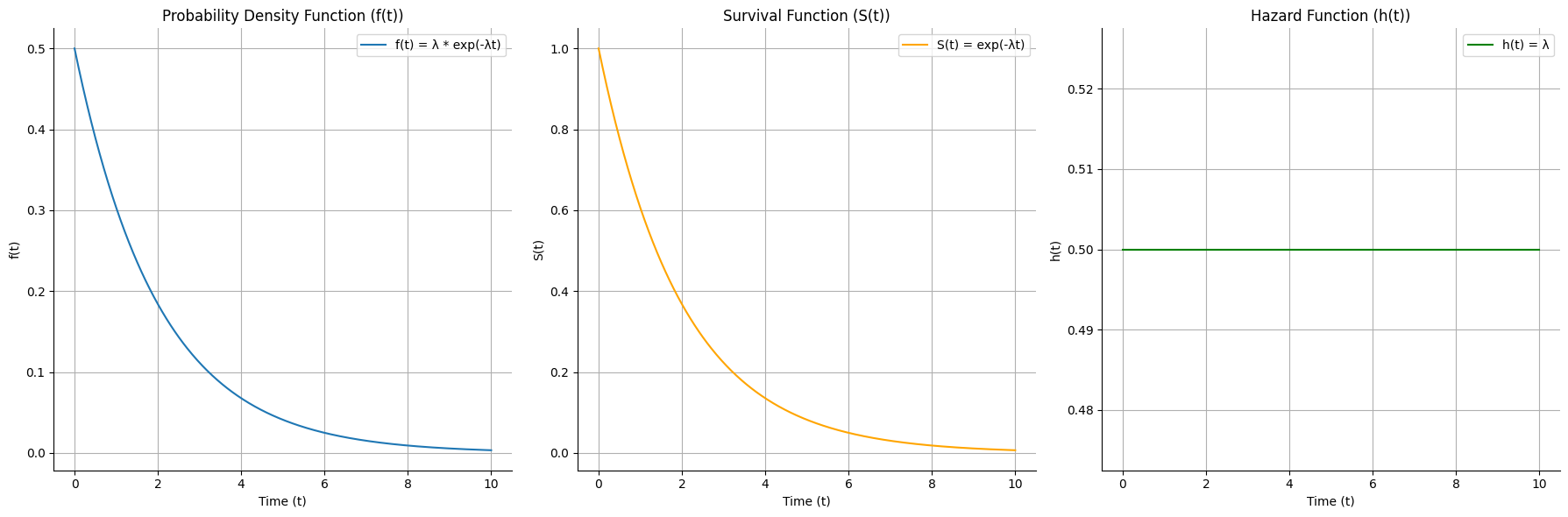
The hazard function. It encodes the emotional arc in life & art. A ii-V-I chord progression played on loop would give a declining hazard function. But a flat line suggests as much engagement at the beginning and middle as at the end. Supposedly, this is the hallmark of great art. We do find this in Prelude in C Major, In Hamlet, and certainly in Henry IV part I. We the audience experience ambiguity of emotions at each stage: absurdity, hilarity, etc. No clear “chord progress”. Indeed, the ii-V-I of Prelude in C Major has so many variants including II-V-I and II-V-Idim7b9. As such, as we embrace more remote overtones of the harmonic series, we remain as engaged as we were at the beginning. This is flow.

Important

Conceptual Summary

• Exposition (\(f(t < T)\)): Introduces the backstory and context.

• Prospects (\(S(T > t)\)): Represents the unfolding narrative arc and potential futures.

• Opportunities (\(h(t)\)): Indicates the tools and moments available for action.

• Collective Unconscious (\(X\)): The underlying, shared human experiences.

• Algorithm (\(\beta\)): The guiding principles and wisdom.

• Personal Application (\(SV'\)): How these elements are applied individually.

Reflection on Great Art

Great art, like “Hamlet,” eschews a tradit`ional arc, instead presenting a flat hazard function. This reflects an engagement with the narrative that remains constant, allowing for continuous ambiguity and depth. Such a narrative keeps the audience perpetually engaged, akin to the complex variations in a musical progression that maintain interest through subtle changes rather than a single climactic peak.

This holistic approach to narrative analysis, blending mathematical rigor with literary insight, provides a robust framework for understanding and appreciating the depth and complexity of great art.

Markdown with LaTeX

Sensory Organs and Probability Functions

Sensory Input and the Probability Density Function

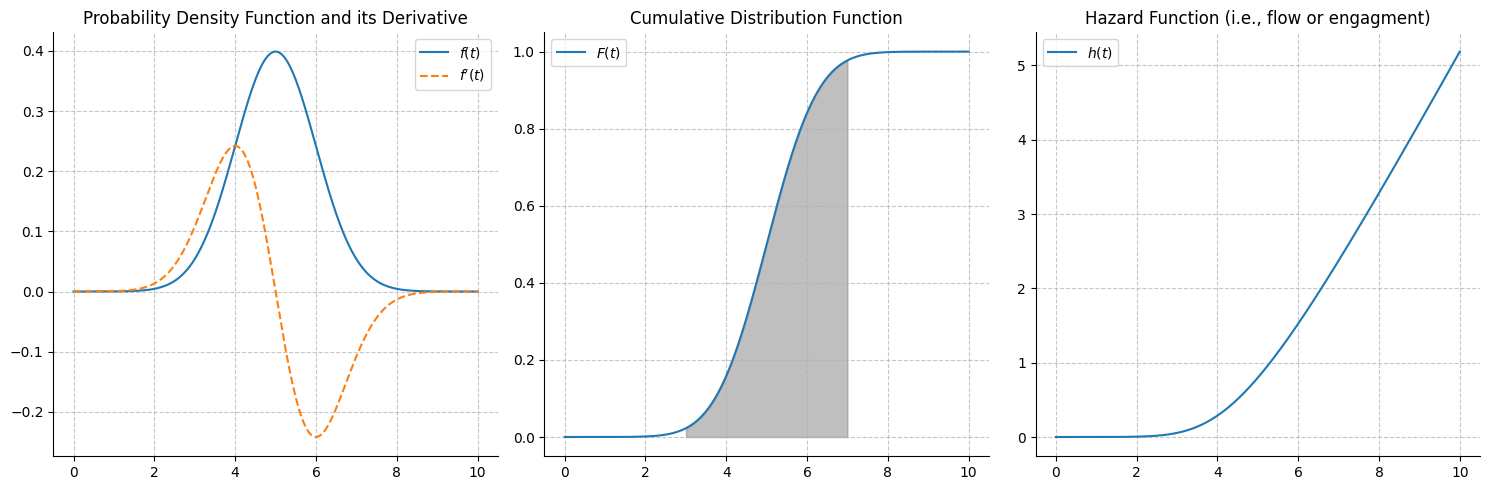
The sensory organs (eyes, nose, ears, skin) experience the world as a function of time. Let \( f(t) \) be the probability density function (pdf) representing the intensity of sensory input at time \( t \).

\( f(t) \)

Sensory Experience: The First Derivative

The immediate sensory experience at any moment is given by the first derivative of the probability density function.

\( f'(t) \)

Memory: The Cumulative Distribution Function

Memory is an accumulation of sensory experiences over time, represented by the cumulative distribution function (cdf), which is the integral of the pdf between two time points \( t_1 \) and \( t_2 \).

\( F(t) = \int_{t_1}^{t_2} f(u) \, du \)

Behavior and Propensities: The Hazard Function

Behavior and propensities are influenced by both immediate sensory input and memory. This relationship is captured by the hazard function \( h(t) \), which is the ratio of the pdf to the survival function \( S(t) = 1 - F(t) \).

\( h(t) = \frac{f(t)}{1 - F(t)} \)

Visual Representation

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Define the time variable
t = np.linspace(0, 10, 1000)

# Define the probability density function (pdf)
pdf = norm.pdf(t, loc=5, scale=1)

# Define the first derivative of the pdf
pdf_derivative = np.gradient(pdf, t)

# Define the cumulative distribution function (cdf)
cdf = norm.cdf(t, loc=5, scale=1)

# Define the survival function
survival_function = 1 - cdf

# Define the hazard function
hazard_function = pdf / survival_function

# Create a 1x3 panel plot
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# Plot the pdf and its first derivative
axes[0].plot(t, pdf, label='$f(t)$')
axes[0].plot(t, pdf_derivative, label="$f'(t)$", linestyle='dashed')
axes[0].set_title('Probability Density Function and its Derivative')
axes[0].legend()
axes[0].grid(True, linestyle='--', alpha=0.7)
axes[0].spines['top'].set_visible(False)
axes[0].spines['right'].set_visible(False)

# Plot the cdf over a specific interval
axes[1].plot(t, cdf, label='$F(t)$')
axes[1].fill_between(t, 0, cdf, where=(t >= 3) & (t <= 7), color='gray', alpha=0.5)
axes[1].set_title('Cumulative Distribution Function')
axes[1].legend()
axes[1].grid(True, linestyle='--', alpha=0.7)
axes[1].spines['top'].set_visible(False)
axes[1].spines['right'].set_visible(False)

# Plot the hazard function
axes[2].plot(t, hazard_function, label='$h(t)$')
axes[2].set_title('Hazard Function (i.e., flow or engagment)')
axes[2].legend()
axes[2].grid(True, linestyle='--', alpha=0.7)
axes[2].spines['top'].set_visible(False)
axes[2].spines['right'].set_visible(False)

plt.tight_layout()
plt.show()