Apollo & Dionysus#
History is a fractal unfolding of entropy and order, a ceaseless churn wherein civilizations rise on the back of extracted resources, only to collapse under the weight of their own complexity
History. It’s a fractal unfolding of entropy and order, a ceaseless churn wherein civilizations rise on the back of extracted resources, only to collapse under the weight of their own complexity
— Yours Truly
Show code cell source
import matplotlib.pyplot as plt
import numpy as np
def draw_branch(x, y, angle, depth, length, ax):
if depth == 0:
return
x_end = x + length * np.cos(angle)
y_end = y + length * np.sin(angle)
ax.plot([x, x_end], [y, y_end], 'k-', lw=2)
new_length = length * 0.7
draw_branch(x_end, y_end, angle - np.pi/6, depth - 1, new_length, ax)
draw_branch(x_end, y_end, angle + np.pi/6, depth - 1, new_length, ax)
fig, ax = plt.subplots(figsize=(6, 8))
ax.set_xticks([])
ax.set_yticks([])
ax.set_frame_on(False)
draw_branch(0, -1, np.pi/2, 10, 1, ax)
plt.show()
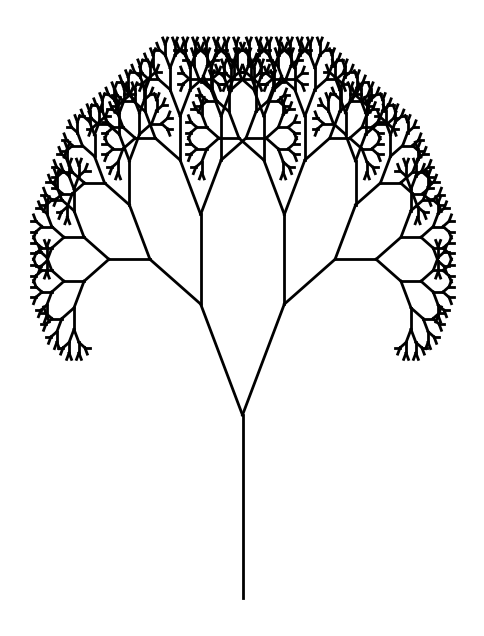

Fig. 13 Strange Attractor (Chaotic System). This code simulates a simple chaotic attractor using the Lorenz system.#
Show code cell source
from scipy.integrate import solve_ivp
import numpy as np
import matplotlib.pyplot as plt
def lorenz(t, state, sigma=10, beta=8/3, rho=28):
x, y, z = state
dxdt = sigma * (y - x)
dydt = x * (rho - z) - y
dzdt = x * y - beta * z
return [dxdt, dydt, dzdt]
t_span = (0, 50)
initial_state = [0.1, 0.0, 0.0]
t_eval = np.linspace(t_span[0], t_span[1], 10000)
sol = solve_ivp(lorenz, t_span, initial_state, t_eval=t_eval)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
ax.plot(sol.y[0], sol.y[1], sol.y[2], lw=0.5)
ax.set_title("Lorenz Attractor (Chaotic System)")
plt.show()
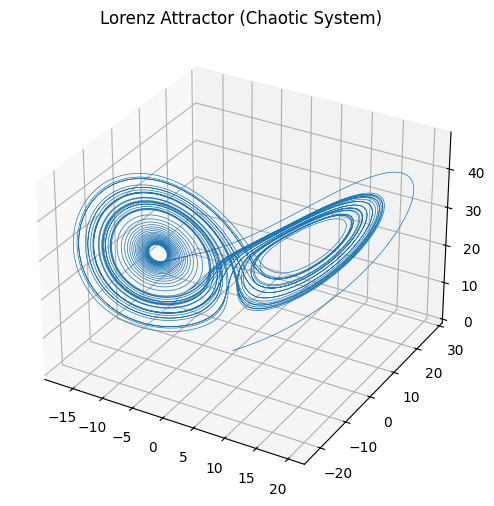

Fig. 14 Fractal Structure (Self-Similarity). A visualization of the famous Mandelbrot fractal, representing infinite complexity at all scales.#
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
def mandelbrot(c, max_iter=100):
z = c
for n in range(max_iter):
if abs(z) > 2:
return n
z = z*z + c
return max_iter
xmin, xmax, ymin, ymax = -2.0, 1.0, -1.5, 1.5
width, height = 1000, 1000
x = np.linspace(xmin, xmax, width)
y = np.linspace(ymin, ymax, height)
mandelbrot_set = np.zeros((width, height))
for i in range(width):
for j in range(height):
mandelbrot_set[i, j] = mandelbrot(complex(x[i], y[j]))
plt.figure(figsize=(8, 8))
plt.imshow(mandelbrot_set.T, extent=[xmin, xmax, ymin, ymax], cmap="inferno")
plt.title("Mandelbrot Set (Fractal Structure)")
plt.colorbar()
plt.show()
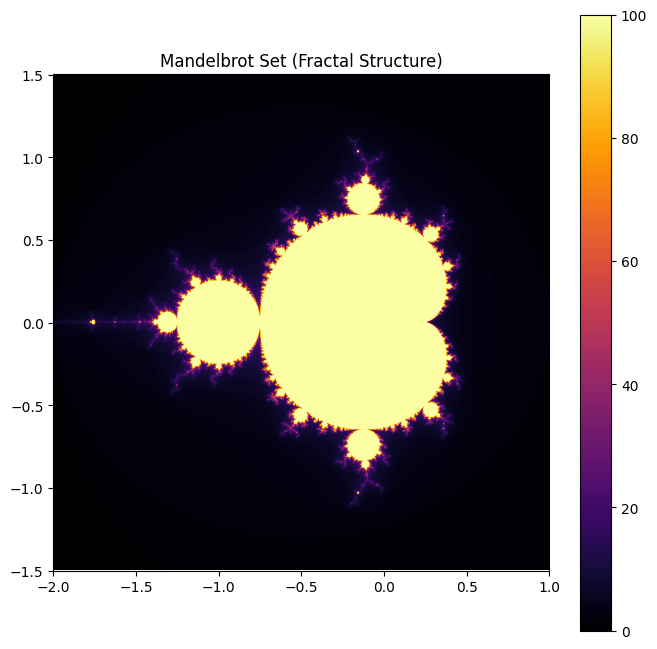

Fig. 15 Immitation. This is what distinguishes humans (really? self-similar is all fractal). We reproduce language, culture, music, behaviors, weapons of extraordinarily complex nature. A ritualization of these processes stablizes its elements and creates stability and uniformity, as well as opportunities for conflict and negotiation. These codes illustrate the key points made in Sapolsky’s discussion: the limits of reductionism, the role of chaos in biological systems, and the fundamental nature of self-similarity in complex structures.#

