Unknown

Unknown#

From the point of view of form, the type of all the arts is the art of the musician - Oscar Wilde

Missingness of one or all of the principle components of data, code, server, models, weights, and profiles is what is at stake (but perhaps migration represents redefining home?):

  • \(f(t)\) I

  • \(S(t)\) ii-V-I

  • \(h(t)\) iii, IV, vi, vii, alterations

    • Δ7

    • m or min

    • ° or dim

    • ø or m7♭5, -5

    • + or aug, ♯5 or +5

    • sus

    • ♭9, ♯9, ♯11, ♭13

  • \((X'X)^T \cdot X'Y\) tension & release (e.g. Aiim7/E (GΔ) - iim7♭5/E Em)

  • \(\beta\) m7♭5 > 7♯9 > 7♭9 > °7 > 7, etc

  • \(SV'\) BWV 846 Prelude in C Major, Op 28 Prelude No. 4

While Tyler Perry’s work captures the collective unconscious via tension (bad marriage) & release (church music), the characters he creates don’t have individually compelling arcs that subsume many of the parameters of life

This is equivalent to their \(SV'\) being a vector of mostly \(zeros\) and the barriers, challenges, diversions, sirens, misfortunes, obstacles, courses, “chains” within which Tyler Perry is supposed to “dance” aren’t rich, leaving a basic ii-V-I redemption arch with perhaps one or two straightforward insersions of, say, iii and IV.

      1. f(t)
            \
 2. S(t) -> 4. y:h'(t)=0;t(X'X)X'Y -> 5. b -> 6. SV'
            /
            3. h(t)

ii: Departure 1, 2, 3#

  • Sensory acuity: vision, hearing, smell, balance, glucose

  • Memory & cognitive: integrity, decline, tests

  • Physical activty: sarcopenia, brisk, dynamometer

V: Struggle 4#

  • Frailty: loneliness, isolation, usefulness

I: Return 5, 6#

  • Independence: ADLs, IADL

  • Hard-outcomes: shuffling, reflexes, falls, hospitalization, organ-failure, death

                         1. Pessimism
                                     \
            2. Beyond Good & Evil -> 4. Dionysian -> 5. Science -> 6. Morality
                                     /
                                     3. Robustness


                             1. Chaos
                                     \
                        2. Frenzy -> 4. Dionysian -> 5. Algorithm -> 6. Binary
                                     /
                                     3. Energy

Activation Function, \(Q\): 1st, 3rd, 5th, ♭♭7th, 9th#

  • Hunter-gatherer/War: humanism, spiritual teachings (I)

  • Peasant/Economics: judeo (B)

Biases, \(U()\): 11th, 13th#

  • Farmer/Calculus: christian (G)

  • Manufacturer/Philosophy: world religions (Y)

Weights, \(\frac{dU()}{dQ}\): ♯9,♭9,♯11,♭13#

  • Electricity/Musick: prophetic utterances (O)

  • Railway/Leisure: individual experience (R)

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

# Define the total utility function U(Q)
def total_utility(Q):
    return 100 * np.log(Q + 1)  # Logarithmic utility function for illustration

# Define the marginal utility function MU(Q)
def marginal_utility(Q):
    return 100 / (Q + 1)  # Derivative of the total utility function

# Generate data
Q = np.linspace(1, 100, 500)  # Quantity range from 1 to 100
U = total_utility(Q)
MU = marginal_utility(Q)

# Plotting
plt.figure(figsize=(14, 7))

# Plot Total Utility
plt.subplot(1, 2, 1)
plt.plot(Q, U, label=r'Total Utility $U(Q) = 100 \log(Q + 1)$', color='blue')
plt.title('Total Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Total Utility (U)')
plt.legend()
plt.grid(True)

# Plot Marginal Utility
plt.subplot(1, 2, 2)
plt.plot(Q, MU, label=r'Marginal Utility $MU(Q) = \frac{dU(Q)}{dQ} = \frac{100}{Q + 1}$', color='red')
plt.title('Marginal Utility')
plt.xlabel('Quantity (Q)')
plt.ylabel('Marginal Utility (MU)')
plt.legend()
plt.grid(True)

# Adding some calculus notation and Greek symbols
plt.figtext(0.5, 0.02, r"$MU(Q) = \frac{dU(Q)}{dQ} = \lim_{\Delta Q \to 0} \frac{U(Q + \Delta Q) - U(Q)}{\Delta Q}$", ha="center", fontsize=12)

plt.tight_layout()
plt.show()
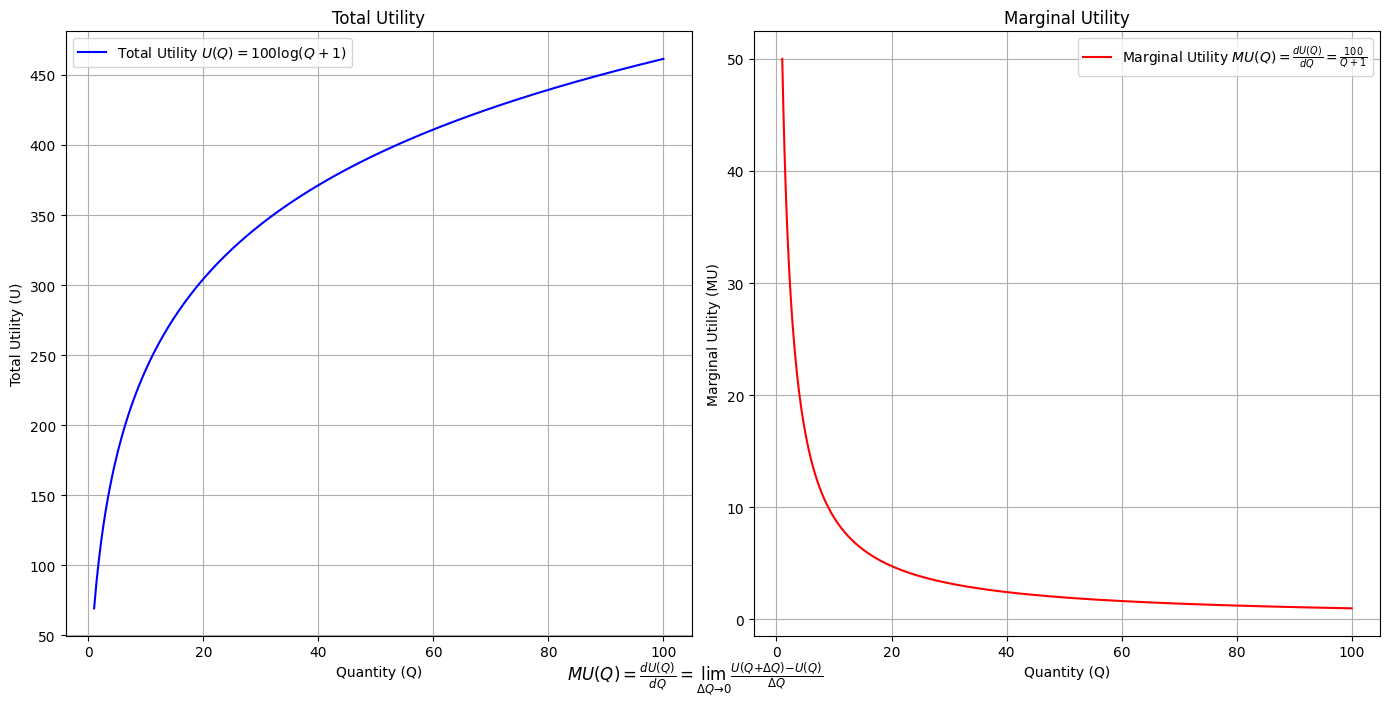
../_images/afa91f0bcf337e9d0a0901707fe1aa1c7a332b551fb5b7af920037b2996fc9ee.png

Running this code will generate a visual demonstration of diminishing marginal utility with appropriate calculus notation and Greek symbols.

Here is the generated image:

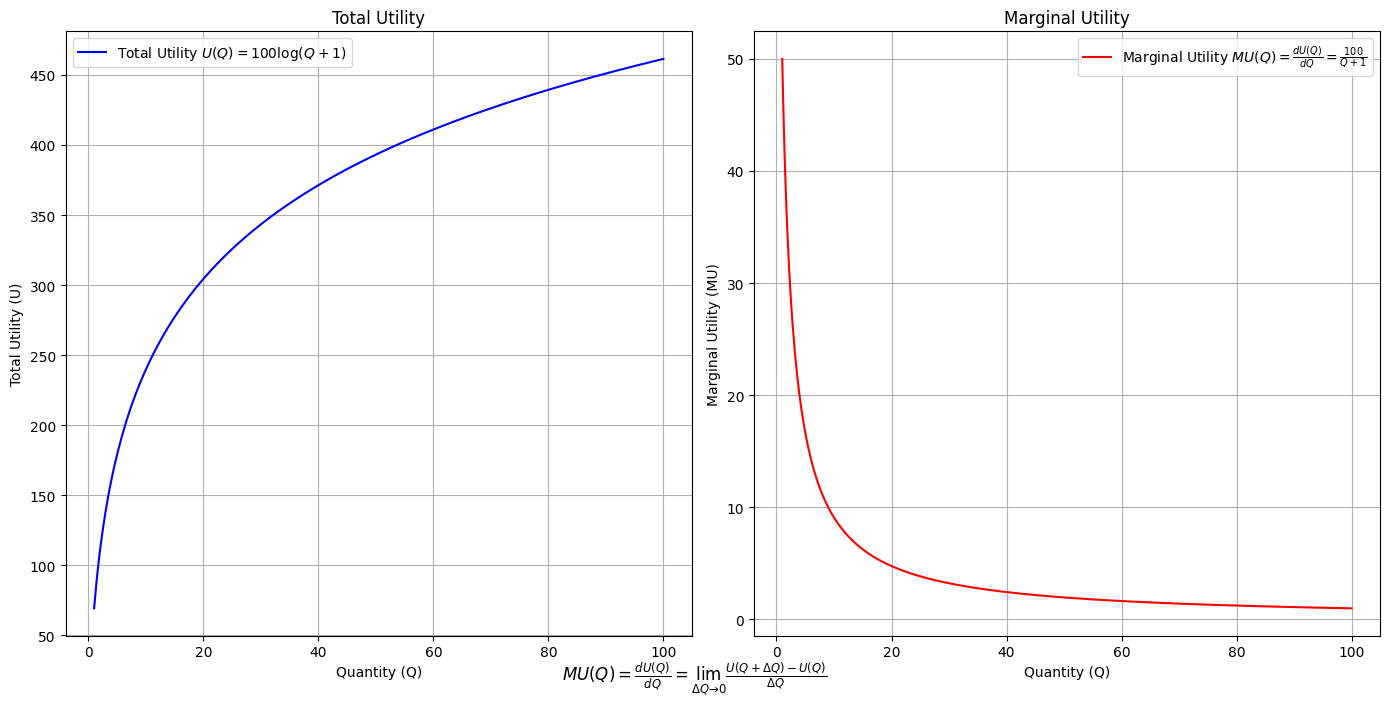
Diminishing Marginal Utility

One needs challenges, a worthy adversary, the embrace of more remote overtones of the harmonic series - Qualities

  • Westmalle Dubbel, \(7\) %

  • Duvel, \(8.5\) %

  • Truth, \(8.7\) %

  • Westmalle Tripel, \(9.5\) %

  • St. Bernardus Abt 12, \(10\) %

Contents